图像信号分析基础

图像信号的数学表示

像素的邻域和邻接

邻域分类：

• 4-邻域 N4(p) 象素p(x,y)的左右上下4个像素。
• D-邻域 ND(p) 象素p(x, y)的4个对角邻近像素。
• 8-邻域 N8(p) 象素p(x, y)的左、右、上、下、左上、右上、左下、右下8个像素。

象素的邻接

• 定义:
  1.若 q∈N4(p)或者p∈N4(q) 则称p与q 4-邻接
  2.若 q∈N8(p)或者p∈N8(q) 则称p与q 8-邻接
• 关系: 4-邻接必8-邻接,反之不然

像素间的连通性



距离度量

图像的运算

算术和逻辑运算

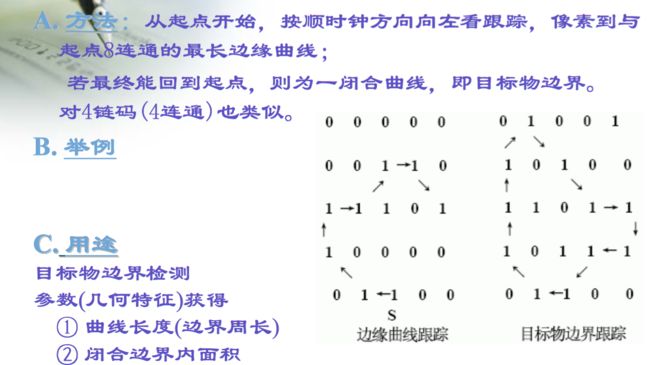
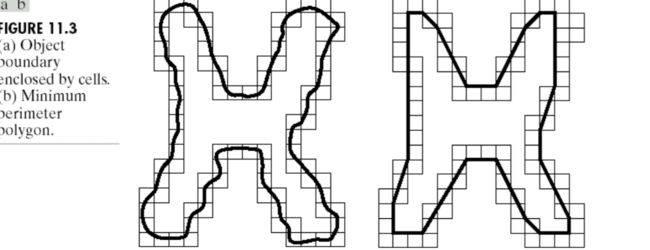
图像中目标物边缘(边界)往往是一种闭合曲线。在数字图象中,线条或边界是一串由离散像素点组成(如下图)。

若用一网络覆盖图像,并是像素点位于网络的交点上,则表示数字图象的线条可看作是由短的线段组成的链。这些短的线段正好是相邻交点的连线。这样就可以用链码来描述任意曲线或闭合的边界。

边界的形状数表示

边缘线(边界)的链码跟踪——以8链码为例

线性系统

系统

从形式上看,系统的功能是 施行一种运算,它把一个 信号(输入)映射成另一个信号(输出)。如果把体现这种运算的映射函数记为 T[·] ,则有 y=T[x] .

式中的映射函数 T[·] 表示:输入信号映射成输出信号的一种(或一组)规则,或者一个对应表格。

对于图像处理系统,输入和输出都是二维信号,映射 函数T[·]是二维函数。

线性系统的性质

一个系统是线性系统的充分必要条件:

同时满足叠加原理与齐次原理。
叠加原理:如果输入信号是两个序列之和,则输出信号也为两 个对应的输出信号之和。
若 y1=T[x1],y2=T[x2] ,则有 y1+y2=T[x1]+T[x2]。

齐次原理:如果 y=T[x] y=T[x],则有 ay=T[ax]=aT[x] 。

综合上述两个原理,线性系统对于所有输入信号 x1,x2 以及所有 复常数a和b,皆有: ay1+by2=T[ax1+bx2]

线性系统服从叠加原理,所以线性系统对于输入信号的加权和的响应等于单个输入信号响应的加权和。

线性平移不变系统

平移不变系统:指如果输入序列进行移位,则输出序列进行相应的移位。

对于二维系统,如果y(i, j)=T[x(i, j)] ,则平移不变条件是: 当且仅当对所有序列 x(i,j) 及所有整数移位 (m,n) ,皆有

y(i−m,j−n)=T[x(i−m,j−n)]
系统的 平移不变和 线性是两个独立的特性,一个特性成立 并不意味着另一个特性也一定成立。

E.g.系统 T[x(i,j)]=[x(i,j)]2 是平移不变的,但不是线性的; 系统 T[x(i,j)]=k(i,j)x(i,j) (其中 k(i,j) 是增益)是线性的,但不是平移不变的。

线性平移不变系统:指既满足线性条件又满足平移不 变条件的系统。

如果对每个 (m,n) 点空间变化冲激响应 hmn(i,j) 则线性系统对任意输入的响应可利用叠加原理求得。
如果系统还是平移不变的,则可进一步简化。

hmn(i,j)≡L[δ(i−m,j−n)]
故在( m=0,n=0 )的特殊情况下,有 h00(i,j)≡L[δ(i,j)] 利用平移不变性质,应有 hmn(i,j)=h00(i−m,j−n)

这样一来,空间变化冲激响应变成了空间不变(坐标原点处)冲激响应的移位序列。若定义 $h(i, j) ≡ h_{00}(i, j),则可把输出序列写成:

g(i,j)=∑∞m=−∞∑∞n=−∞f(i,j)h(i−m,j−n)

1. 一个空间线性平移不变系统的输出就是该系统的空间不变 冲激响应h (i, j)的加权和。而所加的“权”就是系统的输入 f(i, j)。
2. 一个线性平移不变系统完全可以用它的空间不变冲激响应 h(i, j)来表征。
3. 是一个离散二维卷积,i.e. 线性平移不变系统的输出等于 系统的输入与它的空间不变冲激响应的卷积。

二维线性平移不变系统 的频率响应

单位冲激响应为h (i, j)的线性平移不变系统对图像输入的响应
输入信号是复正弦: f(i,j)=exp(jui+jvj)
式中 u,v 是实数,分别称为水平频率(分量)与垂直频率(分量); u,v 后面的 i,j 是坐标值(注意:不要混淆了虚数记号j与位置坐标记号j)
∞∞

输出信号

g(i,j)=∑∞m=−∞∑∞n=−∞h(m,n)exp[ju(i−m)+jv(j−n)]=exp(jui+jvj)[∑∞m=−∞∑∞n=−∞∑h(m,n)exp(−jum−jan)]
g(i,j)=exp(jui+jvj)H(u,v)
输出信号与输入信号有相同频率的复正弦,而它的幅度和相位 则由复增益H(u,v)的影响而产生变化。
系统的频率响应
H(u,v)≡∑∞i=−∞∑∞j=−∞h(i,j)exp(−jui−jaj)

---

图像的卷积计算

卷积积分

卷积(convolution) (积分)是图像处理中十分重要的基本计算法则,就像算术中的四则运算一样。

卷积积分(卷积) :

g(t)=∫∞−∞h(t−τ)f(τ)dτ

h(t)是表征线性平移不变系统特性的一个函数,叫做该系统的冲激响应,是指当系统的输入是单位冲激时得到的输出。线性平移不变系统的输出可通过输入信号与该系统的冲激响应的卷积得到。

卷积积分可以简化为: g=h∗f 。其中运算符合“*”代表前后两个函数的卷积。下图描述了两个函数的卷积过程。卷积积分的结果是图中的阴影部分的 面积,最后的结果g(t)是t的函数。

卷积积分:如果函数 g(t) 满足下列关系式

g(t)=∫∞−∞f(t)h(t−τ)dτ=f(t)∗h(t)

卷积积分的图解表示:

卷积积分的步骤

1. 折迭:把 h(τ) 相对纵轴作出其镜像
2. 位移:把 h(-τ) 移动一个 t 值
3. 相乘:将位移后的函数 h(t-τ) 乘以f(τ)
4. 积分: h(t-τ) 和 f(τ) 乘积曲线下的面积即为 t 时刻的卷积值

卷积积分的性质:

• 交换律 h∗f=f∗h
• 分配律 f∗(l+h)=f∗l+f∗h
• 结合律 (f∗h)∗l=f∗(h∗l)
• 求导
  ddt[f∗g]=dfdt∗h=f∗dhdt

包含脉冲函数的卷积:即 f(t) 或 h(t) 中有一个为脉冲函数 ,则它们的卷积是一种最简单的卷积.

卷积定理:如果 f(t) 和 h(t) 的富里叶变换分别为 f(f) 和 H(f) , 则f(t) * h(t) 的富里叶变换为 H(f)f(f)。即

h(t)∗f(t)⇔H(f)F(f)

卷积定理的简单推导:
∫∞−∞g(t)e−j2πft=∫∞−∞[∫∞−∞f(τ)h(t−τ)dτ]e−j2πftdt=∫∞−∞f(τ)[∫∞−∞h(t−τ)e−j2πftdt]dτ

---

相关

相关积分的计算步骤:

1. 位移:把 h(τ) 移动一个 -t 值
2. 相乘:将位移后的函数 h(t+τ) 乘以 f(τ)
3. 积分: h(t+τ) 和f(τ) 乘积曲线下的面积即为 t 时刻的相关值

相关定理:如果 f(t) 和 h(t) 的富里叶变换分别为 F(f) 和 H(f) ,则 f(t) 和 h(t) 的相关积分为 F(f)H*(f)。即

∫∞−∞h(τ)f(t+τ)dτ⇔H(f)F∗(f)
其中, F∗(f) 为 F(f) 的复共轭

二维卷积

设f和h分别是二元连续函数,即f(x,y)和h(x,y),则它们的卷积积分为

g(x,y)=f∗h=∫∞−∞f(u,v)h(x−u,y−v)dudv

式中的h是一个卷积函数 用在图像处理之中,这个卷积函数就是一个表征图像处理系统性质的函数。

二维连续函数的卷积过程与一维卷积相似,也是 反转-平移-直(点)积-积分的过程。二维 卷积的结果g(x,y)是一个体积。

离散二维卷积的矩阵运算

g(i,j)=∑∞m=−∞∑∞m=−∞f(m,n)h(i−m,j−n)
二维卷积过程如下:

1. 由h(i, j)产生序列h(i-m, j-n)。首先把h(m, n)对 m和n轴进行反转,然后进行平移,使得抽样 h(0, 0)处于(i, j)点上。
2. 计算f(m,n)h(i-m, j-n)乘积序列。
3. 将乘积序列的各非零抽样值相加,得到卷积输出值g(i, j)
4. 当m、n变化时,则序列h(i-m, j-n)移到(m,n)平 面的另一个位置,得到另一个卷积输出值。

二维卷积卷积运算比较复杂,不能用两个二维序列的矩阵形式直接运算。要对它们进行适当的构造以通过矩阵相乘的运算得到卷积的结果。

• 首先认为两个序列 f(i,j) 与 h(i,j) 都是在 x 和 y 方向上周期至少为 N 和 M 的无限长周期序列的一部分。
• 将它们用矩阵形式描述,则为 F 与 H ,它们的卷积为 G=F∗H=H∗F
• 设 F 的大小为 (mf×nf) , H 的大小为 (mh×nh) 。由于卷积运算是两个序列之间展转相乘求和的过程, 所以在运用矩阵形式时要把 F 和 H 加以扩展。扩展 后的矩阵大小为 M×N (其中 M≥mf+mh−1 , N≥nf+nh−1 )用”0”元素填充扩展区的行、列,把扩展后 的矩阵命名为 Fp 和 Hp 。为了方便起见,令 M=N 。

这四个块矩阵分别构成了循环矩阵Hb的第一列。 Hb 的第二列、第三列 和第四列由第一列四个块矩阵的次序循环交换构成。

卷积与滤波

卷积的数字实现可用于对数字信号和数字图像的线性滤波.采样方波信号和滤波器冲激响应的卷积过程如下图所示:

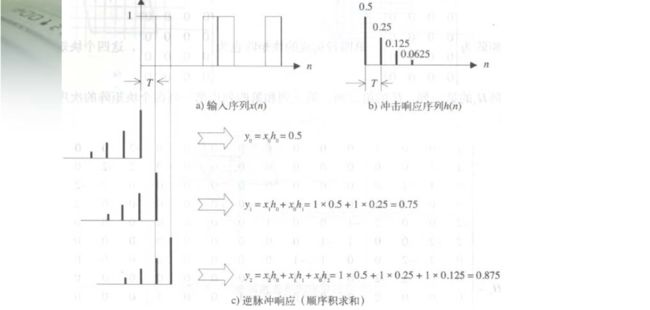
单位脉冲输入通过一个一阶低通滤波器之后,减少了一定的高次谐波

---

卷积的作用和应用

1. 平滑 可采用矩形脉冲、三角脉冲或高斯脉冲为平滑函数。等价于邻域处理中的平滑去噪。
2. 边缘增强带负的旁瓣(side lobes)的正尖峰函数,其边缘增强时产生两个效果。
   
   1. 增加边缘的梯度;
   2. 在边缘的两侧加边。类似与拉普拉斯算 子产生的效果。
3. 去卷积 利用一个卷积去除另一卷积影响的技术。

关于 图像工程基础与实践更多讨论与交流，敬请关注本博客和新浪微博songzi_tea