蓝桥杯C++ AB组辅导课

今天在AcWing闲逛白嫖到了yxc老师的蓝桥杯C++ AB组辅导课的题单，正好快要蓝桥杯了，我准备每天花半个小时刷5道这个题单里的水题，练一练，不然到时候我各种花里胡哨的算法学了一堆，水题切不动就gg了。

一共86道水题，每天5道半个月水完吧

这是蓝桥杯C++ AB组辅导课的链接感兴趣的可以报个名，y老师的课还是很有质量保证的

这个课我就没必要报来听了，刷刷题就好。

第一讲、递归与递推

第一章是递归，我最讨厌的就是递归了。。。

1.AcWing 92. 递归实现指数型枚举

dfs，直接用状态压缩。
dfs就是设置边界，以及当前选或者不选。

void dfs(int num,int state){
    if(num >= n){
        for(int i = 0;i < n;++i)
            if(state >> i &  1)printf("%d ",i + 1);
        puts("");
        return ;
    }
    dfs(num + 1,state);
    dfs(num + 1,state | (1 << num));
}

int main(){
    cin>>n;
    dfs(0,0);
    return 0;
}

2.AcWing 94. 递归实现排列型枚举

可以直接用我很久没用的next_permutation全排列输出

int main(){
    cin>>n;
    for(int i = 1;i <= n;++i)
        a[i] = i;
    do{
        for(int i = 1;i <= n;++i)
            printf("%d ",a[i]);
        puts("");
    }while(next_permutation(a + 1,a + 1 + n));
    return 0;
}

也可以用dfs

void dfs(int num,int state){
    if(num == n){
        for(int i = 0;i < n;++i)
            printf("%d ",a[i]);
        puts("");
        return;
    }
    for(int i = 0;i < n;++i){
        if(state >> i & 1)continue;
        a[num] = i + 1;
        dfs(num + 1,state | (1 << i));
    }
}

int main(){
    scanf("%d",&n);
    dfs(0,0);
    return 0;
}

3.AcWing 1209. 带分数

题目实际上就是 给定一个数N，问有多少组$a,b,c$满足$a+\frac{b}{c}=N$，且$a,b,c$三个数不重不漏地涵盖$1-9$这9个数字，输出总组数。

这里的N的数据范围没有任何实际意义，只是用来判断的。

也就是这道题实际上是一个全排列并且枚举分段判断是否符合该式子。

然后尽量避免使用除法，所以我们化简一下使用乘法即可。

int ans;
int calc(int l,int r){
    int res = 0;
    for(int i = l;i <= r;++i){
        res = res * 10 + a[i];
    }
    return res;
}

void dfs(int num){
    if(num == 9){
        for(int i = 0;i < 7;++i){
            for(int j = i + 1;j < 8;++j){
                int a = calc(0,i);
                int b = calc(i + 1,j);
                int c = calc(j + 1,8);
                if(a * c + b == c * n)ans ++;
            }

        }
        return ;
    }

    for(int i = 1;i <= 9;++i){
        if(vis[i])continue;
        a[num] = i;
        vis[i] = true;
        dfs(num + 1);
        vis[i] = false;
    }
    return ;
}

int main(){
    scanf("%d",&n);
    dfs(0);
    printf("%d\n",ans);
    return 0;
}

第二讲、二分与前缀和

1.AcWing 789. 数的范围

二分模板

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;

const int N = 510007, M = 510007, INF = 0x3f3f3f3f;
int t;
int n,m,k,q;
int dist[N];
bool vis[N];
int ver[M],nex[M],edge[M],head[N],tot;
int cnt;
int a[N],b[N];
int maxx,minn;
int ans;

int main(){
    scanf("%d%d",&n,&q);
    for(int i = 1;i <= n;++i)
        scanf("%d",&a[i]),vis[a[i]] = 1;
    while(q--){
        int x;
        scanf("%d",&x);
        if(!vis[x]){
            puts("-1 -1");
            continue;
        }
        
        int l = 1,r = n;
        while(r > l){
            int mid = l + r >> 1;
            if(a[mid] >= x)r = mid;
            else l = mid + 1;
        }
        printf("%d ",l - 1);
        
        r = n;
        while(r > l){
            int mid = l + r + 1 >> 1;
            if(a[mid] <= x)l = mid;
            else r = mid - 1;
        }
        printf("%d\n",l - 1);
    }
    return 0;
}

2.AcWing 790 .数的三次方根

浮点数二分。
注意数据类型和精度，因为要保留6位小数，所以eps至少也应该设为1e-7，1e-8.

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;

const int N = 510007, M = 510007, INF = 0x3f3f3f3f;

double n;

int main(){
    scanf("%lf",&n);
    double l = -1000,r = 1000;
    while(r - l > 1e-8){
        double mid = (l + r) / 2;
        if(mid * mid * mid > n)
            r = mid;
        else l = mid;
    }
    printf("%.6f\n",l);
    return 0;
}

3.AcWing 730. 机器人跳跃问题

直接二分判断。但是数据比较大，如果1e5个1e5加起来就是1e10会爆int，在check函数里判断一下如果已经大于最大值就直接返回false（已满足E不会小于0），不然再加下去就会爆int变成负数返回true了。

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;

const int N = 510007, M = 510007, INF = 0x3f3f3f3f;

int n;
int h[M];

bool check(int E){
    for(int i = 1;i <= n;++i){
        if(h[i] > E)E -= (h[i] - E);
        else E += (E - h[i]);
        if(E < 0 )return true;
        if(E > 1e5)return false;
    }
    return false;
}


int main(){
    scanf("%d",&n);
    for(int i = 1;i <= n;++i){
        scanf("%d",&h[i]);
    }
    int l = 1,r = 1e5;
    while(r > l){
        int mid = (l + r) >> 1;
        if(check(mid))//如果不够
            l = mid + 1;
        else r = mid;
    }
    printf("%d\n",r);
    return 0;
}

4.AcWing 1205. 买不到的数目

因为一定有解，所以我们可以手算几组数据或者直接打表找规律。

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;

const int N = 510007, M = 510007, INF = 0x3f3f3f3f;

int n;
int h[M];
int x,y;

int main(){
    while(~scanf("%d%d",&x,&y)){
        for(int k = 1000;k >= max(x,y);--k){
            bool flag = 0;
            for(int i = 0 ;i <= 300;++i)
                for(int j = 0;j <= 300;++j)
                    if(i * x + j * y == k)
                            flag = 1;
            if(!flag){
                cout<<k<<endl;
                break;
            }
        }
    }
    return 0;
}

打出来是这个

很明显除去几组失误样例，其他的都是可用的。

我们对x和y加减乘除算一下就发现规律为$x\ast y-x-y$，然后$O(1)$输出即可。

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;

const int N = 510007, M = 510007, INF = 0x3f3f3f3f;

int n;
int h[M];
int x,y;

int main(){
    while(~scanf("%d%d",&x,&y)){
        printf("%d\n",x * y - x - y);
    }
    return 0;
}

5.AcWing 795. 前缀和

int main(){
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;++i)
    scanf("%d",&a[i]), sum[i] = sum[i - 1] + a[i];
    for(int i = 1;i <= m;++i){
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n",sum[r] - sum[l - 1]);
    }
    return 0;
}

6.AcWing 796. 子矩阵的和

#include 
#include 
#include 
#include 
#include 

using namespace std;
const int N = 5007;

int a[N][N];
int sum[N][N];
int n, m, q;

int main(){
    scanf("%d%d%d",&n, &m, &q);
    for(int i = 1;i <= n;++i)
        for(int j = 1;j <= m;++j){
            scanf("%d",&a[i][j]);
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
        }
    while(q -- ){
        int a1, b1, a2, b2;
        scanf("%d%d%d%d",&a1,&b1,&a2,&b2);
        printf("%d\n",sum[a2][b2] - sum[a1 - 1][b2] - sum[a2][b1 - 1] + sum[a1 - 1][b1 - 1]);
      /*sum[a1][b1] ++ ;
        sum[a2 + 1][b2 + 1] ++ ;
        sum[a1][b2 + 1] -- ;
        sum[a2 + 1][b1] -- ;*/
    }
    return 0;
}

7.AcWing 1227 .分巧克力

基础的分木棒二分改编版
二分时要注意好停止的边界，两种二分mid的模板换着用，总有一个可以AC

#include 
#include 
#include 

using namespace std;

const int N = 500007;

int n, k;
int H[N], W[N];

bool check(int mid){
    int res = 0;
    for(int i = 1;i <= n;++i){
        res += (H[i] / mid) * (W[i] / mid);
    }
    return res >= k;
}

int main(){
    cin >> n >> k;
    for(int i = 1;i <= n;++i)
    scanf("%d%d",&H[i], &W[i]);
    
    int l = 0, r = N;
    while(l < r){
        int mid = l + r + 1 >> 1;
        if(check(mid))l = mid;
        else r = mid - 1;
    }
    printf("%d\n",r);
    return 0;
}

8.AcWing 1230. K倍区间⭐

首先本题一看就是要求前缀和。
然后思考如何求k的倍数的区间个数。
首先数据范围1e5，求完前缀和再枚举肯定不行。
所以我们分析，区间和为$sum[r]-sum[l-1]$是k的倍数也就是说$sum[r]-sum[l-1]\%k==0$，展开转化一下得到$sum[r]\%k==sum[l-1]\%k$。
也就是说我们只需要找到$\%k$相等的一对前缀和就是一组答案。那么我们要求总的方案数，我们可以用$cnt$数组记录每一个区间$\%k$值的个数，每次res加上相同值的个数，也就是可以组成的方案数。最后再加上$cnt[0]$，因为区可以是一个数，$cnt[0]$就是没有别人跟它匹配的单个区间个数，也要算上。

#include

using namespace std;
typedef long long ll;
const int N = 500007;

ll a[N];
int n, k;
ll res;
ll sum[N];
ll cnt[N];

int main(){
    scanf("%d%d", &n, &k);
    for(int i = 1;i <= n;++ i)
    scanf("%lld", &a[i]);
    for(int i = 1;i <= n; ++ i){
        sum[i] = (sum[i - 1] + a[i]) % k;
        res += cnt[sum[i]];
        cnt[sum[i]] ++ ;
    }
    printf("%lld\n", res + cnt[0]);
    return 0;
}

第三讲 数学与简单DP

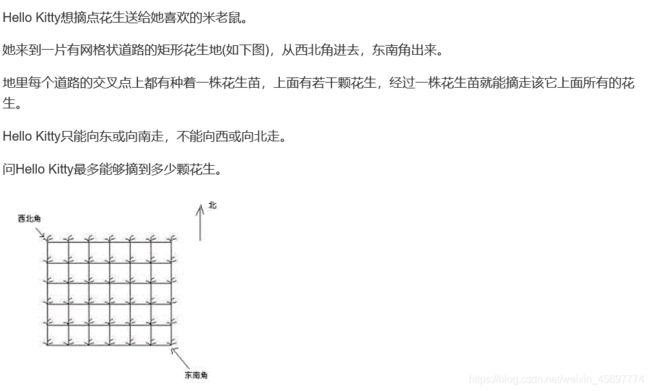
1.AcWing1015. 摘花生

#include
#include
using namespace std;

const int N = 1007;

int n, m, T;
int f[N][N];
int a[N][N];

int main(){
    scanf("%d", &T);
    while(T -- ){
        scanf("%d%d",&n,&m);
        for(int i = 1; i <= n;++i)
            for(int j = 1;j <= m;++j)
            scanf("%d",&a[i][j]);
        for(int i = 1;i <= n;++i)
        for(int j = 1;j <= m;++j){
            f[i][j] = a[i][j];
            if(i > 1)
            f[i][j] = max(f[i][j], f[i - 1][j] + a[i][j]);
            if(j > 1)
            f[i][j] = max(f[i][j], f[i][j - 1] + a[i][j]);
        }
        printf("%d\n", f[n][m]);
    }
    return 0;
}

2.AcWing 895. 最长上升子序列

$O(n^2)$的暴力做法

#include 
#include 
#include 

using namespace std;

const int N = 50007, M = 500007, INF = 0x3f3f3f3f;

int n,m;
int a[N], f[N];

int main(){
    scanf("%d",&n);
    for(int i = 1;i <= n;++i){
        scanf("%d",&a[i]);
    }
    for(int i = 1;i <= n;++i)
    {
        f[i] = 1;
        for(int j = 1;j < i;++j)
            if(a[j] < a[i])
            f[i] = max(f[i], f[j] + 1);
    }
    
    int res = 0;
    for(int i = 1;i <= n;++i)
        res = max(res,f[i]);
    printf("%d\n",res);
    return 0;
}

3.AcWing 2. 01背包问题

#include
#include
#include

using namespace std;

const int N = 50007;

int a[N], n, m, v;
int w[N], val[N];
int f[N];

int main(){
    scanf("%d%d",&n,&v);
    for(int i = 1;i <= n;++i)
    scanf("%d%d",&w[i], &val[i]);
    
    for(int i = n;i; -- i)
        for(int j = v;j >= w[i]; -- j)
            f[j] = max(f[j], f[j - w[i]] + val[i]);
    cout<<f[v]<<endl;
    return 0;
}

4.AcWing 1211. 蚂蚁感冒

也是一道经典的基础题改编的，同样的思考方式，两个蚂蚁对头没有任何影响可以直接当成穿过去了，因为两个都感冒了，没有什么影响。
注意特判，因为我们这里成立的条件就是右边有碰头的蚂蚁左边才会被感染。

#include
#include
using namespace std;

const int N = 507;

int n, m;
int a[N];

int main(){
    scanf("%d", &n);
    for(int i = 1;i <= n;++i)
        scanf("%d",&a[i]);
        
    int right= 0, left = 0, x = a[1];
    for(int i = 2;i <= n;++i){
        if(a[i] > 0 && abs(a[i]) < abs(x))left ++ ;
        if(a[i] < 0 && abs(a[i]) > abs(x))right ++ ;
    }
    if(x > 0 && right == 0 || x < 0 && left == 0)puts("1");
    else printf("%d\n", left + right + 1);
    return 0;
}

AcWing 1216. 饮料换购

#include

using namespace std;

int n;
int res;
int main(){
    cin >> n;
    res = n;
    while(n){
        res += n / 3;
        n = n / 3 + n - n / 3 * 3 ;
        if(n < 3)break;
    }
    cout << res << endl;
    return 0;
}

第四讲 枚举、模拟与排序

1.AcWing 1210. 连号区间数⭐

注意像这种的题目，比如之前那道杨老师的合照队列，都是数据从1到n，也就是说我们可以直接通过枚举1~n来构造整个合法数据。

本题中连续的概念就是说区间里的数经过排序以后可以连续，也就是说如果区间里有3个数3，1，2，我们排序以后为1，2，3，是一个连续区间。因为数据严格处于1~n之间（或者没有这个限制也一样）；
一个很实用很简单的性质：
一个区间数字连续也就是说最大值与最小值的差值是等于区间长度的话。有时候想不起来

我们利用这个性质直接暴力枚举即可

连续值域区间个数(经典题)

#include
#include

using namespace std;
const int N = 500007, INF = 0x3f3f3f3f;

int n;
int a[N];

int main(){
    scanf("%d",&n);
    for(int i = 1;i <= n; ++ i)
    scanf("%d",&a[i]);
    int res = 0;
    
    for(int l = 1;l <= n; ++ l)
    {
        int maxx = - INF, minn = INF;
        for(int r = l;r <= n; ++ r){
            maxx = max(maxx, a[r]);
            minn = min(minn, a[r]);
            if((maxx - minn) == (r - l))res ++ ;
        }
    }
    printf("%d\n",res);
    return 0;
}

2.AcWing 1229. 日期问题

#include
#include
#include

using namespace std;

int months[]={0,31,28,31,30,31,30,31,31,30,31,30,31};
bool check(int year,int month,int day)
{
    if(!month||month>12||!day)return false;
    else if(month!=2&&day>months[month])return false;
    else if(month==2)
        {
            int heap=year%400==0||year%100!=0&&year%4==0;
            if(day>28+heap)return false;
        }
    return true;
}
int main()
{
    int a,b,c;
    scanf("%d/%d/%d",&a,&b,&c);//格式化读入

    int year,month,day;
    for(int i=19600101;i<=20591231;i++)//在指定区间查找
        {
            year=i/10000,month=i%10000/100,day=i%100;
            if(check(year,month,day))
                if(year%100==a&&month==b&&day==c||//年月日
                month==a&&day==b&&year%100==c||//月日年
                day==a&&month==b&&year%100==c)printf("%02d-%02d-%02d\n",year,month,day);//02d不足二位则补0
        }
    return 0;
}

第五讲 树状数组与线段树

1.AcWing 1265. 数星星

本题构造的神奇输入数据使得我们只需要求一下每个点的小于自己x的结点数即可。
直接用树状数组维护一下x坐标即可。

所以我们遇见这种问题，如果没有像这样排好序，我们也应该这样先以y为第一维，然后以x为第二维排序。

#include
#include
#include
#include
#define lowbit(x) (x & -x)
using namespace std;

const int N = 50007;

int tr[N];
int n, m;
int cnt[N];

void modify(int x, int val){
    for(;x <= N; x += lowbit(x)){
        tr[x] += val;
    }
}

int query(int x){
    int res = 0;
    for(;x;x -= lowbit(x))
        res += tr[x];
    return res;
}

int main(){
    scanf("%d", &n);
    for(int i = 1;i <= n; ++ i){
        int x, y;
        scanf("%d%d", &x, &y);
        x ++ ;
        cnt[query(x)] ++ ;
        modify(x, 1);
    }
    for(int i = 0;i < n; ++ i)
        printf("%d\n", cnt[i]);
    return 0;
}

2.AcWing 1270. 数列区间最大值

树状数组

#include
#include
#include
#include

using namespace std;

const int N = 500007;

int n, m;
int a[N];
struct Tree{
    int l, r;
    int sum;
}tr[N * 4];

void pushup(int p){
    tr[p].sum = tr[p << 1].sum + tr[p << 1 | 1].sum;
}

void build(int p, int l, int r){
    tr[p].l = l, tr[p].r = r;
    if(l == r){
        tr[p].sum = a[r];
        return ;
    }
    int mid = l + r >> 1;
    build(p << 1, l, mid);
    build(p << 1 | 1, mid + 1, r);
    pushup(p);
}

void modify(int p, int x, int val){
    if(tr[p].l ==  x && tr[p].r == x){
        tr[p].sum += val;
        return ;
    }
    int mid = tr[p].l + tr[p].r >> 1;
    if(x <= mid)modify(p << 1, x, val);
    else modify(p << 1 | 1, x ,val);
    pushup(p);
}

int query(int p, int l, int r){
    if(tr[p].l >= l && tr[p].r <= r)
        return tr[p].sum;
    int res = 0;
    int mid = tr[p].l + tr[p].r >> 1;
    if(l <= mid)res += query(p << 1, l, r);
    else if(r > mid)res += query(p << 1 | 1, l, r);
    return res;
}

int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1;i <= n; ++ i){
        scanf("%d", &a[i]);
    }
    build(1, 1, n);
    
    for(int i = 1;i <= m ; ++ i){
        int x, y, k;
        scanf("%d%d%d",&k, &x, &y);
        if(x > y)swap(x, y);
        if(k == 0)printf("%d\n", query(1, x, y));
        else modify(1, x, y);
    }
    return 0;
}