4.1 python数据结构之串——概述和基本算法

概述：

字符串（string）简称串，也是一种线性结构。在python中和array差不多，因为py的数组也可以包括各种字符（在C/Java一类的语法中，数组必须是同一种数据类型的元素）。线性结构，有限序列，是主要特点。串其中可以包含各种元素，也是计算机主要处理的一类对象。因此，串的题目涉及的范围很广，可以结合其他算法出题，往往比较有难度。通常，动态规划，双指针，回溯和栈是很重要的工具。

串的存储结构：

其存储结构同线性表一样，也分为顺序存储，即各个字符依次存放在连续的存储单元，以及链式存储，同链表一样，特点是，一个结点可以存储多个字符（一个字符占8位），称为结点的大小，结点大小越大存储密度越大，越小运算处理（插入/删除等）越方便。

串的基本的实现操作包括：赋值，复制，判断相等，串长，串连接，求子串，插入，删除，替换，输出。两种存储结构，实现方式不同，在此不再赘述，并不难写。

串的基本算法：

字符串结合其他算法知识的“高级题目”后面会陆续讲解。本文介绍两个字符串的基础算法理论：循环左移和字符串查找（模式匹配）。

循环左移

问题描述：给定一个字符串S[0...N-1],要求把S的前k个字符移到S的尾部，如把S的字符串“abcded"前面的前两个字符“a”,“b”移到字符串的尾部，得到新字符串“cdefab”，即字符串循环左移k位。算法要求：时间复杂度为O（n）,空间复杂度为O(1)。

暴力移位法，简单粗暴，我们当然不考虑了，时间复杂度为O(KN),空间复杂度为O(1);

三次拷贝法，新建一个数组，分三次拷贝，时间复杂度为O(N),空间复杂度为O(K)；

三次翻转法，类似于矩阵转置，设X='ab', Y='cdef '，X ' = 'ba', Y ' = ' fedc ' , ( X ' Y ' ) ' = ' cdefab ' ，时间复杂度为O(n),空间复杂度为O(1)。

由于python语言的特性，简单按照原理写一个例子，不知是否正确，空间复杂度是否O(1)：

def leftshift(string:str, m:int)-> str:
    n = len(string)
    m %= n
    left = string[:m]
    right = string[m+1:]
    left = left[::-1]
    right = right[::-1]
    result = left + right
    result = result[::-1]

    return result

如果不对就要麻烦一点写了，感觉就不太pythonic，下面用Java实现了一下，好像也不是原地改：

package main.learn;

public class rev {
	private static String reverse(String str){
        char[] chars = str.toCharArray();
        System.out.println(chars);
        int from = 0, to = str.length()-1;
        while(from < to){
            char temp = chars[from];
            chars[from++] = chars[to];
            chars[to--] = temp;
        }
        return String.valueOf(chars);
    }


    public static String leftShift(String str, int k){
        String s1 = str.substring(0,k);
        String s2 = str.substring(k+1,str.length());
        s1 = reverse(s1);
        s2 = reverse(s2);
        String result = s1 + s2;
        result = reverse(result);
        return result;

    }

    public static void main(String[] args) {
        String str = "abcdefghijk";

        String str_leftShift = rev.leftShift(str, 4);

        System.out.println(str_leftShift);
    }

}

字符串查找（模式匹配）

暴力匹配法跳过，我们讨论著名的KMP算法（Knuth-Morris-Pratt算法）。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。

下面的内容来自百度百科，也可以看以下博客：

【经典算法】——KMP，深入讲解next数组的求解

KMP算法最浅显理解——一看就明白

设主串（下文中我们称作T）为：a b a c a a b a c a b a c a b a a b b

模式串（下文中我们称作W）为：a b a c a b

在KMP算法中，对于每一个模式串我们会事先计算出模式串的内部匹配信息，在匹配失败时最大的移动模式串，以减少匹配次数。

理解了上述原理，我们发现KMP的算法是不用回溯的，不走回头路，其重点就是求next数组，next中包含了模式串的局部匹配的信息。

KMP算法的框架是这样的，很好理解，关键是求next数组的方法。

def KMP_Match(s, t):    
    slen = len(s)    
    tlen = len(t)    
    if slen < tlen: 
        return -1       
    i = 0        
    j = 0        
    next_list = [-2 for i in range(len(t))]        
    getNext(t, next_list)  
    while i < slen:            
        if j == -1 or s[i] == t[j]:   # 匹配则继续匹配                
            i = i + 1                
            j = j + 1            
        else:                         # 不匹配，s串不回溯，跳到t串指定位置继续匹配
            j = next_list[j]            
        if j == tlen:                 # t串匹配完全，返回初始位置
            return i - tlen    
    return -1

--------------------------------分割线----------下面深入讲解next数组-----------------------------

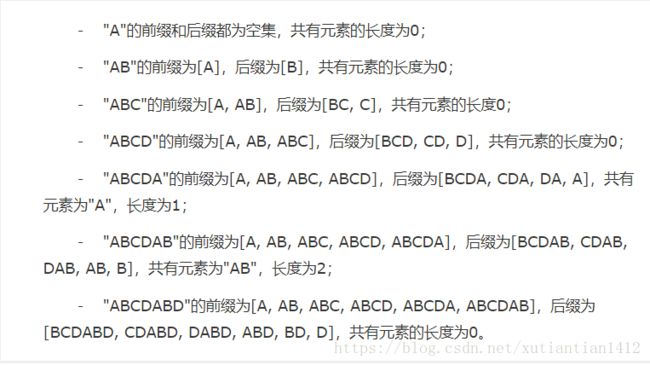
什么叫相同的前缀和后缀呢，以字符串“ABCDABD”为例，看下图：

直接上代码看一下如何求next数组：

def getNext(t, next_list):    
    next_list[0] = -1    
    j = 0        
    k = -1    
    while j < len(t) - 1:        
        if k == -1 or t[j] == t[k]:            
            j = j + 1            
            k = k + 1            
            next_list[j] = k        
        else:            
            k = next_list[k]

如何理解循环内的思想：建议以“ABCDABD”为例自己过一遍代码，next数组中指定了匹配失败跳转到的位置。

不过个人感觉这个求法看起来比较怪异，可以看下面的一个写法，需要注意的是，下面的得到的数组使用方法不同，其得到的是部分匹配表，也就是与前缀相同的后缀的长度。

def get_next(t, next):
    m = len(t)
    next[0] = 0
    k = 0
    for q in range(1, m):
        while k>0 and t[q] != t[k]:
            k = next[k-1]
        if t[q] == t[k]:
            k += 1
        next[q] = k

还是感觉这一部分比较绕，多看几个例子深入理解，靠自己。搞差不多后，建议亲自写一下测试一下。

关于next 数组还有许多变种，以及优化方法，有待后续更新。。。