Matlab:常见涡旋光束仿真
代码:
clc
clear all
close all
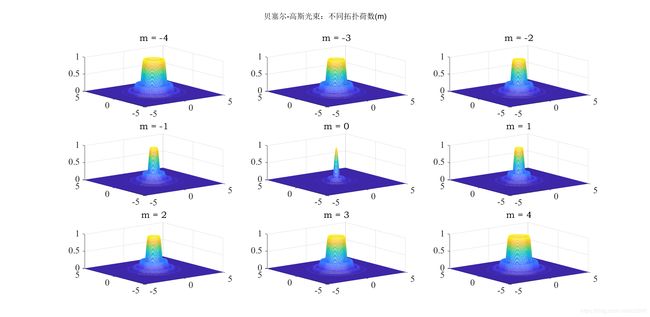
%% 环形涡旋光束
N = 200;
lambda = 632e-9; %波长为632nm
k = 2*pi/lambda; %波数
w0 = 3; %束腰半径
x = linspace(-10,10,N);
y = linspace(-10,10,N);
[X,Y] = meshgrid(x,y);
[theta,r] = cart2pol(X,Y);
beta = 50*pi/180;
figure;
for m = -4 : 4
subplot(3,3,m+5)
E1 = (r/w0).^abs(m).*exp(-r.^2/w0^2)*exp(1i*beta).*exp(-1i*m*theta);
I1 = E1.*conj(E1); I1 = I1/max(max(I1));
%二维
h1 = pcolor(X,Y,I1);
colorbar;
set(h1,'edgecolor','none','facecolor','interp');
title(['m = ',num2str(m)]);
axis square;
% %三维
% mesh(X,Y,I1)
% set(gca,'fontname','times new roman','fontsize',16);
% title(['m = ',num2str(m)],'fontname','华文中宋','fontsize',16);
% %xlabel('x/mm','fontname','times new roman','fontsize',16);
% %ylabel('y/mm','fontname','times new roman','fontsize',16);
% %zlabel('归一化强度','fontname','华文中宋','fontsize',16);
end
suptitle('环形涡旋光束:不同拓扑荷数(m)') %为图一添加总标题
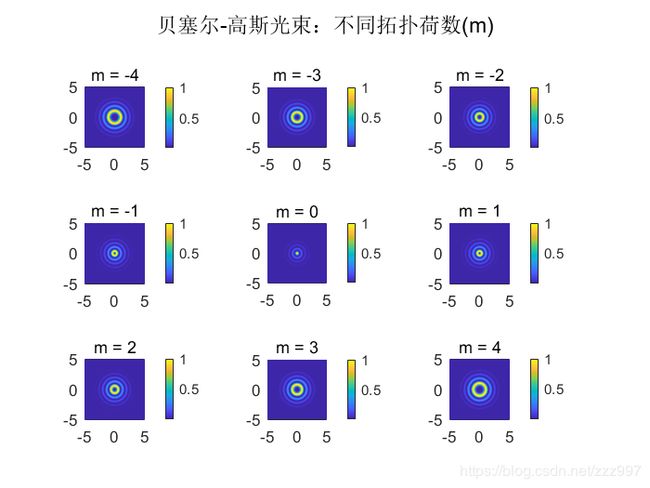
%% 贝塞尔-高斯光束
N = 200;
lambda = 632e-9; %波长为632nm
k = 2*pi/lambda; %波数
w0 = 3; %束腰半径
x = linspace(-5,5,N);
y = linspace(-5,5,N);
[X,Y] = meshgrid(x,y);
[theta,r] = cart2pol(X,Y);
figure;
alpha = 5;
for m = -4 : 4
subplot(3,3,m+5)
E2 = besselj(m,alpha.*r).*exp(-r.^2/w0^2).*exp(-1i*m*theta); %使用了matlab内置的贝塞尔函数
I2 = E2.*conj(E2); I2 = I2/max(max(I2));
%二维
h2 = pcolor(X,Y,I2);
colorbar;
set(h2,'edgecolor','none','facecolor','interp');
title(['m = ',num2str(m)]);
%colormap(gray); %输出灰度图像
axis square;
% %三维
% mesh(X,Y,I2) %三维
% set(gca,'fontname','times new roman','fontsize',16);
% title(['m = ',num2str(m)],'fontname','华文中宋','fontsize',16);
% %xlabel('x/mm','fontname','times new roman','fontsize',16);
% %ylabel('y/mm','fontname','times new roman','fontsize',16);
% %zlabel('归一化强度','fontname','华文中宋','fontsize',16);
end
suptitle('贝塞尔-高斯光束:不同拓扑荷数(m)') %为图二添加总标题
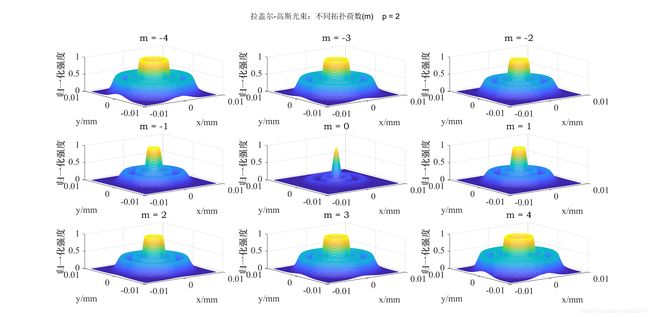
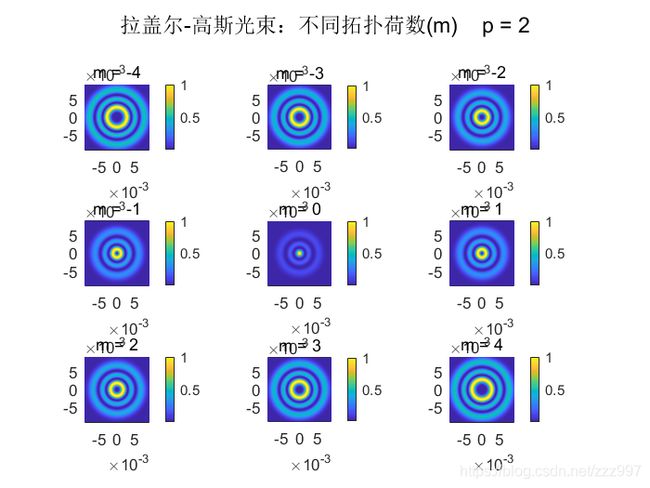
%% 拉盖尔-高斯光束
N = 200;
lambda = 632e-9; %波长为632nm
k = 2*pi/lambda; %波数
w0 = 3e-3; %光斑尺寸
x = linspace(-3*w0,3*w0,N); y = x;
[X,Y] = meshgrid(x,y);
[theta,r] = cart2pol(X,Y);
Z_R = pi*w0^2/lambda; %瑞利长度
z = 0;
w_z = w0*sqrt(1+(z/Z_R)^2);%光束在z位置的半径
figure;
p = 2; %p = 0, 1, 2...;
for m = -4 : 4
subplot(3,3,m+5)
E3 = sqrt(2*factorial(p)/pi/(p+factorial(abs(m))))*(1/w_z)*(sqrt(2)*r/w_z).^abs(m)...
.*exp(-r.^2/w_z^2).*laguerre(p,abs(m),2*r.^2/w_z^2).*exp(-1i*m*theta).*exp(-1i*k*z)...
.*exp(-1i*k*r.^2*z/2/(z^2+Z_R^2))*exp(-1i*(2*p+abs(m)+1)*atan(z/Z_R));
I3 = E3.*conj(E3); I3 = I3/max(max(I3));
% %二维
% h3 = pcolor(X,Y,I3);
% colorbar;
% set(h3,'edgecolor','none','facecolor','interp');
% title(['m = ',num2str(m)]);
% %colormap(gray); %输出灰度图像
% axis square;
%三维
mesh(X,Y,I3) %三维
set(gca,'fontname','times new roman','fontsize',16);
title(['m = ',num2str(m)],'fontname','华文中宋','fontsize',16);
xlabel('x/mm','fontname','times new roman','fontsize',16);
ylabel('y/mm','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);
end
suptitle(['拉盖尔-高斯光束:不同拓扑荷数(m) p = ',num2str(p)]) %为图三添加总标题
%% 拉盖尔多项式(文献5中的公式)
function result = laguerre(p,l,x)
result = 0;
if p == 0
result = 1;
elseif p == 1
result = 1+abs(l)-x;
else
result = (1/p)*((2*p+l-1-x).*laguerre(p-1,abs(l),x)-(p+l-1)*laguerre(p-2,abs(l),x));
end
end
运行结果:


代码仅供参考,不保证正确。
参考文献:
[1]宋晓芳. 不同拓扑荷数的涡旋光束衍射特性研究[D]. 山东师范大学, 2015.
[2]徐丽娟. 涡旋光束的产生及特性研究[D]. 浙江大学, 2014.
[3]吕百达. 激光光学:光束描述、传输变换与光腔技术物理[M]. 高等教育出版社, 2003.
[4]赵麒, 白忠臣, 周骅,等. 拉盖尔-高斯光束作用下熔石英温度及应力研究%Research of temperature and thermal stress of fused silica irradiated by Laguerre-Gaussian beam[J]. 激光技术, 2018, 042(001):121-126.
[5]石业娇. 面向Fredholm微分方程的广义拉盖尔多项式求解方法[J]. 湘潭大学自然科学学报, 2018, 040(001):31-35.