二分查找及对应的几道经典题目

二分查找(Binary Search)属于七大查找算法之一，又称折半查找，它的名字很好的体现出了它的基本思想，二分查找主要是针对的是有序存储的数据集合。

假设有一个集合和一个待查找的目标值，每次都通过将目标值和处于集合中间位置的元素比较，将待查找区间收缩为之前区间的一半，比如目标值小于一次二分查找区间的中间值，则下次查找区间就为原区间的左边一半，重复此过程直至找到目标值或者区间被收缩为0.

下面这幅动图就为二分查找的基本过程，也是最简单的一种二分查找。

最开始我们总是维护两个指针，分别指向数组的起始位置和终止位置，这样做是方便找出数组中间位置，然后下次二分查找时，根据比较结果，选择移动left指针还是right指针来缩小数组长度，二分查找的一个最基本框架如下：

def BinarySearch(nums,target):
    left,right = 0,len(nums)-1
    while left<=right:
        mid = left+(right-left)//2 #计算数组中间位置
        if nums[mid] == target:
            return mid #找到并返回
        # 中间元素大于目标值，搜索数组左半部分
        elif nums[mid] > target:
            right = mid - 1
        # 中间元素小于目标值，搜索数组右半部分
        elif nums[mid] < target:
            left = mid + 1
    return -1 #没找到目标值

如果假设数组的长度为n，每次二分查找后数组长度都会缩小至之前的一半，很容易得出二分查找的时间复杂度为$O(log_2n)$，没有利用额外的存储空间，所以空间复杂度为$O(1)$。

下面通过LeetCode上三道明显体现二分查找思想的例题进一步深入了解此算法的思想，这四道题都是以上面框架为基础，只是在题目中添加了一些约束条件，都为medium难度，会给出对应的题号。

来源：力扣（LeetCode）
链接： https://leetcode-cn.com

33. 搜索旋转排序数组

假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

注意：

• 你可以假设数组中不存在重复的元素。
• 你的算法时间复杂度必须是 O(log n) 级别。

这道题的注意中已经明确要求了时间复杂度，这几乎是指定了这道题目要求你用二分查找实现。可是上面说过二分查找是针对有序数组的查找算法，这里就有些矛盾了，但是利用二分查找是完全可行的。

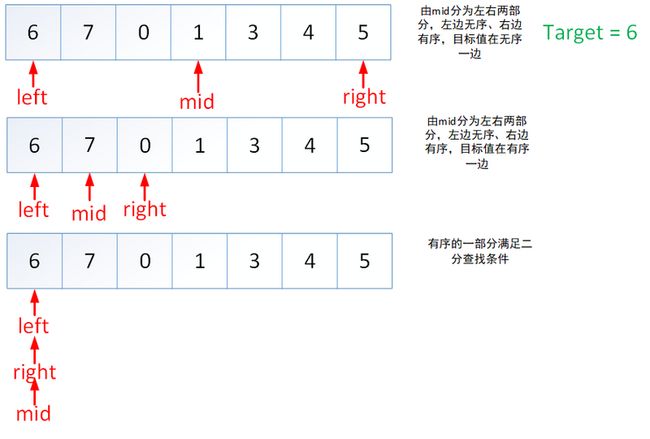
首先需要明确的一个事实是这个数组并不是完全无序，它只是在某个点进行旋转，那么以这个点分隔开的两部分一定是有序的，那它就满足二分查找的条件。在知道这个事实之后，我们可以通过mid指针将数组分为左右两部分，这两部分其中之一必然有序，然后就可以判断出目标值是否存在于有序那部分。

共有两种情况：

• 如果左半部分有序，且目标值位于有序部分中，即$target\in[nums[left],nums[mid])$，下次搜索区间可缩小为$[left,mid-1]$，反之搜索$[mid+1,right]$
• 如果右半部分有序，且目标值位于有序部分中，即$target\in(nums[mid],nums[right])$，下次搜索区间可缩小为$[mid+1,right]$，反之搜索$[left,mid-1]$

有一个帮助理解的key，即使关键值位于无序部分，下次二分查找还是要有上面的划分过程，所以如果目标值存在，那么最后一定是在一部分有序数组中被找到。

def search(nums, target):
    if not nums:  # 空数组
        return -1
    left, right = 0, len(nums) - 1
    while left <= right:
        mid = left + (right - left) // 2
        if nums[mid] == target:
            return mid
        if nums[0] <= nums[mid]:  #左半部分有序
            # 先判断目标值是否存在有序的半个数组中
            if nums[0] <= target < nums[mid]: 
                right = mid - 1
            else:
                left = mid + 1
        elif nums[0] > nums[mid]: #右半部分有序
            if nums[mid] < target <= nums[-1]:
                left = mid + 1
            else:
                right = mid - 1
    return -1

34. 在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

注意:

• 你的算法时间复杂度必须是 O(log n) 级别。
• 如果数组中不存在目标值，返回 [-1, -1]。

同样要求时间复杂度为O(log n)，所以优先考虑二分查找，可以看到这道题要返回的是一个范围，先看示例一，如果只要求返回target的下标，那两个8会返回哪一个呢？我测试了一下，示例一中这种情况是会返回4，也就是第二个8的下标；但如果删去一个7，返回的是2，也就是第一个8的下标，所以返回数组中有重复元素的下标与数组长度有很大关系。

这里就要用到二分查找关于收缩边界的知识，也就是能固定返回数组中重复元素最左边的一个或者最右边的一个，不再受数组长度的影响，所以只要找到目标值左侧边界和右侧边界就可以得到答案。

这里介绍一下左侧边界，右侧类比。与普通框架不同的是，在找到目标时不返回，因为此时找到的目标值不一定就是最左边的一个，这时要收缩右侧边界，以便找到左侧边界，如果left指针和right指针相邻，mid是一定指向left的，所以最后返回left即可，可以根据下面代码推导一下示例一更容易理解。

def searchRange(nums,target):
    res = [-1,-1]
    if not nums: #空数组
        return res
    def leftbound(nums,target): #找到左侧边界
        left,right = 0,len(nums)-1
        while left<=right:
            mid = left + (right-left)//2
            if nums[mid]>target:
                right = mid-1
            elif nums[mid]=len(nums) or nums[left]!=target):
            return -1
        return left
    def rightbount(nums,target): # 找到右侧边界
        left,right = 0,len(nums)-1
        while left<=right:
            mid = left + (right-left)//2
            if nums[mid]>target:
                right = mid-1
            elif nums[mid]

74. 搜索二维矩阵

编写一个高效的算法来判断$m\times n$矩阵中，是否存在一个目标值。

该矩阵具有如下特性：

• 每行中的整数从左到右按升序排列。
• 每行的第一个整数大于前一行的最后一个整数。

二分查找本来是不适用于二维矩阵的，但是这个矩阵有两个特性，在这两个特性的基础上如果将二维数组的所有元素按照顺序依次存入一个一维数组中，那么这个一维数组就是有序的，因此也满足二分查找的条件。

现在最大的问题就是如何通过新建的一维数组的索引在二维矩阵中找到对应的元素，这里像是在于找规律？我也是从题解piao到的，比如16在一维数组中的下标为6，那么他在二维矩阵中的位置为(6//n,6%n)，刚好为(1,2)。只要了解到这个规律，能准确的在矩阵中找到mid指针对应元素，剩下的就是普通升序数组的二分查找。

def searchMatrix(matrix,target):
    m = len(matrix)#行
    if m == 0:
        return False
    n = len(matrix[0])#列
    left,right = 0,m*n-1
    while left<=right:
        mid = left + (right-left)//2
        row = mid // n #元素在矩阵中的行
        col = mid % n #元素在矩阵中的列
        if matrix[row][col] == target:
            return True
        else:
            if matrix[row][col]>target:
                right = mid - 1
            else:
                left = mid + 1
    return False

二分查找比较难搞的地方就是边缘问题，比如循环条件就有很多种表达方式，有带等于号的，也有不带的，我比较习惯用$left<=right$这一种，是否带等于号又和right指针有关，这里的细节感兴趣可以自己查一下，形式一多就会相互混淆，容易出现越界的问题，所以找一种自己认为好理解的形式，不要随意更改。

关注公众号【奶糖猫】可获取更多精彩好文