机器学习——基础概念二:神经网络技巧
文章目录
- 神经网络技巧
- 神经网络的检验
- 特征标准化
- 选择好特征——Good Feature
- 激励函数
- 过拟合:Overfitting
- 加速神经网络训练
- 处理不均衡数据
- 批标准化——Batch Normalization
- L1/L2正规化
神经网络技巧
神经网络的检验
训练数据:70%
检验数据:30%
这就像平时大量做作业,平时分并不多;考试做题只是少数,但却是占分最重的。对神经网络的基本评价基本上是基于这30%的测试数据。
看一下检验神经网络时参考的曲线:
误差曲线:如果理想的话,刚开始训练误差率降的很快,随后提升的空间减小,曲线也趋于水平。

精确度曲线:最好的精确度是趋近于100%精确。怎样看预测值是连续数字的精确度?可以引用R2分数在测量回归问题的精度;也可以用F1分数,用于测量不均衡数据的精度。

过拟合:我们的学习模型平时的作业做的很好,但考试的时候却考的一团糟。这是为什么呢?神经网络对平时作业过于依赖,考试的时候就不能拓展学到的知识。这就是过拟合啦。解决过拟合也有很多方法,比如L1,L2正规化,Dropout方法。

交叉验证:依然是这个相似的图,纵坐标是误差,但横坐标不是时间而是某一层神经网络的某一参数。逐渐调整这个参数,找到满足误差要求的那个参数就好了。

特征标准化
或称之数据的正常化、归一化。训练的时候数据跨度不一,参数变化对这些数据的影响力不同,会导致不同类型数据的训练速度不一。
通常用于特征标准化的途径有两种:
- MinMax Normalization。将所有特征数据按照比例缩放到0-1这个取值区间,有时候也可以是-1到1的区间。
- Standard Deviation Normalization。用均值、方差进行标准化。
选择好特征——Good Feature
- 避免无意义的信息
排除掉没有区分能力的信息,用更多有意义的信息来综合判断当作判断依据。 - 避免重复的信息
比如描述距离,里和公里虽然是不同的信息,但是对机器学习并没有帮助 - 避免复杂的信息
比如描述两个位置的关系,分别有两种信息,经纬度和距离。显然经纬度会更加复杂,不适合描述。
激励函数
Linear,线性方程
Nonlinear,非线性方程
激励函数:用来解决不能用线性方程概括的问题。将线性函数强行“掰弯”,也就是将线性函数作为参数带入到激励函数中。激励函数必须是可微分的,可谓分的激励函数才能将误差反向传递回去。
在少量层结构中,我们可以选择尝试很多种不同的激励函数。
CNN中,推荐relu
RNN中,推荐tanh或者relu。
过拟合:Overfitting
学习模型过于自信,过于依赖训练数据。不能表达训练数据以外的数据。比如这张图片,训练的时候能很准确区分出两者的界限,但是实际操练的时候,由于原有模型过于依赖训练数据,发生了区分失误。

解决方法:
-
增加数据量
-
运用正规化:L1,L2…regularization。把W参数自身调整到误差值中,促进让神经网络调小这个值。
Y = W x L 1 : c o s t = ( W x − r e a l y ) 2 + a b s ( W ) L 2 : c o s t = ( W x − r e a l y ) 2 + W 2 L 2 : c o s t = ( W x − r e a l y ) 2 + W 2 L 3 , L 4...... Y=Wx\\ L1: cost = (Wx - real y)^2 + abs(W)\\ L2: cost = (Wx - real y)^2 + W^2\\ L2: cost = (Wx - real y)^2 + W^2\\ L3, L4...... Y=WxL1:cost=(Wx−realy)2+abs(W)L2:cost=(Wx−realy)2+W2L2:cost=(Wx−realy)2+W2L3,L4...... -
Dropout regularization:训练的时候,随机忽略掉一些神经元和神经连接,让神经网络不完整,用一个不完整的神经网络训练一次。第二次的时候再随机忽略一些,变成另外一个不完整的神经网络。这样的话,神经网络从根本上没有机会过度依赖某些神经元、某些参数。
加速神经网络训练
SGD:Stochastic Gradient Descent。将数据分批交给模型训练,每次训练的数据虽然不能反映整体上数据的特征,但是却提升了训练的速度。

传统方法是再原始W累加上一个负的学习率乘以校正值:
W + = − L e a r n i n g R a t e ∗ d x W += -LearningRate*dx W+=−LearningRate∗dx这种方法会让训练过程曲折无比。
Momentum:
W + = b 1 ∗ m − L e a r n i n g R a t e ∗ d x W+=b1*m-LearningRate*dx W+=b1∗m−LearningRate∗dx相当于给模型一个向下的惯性,让它走的更快。
AdaGrad:
这种方法是在学习率上动手脚,每一个参数的更新都会有自己与众不同的学习率。 v + = d x 2 W + = − L e a r n i n g R a t e ∗ d x / v v+=dx^2\\ W+=-LearningRate*dx/\sqrt{v} v+=dx2W+=−LearningRate∗dx/v这种方法大概理解为,一旦误差dx变大,那么就强制让W的更新减小。
RMSProp:
同时具备上面两种的优势
v = b 1 ∗ v + ( 1 − b 1 ) ∗ d x 2 W + = − L e a r n i n g R a t e ∗ d x / v v=b1*v+(1-b1)*dx^2\\ W+=-LearningRate*dx/\sqrt{v} v=b1∗v+(1−b1)∗dx2W+=−LearningRate∗dx/v也是dx变大,那么就让W除以一个更大的数。
Adam:
m = b 1 ∗ m + ( 1 − b 1 ) ∗ d x v = b 2 ∗ v + ( 1 − b 2 ) ∗ d x 2 W + = − L e a r n i n g R a t e ∗ m / v m=b1*m+(1-b1)*dx\\ v=b2*v+(1-b2)*dx^2\\ W+=-LearningRate*m/\sqrt{v} m=b1∗m+(1−b1)∗dxv=b2∗v+(1−b2)∗dx2W+=−LearningRate∗m/vm有Momentum下坡的属性,v有Adagrad阻力的属性。大多数时候,Adam都能又快又好达成目标,迅速收敛。
处理不均衡数据
一般来说,机器和我们都会猜测比例多的数据。如何获得更高的准确性?
-
想办法获取更多数据
-
换个评判方式
普通评判方式都是
- Accuracy:准确率
- Cost:误差
在不均衡数据面前,前两种评判方式没那么重要。
- Confusion Matrix
- Precision & Recall
- F1 Score -
重组数据
重新组合不均衡数据,使之均衡。- 方式1:复制或者合并少数样本,使之和多数部分数量差不多。
- 方式2: 砍掉一些多数部分,使两者数量相差不多。
-
使用其他机器学习方法
如果使用的机器学习方法,像神经网络等,面对不均衡护具束手无策。不过有些机器学习方法,比如决策树,decision trees就不会受其影响。
-
修改算法
批标准化——Batch Normalization
具有统一规格的数据更有利于机器的学习。
如果数据范围差过大,就如下图的红色部分,有可能就到达了激励函数的不敏感区域,不利于数据分析。
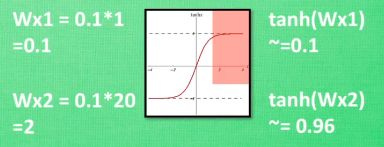
进行BN操作,让数据分布于激励函数的有效区间。训练得到的效果也会更好,结果不会是分布于参数的两个极端。


BN算法:
Input: Values: B = { x 1 , x 2 , . . . x m } B=\{x_1,x_2,...x_m\} B={x1,x2,...xm}.
Parameters to be learnt: γ , β \gamma , \beta γ,β
Output: { y i = B N γ , β ( x i ) } \{y_i = BN_{\gamma, \beta }(x_i)\} {yi=BNγ,β(xi)}
μ β = ∑ i = 1 m x i m \mu_\beta = \frac{\sum_{i=1}^{m}x_i}{m} μβ=m∑i=1mxi
σ 2 = 1 m ∑ i = 1 m ( x i − μ β ) 2 \sigma^2 = \frac{1}{m}\sum_{i=1}^{m}(x_i-\mu_\beta)^2 σ2=m1i=1∑m(xi−μβ)2
x i ^ = x i − μ β σ 2 + ϵ \hat{x_i}=\frac{x_i-\mu_\beta}{\sqrt{\sigma^2+\epsilon}} xi^=σ2+ϵxi−μβ
y i = γ x i ^ + β = B N γ , β ( x i ) y_i = \gamma \hat{x_i}+\beta = BN_{\gamma, \beta}(x_i) yi=γxi^+β=BNγ,β(xi)
看到了概率论中的知识了!在学校的理论课没白学。
公式的最后一行是反向操作,将normalized数据再扩展、平移。让神经网络自己学着使用和修改这个扩展参数 γ \gamma γ和平移参数 β \beta β。
L1/L2正规化
解决过拟合的问题。过拟合,就如同下图中的橙色曲线。希望得到的结果是:a,b,c,d都是待计算的参数,到最后c和d都是0.

L2正规化:
误 差 : J ( θ ) = [ y θ ( x ) − y ] 2 + [ θ 1 2 + θ 2 2 + . ] 误差:J ( \theta ) = \left[ y _ { \theta } ( x ) - y \right] ^ { 2 } + \left[ \theta _ { 1 } ^ { 2 } + \theta _ { 2 } ^ { 2 } + . \right] 误差:J(θ)=[yθ(x)−y]2+[θ12+θ22+.]
L1正规化:
误 差 : J ( θ ) = [ y θ ( x ) − y ] 2 + [ ∣ θ 1 ∣ + ∣ θ 2 ∣ . . ] 误差:J ( \theta ) = \left[ y _ { \theta } ( x ) - y \right] ^ { 2 } + \left[ \left| \theta _ { 1 } \right| + \left| \theta _ { 2 } \right| . . \right] 误差:J(θ)=[yθ(x)−y]2+[∣θ1∣+∣θ2∣..]
这里的 θ \theta θ就相当于上面的abcd这些参数。当当图像出现过拟合的时候,也就是c和d过大, θ 3 , θ 4 \theta_3, \theta_4 θ3,θ4过大了。
下图:假如有两个参数 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2需要学习。蓝色的圆心是误差最小的地方,每条蓝线的误差都是一样的。正规化的方程在黄线上产生的的额外误差,黄线上的误差也是一样。黄线和蓝线上的交点处,两个误差的和最小。
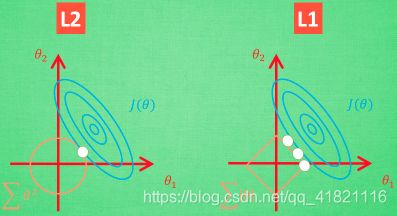
L1可能只能保留 θ 1 的 特 征 , \theta_1的特征, θ1的特征,另外就是L1的解并不稳定,就如同上图右侧,黄蓝图像的交点有好多个。
对L1、L2规范化还是有些不明白,后续补上自己的理解。
插个眼:L1L2规范化解释
第一次编辑:2019-05-11 17:19:36