模拟调制

通信原理专题目录

在傅里叶变换的应用之调制解调中，也讲到过调制解调，但这远远不够，这里正式介绍模拟调制，且多从时域方面来理解。

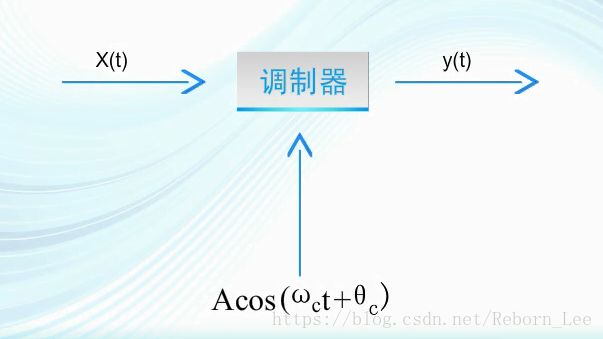
调制的基本模型如下：

用信号x（t）去控制载波的某一个参数，使得这个参数安装信号x(t)的规律来变化；

那载波有哪些参数可控制呢？

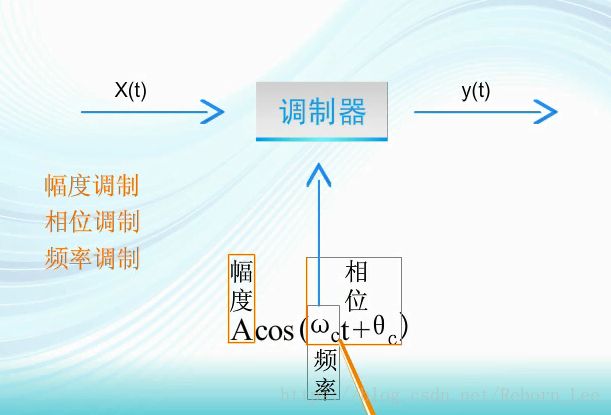
x(t)怎么去控制载波的幅度、相位和频率呢？

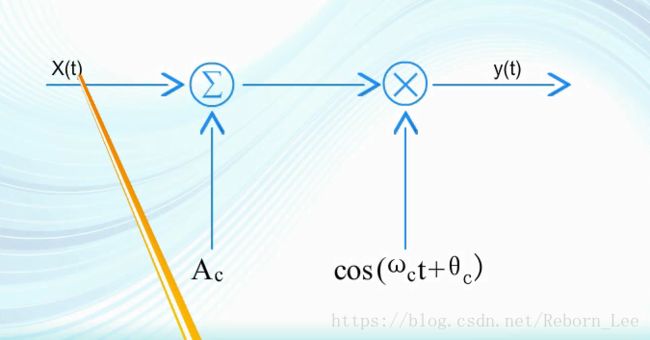
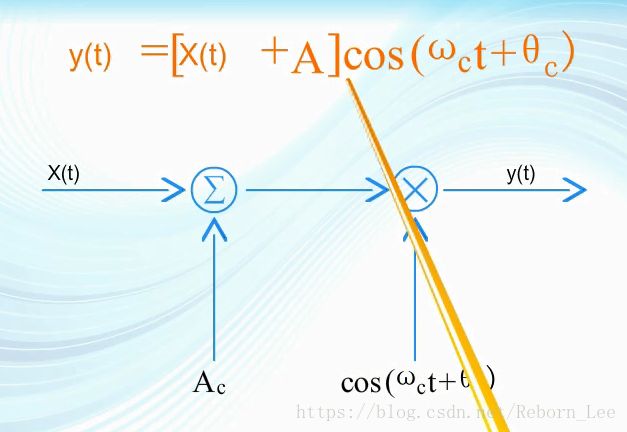
一般是将x(t)加在这些参数之中，比如，拿调幅来说：调制信号先与载波的最大振幅相加，再与载波相乘，那么载波的幅度就随x(t)而变化了。

这个调制电路的实现模型就是一个加法运算和乘法运算：

而要控制相位和频率，同样需要在载波的相位和频率处添加x(t)的影响，如调相信号，载波的相位中多了X(t)，即载波的相位随x(t)线性的变化。

调频信号中，载波的相位随x(t)的积分线性变化。

模拟的调相和调频电路的实现比调幅电路稍微复杂一点，不过现在主要应用的是数字调制，因此我们要重点关注的是数字调制，数字调制后面会有独立博文讲解。

下面通过模拟调幅信号的解调原理，认识一下相干解调以及非相干解调。

相干是什么意思呢？

为简单其间，我们假设调制信号是一个单一信号，波形图如下：

假设载波信号的最大振幅是1，则1+x(t)如下图：

载波信号的波形图如下：

已调信号的波形图：（注意，下面图中的纵坐标的表达式书写错误，应该是 ）

从上图可以看出，已调信号的包络形状其实就是调制信号的波形图，这样在解调时，就可以利用包络信息来恢复原始信号x(t)。

这种解调方式叫做包络检波法。

还有一种解调方法是在接收端用一个与载波信号同频、同相的载波与已调信号相乘，

我们来看看相乘后是什么结果：

由于后面的一项未携带有用信息，因此可以将其抑制掉；（如何抑制？）

现在将y(t)与本地载波  相乘，经过积化和差可得如下式子：

积化和差公式：

经过低通滤波器滤掉高频分量 后，得到：

当 为常数时，也就是相位同步时，

可见只有当本地载波与已调信号载波频率相同，且相位同步时，信号才能正确的恢复，否则将会失真。

这种解调方法就叫相干解调。

除此之外的解调叫非相干解调，像前面说的包络检波就是非相干解调。还有一种叫载波插入的解调方法，都是非相干解调的例子。相干解调要比非相干解调效果好，但是复杂度相应也就高一些。