信号与系统-语音信号的调制解调
1 三角波的matlab谐波叠加和当信号周期和宽度变化时的频谱变化
t=-3:0.001:3;
omega=2*pi/2;
y=(sawtooth(2*pi*0.5*(t+1),0.5)+1)/2;
plot(t,y);
grid on;
xlabel('t'),ylabel('三角波');
axis([-3 3 -1.5 1.5])
n_max=[1 3 5 11 47];
N=length(n_max);
for k=1:N
n=1:2: n_max(k);
b=4./(pi^2*n.^2;
x=b*cos(omega*n'*t) + 0.5;
figure;
plot(t,y,'b');
hold on;
plot(t,x,'r');
hold of;
xlabel('t'),ylabel('谐波');
axis([-3 3 -1.5 1.5]);
grid on;
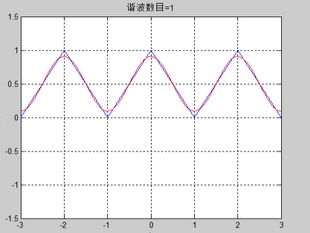
title(['谐波数目=',num2str(n_max(k))]) ;
end
(2. 程序内容:
n=-30:30;
tao=1;
T=10;
w1=2*pi/T;
x=n*tao/T;
fn=2*tao*sinc(x).^2/T;
subplot(311) ;
stem(n*w1,fn),grid on;
title('tao=1,T=10');
tao=1;
T=5;
w2=2*pi/T;
x=n*tao/T;f
n=2*tao*sinc(x).^2/T;
m=round(30*w1/w2);
n1=-m:m;
fn=fn(30-m+1:30+m+1);
subplot(312) ;
stem(n1*w2,fn),grid on;
title('tao=1,T=5');
tao=2;
T=10;
w3=2*pi/T;
x=n*tao/T;
fn=2*tao*sinc(x).^2/T;
subplot(313) ;
stem(n*w3,fn),grid on;
title('tao=2,T=10');
2 载波为简单正弦信号的幅度调制和相干解调
(1.程序内容:
Clc
clear
ts=0.0001;
t= -0.1:ts:0.1;
mt=sin(2*pi*20*t);
A0=2;
uc=sin(2*pi*800*t);
st=(A0+mt).*uc;
subplot(311);
plot(t,mt);
title('sin signal');
subplot(312);
plot(t,uc);
title('carry')
subplot(313);
plot(t,st),grid on;
title('AM')
m0 = uc.*st;
fs=20000;
[N,Wn]=buttord(2*pi*200*2/fs,2*pi*400*2/fs,3,20,'s');
[B,A]=butter(N,Wn,'low');
figure(2);
m1=filtfilt(B,A,m0);
subplot(211);
plot(t,m0),grid on;
title(‘通过乘法器’);
subplot(212);
plot(t,m1),grid on;
title('解调');
在本次试验中,首先我把三角函数表达出来后进行傅里叶级数展开并用不同次数的谐波进行逼近,可以看出次数越多与原来信号的相似程度越高,证明了傅里叶展开的原理与可靠性;然后我们实验了对信号进行了调制与解调的过程。信号的调制与解调的过程实际上就是将想要传输的信号加到载波信号中,并用某种特定的方法再将想要传输的信号从调制后的信号中与载波信号分离开来,这就是信号的调制与解调的大致含义。在实验中我采用正弦信号为载波信号,观察解调后的信号的大体形态与正弦信号相同,验证了调制解调的原理