Python量化交易笔记---16.方差分析

方差分析是一种多变量之间关系的定性分析方法，通过研究多个变量之间存在的关系，我们可以提高预测的准确性。

1.概述

在股票研究中，我们经常按行业版块来进行研究，假设不同行业间收益率为相互独立的，我们想要知道化工行业与金融行业相比，收益率是高还是低。在这个问题中，行业版块我们称之为因子（Factor）变量，因子变量可以取实数值，也可以取如行业类型这样离散状态值，我们称之为水平；我们研究的收益率称之为反应变量。

采用方差分析来解决这类问题时，我们首先从反应变量的方差入手，研究诸多因子变量，哪些因子变量对反应变量有显著的影响。方差分析不能直接用于预测，但是可以识别出重要的因子。

方差分析分为单因素方差分析、多因素方差分析、析因方差分析。多因素方差分析是研究多个因子变量分别对反应变量的影响，而不是这些因素的总体对反应变量的影响。析因方差分析与多因素方差分析相似，就是增加某些因子的乘项。

2.数学原理

2.1.离差平方和

我们假设因子变量$X$共有M个水平，每个水平下观测到的样本数为$N_j,j\in \{1,2,3,...,M\}$，令$Y_{ij}$代表在第$j$个水平组别下第$i$个反应变量的值，其中$i\in \{1,2,3,...,N_j\}$。令${\mu }_j$表示第$j$个水平下反应变量的均值，${\mu }_0$为所有样本的反应变量均值。

我们以研究的股票问题为例，我们要研究的行业为：化工、通信、机械、电子、金融，则M=5，我们有这些行业一年的收益率数据，则$N_j=255$，则$Y_{100,2}$，则代表在第100天通信行业的收益率数据。则${\mu }_2$代表电信行业收益率的均值，${\mu }_0$代表这5个行总体收益率均值。

我们的假设$H_0$为：

$${\mu }_1={\mu }_2=...={\mu }_M={\mu }_0$$

假设用$y_{i,j},j=1,2,3,...,M,i=1,2,3,...,N_j$，则第$j$个水平的均值为：

$$\overline{y_j}=\frac{y_{1,j}+y_{2,j}+...+y_{N_j,j}}{N_j}=\frac{1}{N_j}\sum _{i=1}^{N_j}{y}_{i,j},j=1,2,3,...,M$$

所有水平的反应变量均值为：

$$\begin{gathered} \bar{y}=\frac{1}{N}\sum _{j=1}^M\sum _{i=1}^{N_j}{y}_{i,j} \\ =\frac{1}{N}\sum _{j=1}^M{N}_j\left(\frac{1}{N_j}\sum _{i=1}^{N_j}{y}_{i,j}\right) \\ =\frac{1}{N}\sum _{j=1}^M{N}_j\overline{y_j} \end{gathered}$$

式中$N={\sum }_{j=1}^M{N}_j$为全样本数。根据我们的假设，我们主要是想检验$\bar{y}$与$\overline{y_j}$是否相等。

任意一个样本与全样本均值之间的偏差可以表示为：

$$y_{i,j}-\bar{y}=y_{i,j}-\overline{y_j}+\overline{y_j}-\bar{y}$$

上式中第一项称之为组内偏差，第二项称之为组间偏差。

总离差平方合（Total Sum of Squares, TSS）定义为：

$$\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\bar{y}{)}^2=\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\overline{y_j}{)}^2+\sum _{j=1}^M\sum _{i=1}^{N_j}(\overline{y_j}-\bar{y}{)}^2+2\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\overline{y_j})(\overline{y_j}-\bar{y})$$

对于上式最后一项，$\overline{y_j}-\bar{y}$相当于常数项可以提出对$i$的累加，又因为${\sum }_{i=1}^{N_j}(y_{i,j}-\overline{y_j})={\sum }_{i=1}^{N_j}{y}_{i,j}-N_j\overline{y_j}$的值为0，所以最后一项的值为0，上式可以化简为：

$$\begin{gathered} \sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\bar{y}{)}^2=\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\overline{y_j}{)}^2+\sum _{j=1}^M\sum _{i=1}^{N_j}(\overline{y_j}-\bar{y}{)}^2 \\ =\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\overline{y_j}{)}^2+\sum _{j=1}^M{N}_j(\overline{y_j}-\bar{y}{)}^2 \end{gathered}$$

上式右侧第一项为误差平方和（Error Sum of Squares, ESS），表征组内偏差平方和；第二项为因子平方和（Factor Sum of Squares, ESS），表征组间偏差平方和。

2.2.自由度

自由度是指当以样本的统计量来估计样本的总体参数时，样本中能够独立或自由变动的样本个数。假设一个样本集$x_i,i=1,2,3,...,n$，均值统计量定义为：

$$\bar{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$$

此时，如果我们固定$\bar{x}$，如果$x_1,x_2,...,x_{n-1}$固定后，$x_n$可由下式计算得到：

$$x_n=n\bar{x}-x_1-x_2-...-x_{n-1}$$

因此我们说这个样本集的自由度为$n-1$。

再来看我们的方差定义：

$$S=\frac{1}{自由度}\sum _{i=1}^n(x_i-\bar{x}{)}^2=\frac{1}{n-1}\sum _{i=1}^n(x_i-\bar{x}{)}^2$$

因为此时的自由度为$n-1$，所以得到我们熟悉的方差公式。

下面我们来分析上节中的TSS、ESS、FSS的自由度。

2.2.1.TSS自由度

TSS的定义为：

$$\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\bar{y}{)}^2$$

因为$\bar{y}$是总样本的均值，根据上面的讨论，固定$\bar{y}$，则其自由度为$N-1$，有：

$$\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\bar{y})=0$$

2.2.2.FSS自由度

FSS的定义：

$$FSS=\sum _{j=1}^M{N}_j(\overline{y_j}-\bar{y}{)}^2$$

因为：

$$\sum _{j=1}^M(\overline{y_j}-\bar{y})=\sum _{j=1}^M\overline{y_j}-M\bar{y}=0$$

因此其自由度为$M-1$。我们定义平均数组间均方差为：

$$MSF=\frac{FSS}{M-1}=\frac{1}{M-1}\sum _{j=1}^M{N}_j(\overline{y_j}-\bar{y}{)}^2$$

2.2.3.ESS自由度

ESS的定义为：

$$\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\overline{y_j}{)}^2$$

由于：

$$\sum _{i=1}^{N_j}(y_{i,j}-\overline{y_j})=\sum _{i=1}^{N_j}{y}_{i,j}-N_j\overline{y_j}=0,j=1,2,...,M$$

总共减少了$M$个自由度，所以ESS的自由度为$N-M$。我们定义平均数组内均方差为：

$$MSE=\frac{1}{N-M}\sum _{j=1}^M\sum _{i=1}^{N_j}(y_{i,j}-\overline{y_j}{)}^2$$

2.2.4.关系

TSS、ESS、FSS之间自由度的关系为：$N-1=(M-1)+(N-M)$。

2.3.显著性检验

假设第$j$个水平的样本满足：$Y_{i,j}\sim N({\mu }_j,{\sigma }_0^2)$，组间均方差期望为：

$$E(MSF)={\sigma }_0^2+\frac{1}{M-1}\sum _{j=1}^M{N}_j({\mu }_j-{\mu }_0{)}^2$$

组内均方差期望值：

$$E(MSE)={\sigma }_0^2$$

我们的假设$H_0$为：${\mu }_1={\mu }_2=...={\mu }_M={\mu }_0$，则$E(MSF)=E(MSE)={\sigma }_0^2$，我们定义检验的统计量为：

$$\varphi =\frac{MSF}{MSE}=\frac{\frac{FSS}{M-1}}{\frac{ESS}{N-M}}$$

2.4.方差分析步聚

2.4.1.识别因子变量水平

识别出因子变量及其水平，例如对股票收益率按行业进行研究时，就是找出所有的行业。

2.4.2.提出假设

通常我们的假设$H_0$为：${\mu }_1={\mu }_2=...={\mu }_M={\mu }_0$。

2.4.3.计算统计量

计算MSF和MSE，构造统计量：

$$\varphi =\frac{MSF}{MSE}=\frac{\frac{FSS}{M-1}}{\frac{ESS}{N-M}}$$

2.4.4.检验

计算p值，p值大于0.05时接受，否则拒绝原假设。

3.单因素方差分析

行业收益率数据如下所示：

images/c16f001.png

对其进行方差分析的程序如下所示：

import numpy as np
import pandas as pd
from scipy import stats
import statsmodels.stats.anova as anova
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt

def startup():
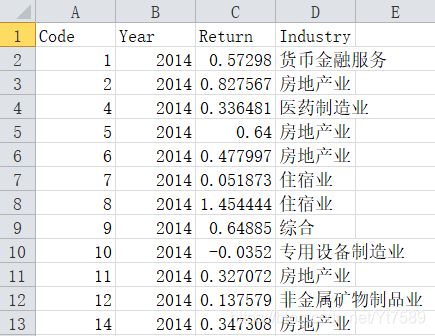
    datas = pd.read_csv('../datas/TRD_Year.csv', encoding='gbk')
    model = ols('Return ~ C(Industry)', data=datas.dropna()).fit()
    rst = anova.anova_lm(model)
    print(rst)
    
if '__main__' == __name__:
    startup()

codes/c16c001.py

其中在第10行中，我们定义因子变量列为C(Industry)，反应变量列为Return。运行结果如下所示：

images/c16f002.png

其p值为4.382045e-28<0.05，因此我们的假设是错误的，即我们认为股票收益率与行业无关的假设是错误的，这与我们的直觉是一致的。

4.多因素方差分析

我们来看1993年美国个人收入数据，如下所示：

images/c16f003.png

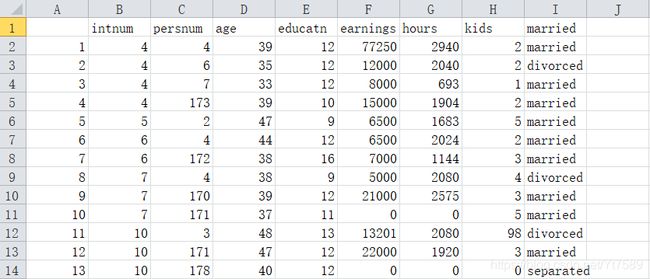
我们要研究的因子变量为E列的教育程度和I列的婚姻状态，而反应变量为F列的收入。

程序如下所示：

import numpy as np
import pandas as pd
from scipy import stats
import statsmodels.stats.anova as anova
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt

def startup():
    psid = pd.read_csv('../datas/PSID.csv')
    model = ols('earnings ~ C(educatn)+C(married)', data=psid.dropna()).fit()
    rst = anova.anova_lm(model)
    print(rst)
    
if '__main__' == __name__:
    startup()

codes/c16c002.py

在第10行我们选择了教育程度和婚姻状况作为因子变量。运行结果如下所示：

images/c16f004.png

由上图可以看出，教育程度对应的p值为6.198294e-190，婚姻状况对应的p值为3.795366e-06，二者均小于0.05，因此可以认为二者均对收入有显著的影响。

5.析因方差分析

还以上一节的例子为例，我们要研究教育程度和婚姻状况联合起来对收入的影响，我们就用到了析因方差分析，如下所示：

import numpy as np
import pandas as pd
from scipy import stats
import statsmodels.stats.anova as anova
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt

def startup():
    psid = pd.read_csv('../datas/PSID.csv')
    model = ols('earnings ~ C(educatn)*C(married)', data=psid.dropna()).fit()
    rst = anova.anova_lm(model)
    print(rst)
    
if '__main__' == __name__:
    startup()

codes/c16c003.py

这里与多因素方差分析的唯一区别就是第10行，将因子变量由相加变为相乘，运行结果为：

images/c16f005.png

上图中最后一列是p值，我们可以看出，教育程度和婚姻状况单独的p值都远小于0.05，所以其对收入的影响是非常显著的。而教育程度与婚姻状况联合起来，p值为0.6999要大于0.05，所以其对收入不会产生显著的影响。