DDA算法和Bresenham算法
DDA算法和Bresenham算法
本文结构如下:
- 1、DDA算法
- 2、Bresenham算法
- 3、代码实现核心部分
1、DDA算法
DDA算法是计算机图形学中最简单的绘制直线算法。其主要思想是由直线公式y = kx + b推导出来的。
我们已知直线段两个端点P0(x0,y0)和P1(x1,y1),就能求出 k 和 b 。
在k,b均求出的条件下,只要知道一个x值,我们就能计算出一个y值。如果x的步进为1(x每次加1,即x = x +1),那么y的步进就为k+b;同样知道一个y值也能计算出x值,此时y的步进为1,x的步进为(1-b)/k。根据计算出的x值和y值,向下取整,得到坐标(x’,y’),并在(x’,y’)处绘制直线段上的一点。
为进一步简化计算,通常可令b取0,将起点看作(0,0)。设当前点为(xi, yi)则用DDA算法求解(xi+1,yi+1)的计算公式可以概括为:
- xi+1 = xi + xStep (1)
- yi+1 = yi + yStep (2)
我们一般通过计算 Δx 和 Δy 来确定xStep和yStep:
- 如果 Δx > Δy ,说明x轴的最大差值大于y轴的最大差值,x轴方向为步进的主方向,xStep = 1,yStep = k;
- 如果 Δy> Δx,说明y轴的最大差值大于x轴的最大差值,y轴方向为步进的主方向,yStep = 1,xStep = 1 / k。
根据这个公式,就能通过(xi,yi)迭代计算出(xi+1、yi+1),然后在坐标系中绘制计算出的(x,y)坐标点。
2、Bresenham算法
Bresenham算法也是一种计算机图形学中常见的绘制直线的算法,其本质思想也是步进的思想,但由于避免了浮点运算,相当于DDA算法的一种改进算法。
设直线的斜率为k,当|k| <=1时,x方向为主步进方向;当|k| >1时,y方向为主步进方向。现以|k| <1时为例,推导Bresenham算法的原理。
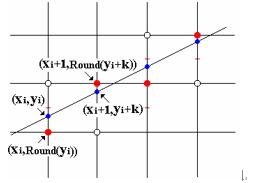
Bresenham算法直线绘制示意图
图片来自:http://st251256589.blog.163.com/blog/static/16487644920114112817666/
图中绘制了一条直线,蓝色点表示该直线上的点,红色点表示光栅下绘制的点。
假设当前点是(xi,yi)
- 如果int(yi+0.5) = yi,则在点(xi, round(yi))处绘制.
- 如果int(yi+0.5) = yi + 1,则在点(xi, round(yi)+1)处绘制。
上述逻辑可简述为:当x方向是主要步进方向时,以每一小格的中点为界,如果当前的yi在中点(图中红色短线)下方,则y取round(yi); 如果当前的yi在中点上方,则y取rund(yi)+1。
引用部分:现考虑这种方法的误差,因为直线的起始点在像素中心,所以误差项d的初值d0=0。x下标每增加1,d的值相应递增。直线的斜率值k,即d=d+k。一旦d≥1,就把它减去1,这样保证d在0、1之间。当d≥0.5时,最接近于当前像素的右上方像素(x+1,y+1)而当d<0.5时,更接近于右方像素(x+1,y)为方便计算,令e=d-0.5,e的初值为-0.5,增量为k。当e≥0时,取当前像素(xi,yi)的右上方像素(x+1,y+1),而当e<0时,更接近于右方像素(x+1,y)可以改用整数以避免除法。由于算法中只用到误差项的符号,因此可作如下替换:
e1 = 2e * Δx。参考:
http://blog.csdn.net/xdg_blog/article/details/52848891
http://www.cnblogs.com/weiweishuo/archive/2013/03/11/2954443.html
3、代码实现
1、DDA算法
void CGView::DrawDDALine(int startx,int starty, int endx, int endy)
{
CDC* pDC = GetDC();
DrawStandLine(pDC);//绘制标准直线
int x0 = startx;
int y0 = starty ;
int x1 = endx;
int y1 = endy;
int color=RGB(255,0,0);
int x;
float dx,dy,y,k;
dx = x1-x0, dy = y1-y0;
k = dy / dx,y = y0;
int x2 = startx;
int y2 = endx;
for(x = x0;x <= x1;x++)
{ //(20,360)是坐标轴的起点
x2 = 20 + x * 30; //30是坐标轴的单位刻度
pDC->Ellipse( x2 - 5, y2 - 5, x2 + 5, y2 + 5 );
y = k * x + k;
y = (int)(y+0.5);
y2 = 360 - y * 30;
}
}
2、Bresenham算法
void CGView::DrawBresenham(int startx,int starty, int endx, int endy)
{
CDC* pDC = GetDC();
DrawStandLine(pDC);//绘制标准直线
int x0, y0, x1, y1;
x0 = startx;
y0 =starty;
x1 = endx;
y1 = endy;
int x, y, dx, dy;
dx = x1-x0, dy = y1- y0;
x = x0;
y = y0;
double k = dy / dx;
//如果 >1,则y方向是主要步进方向,需要转换坐标系方向
if(abs(k)>1){
Swap(startx,starty,endx,endy);
}
int e = -dx; int x2 = 20, y2 = 360; //(20,360)是坐标轴的起点
for (int x=x0; x<=x1; x++)
{
pDC->Ellipse( x2 - 5, y2 - 5, x2 + 5, y2 + 5 );
x2 += 30;
e += 2 * dy;
if (e > 0)
{
y++;
y2 -= 30; //30是坐标轴的单位刻度
e -= 2*dx;
}
}
}
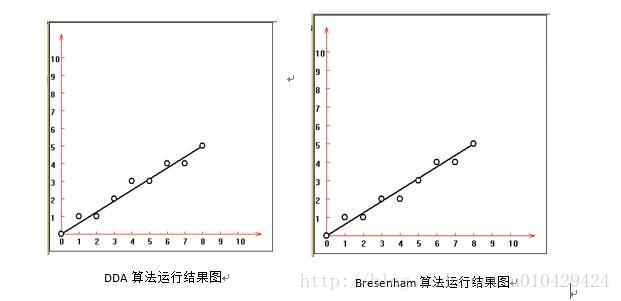
两种算法的运行结果情况如下图所示,从图中可已看出,两种算法都能绘制出直线段,但是在细节稍有不同,当x=4时,DDA算法的y值为3,而Bresenham的算法y为2。在不过从效率上看,由于Bresenham避免了浮点运算,所以效率更高。
本文参考了网上的资料,包括图片、文字等。在文中均给出了链接。时间太久了,代码已经找不到出处了。如有疏漏,请指出。