洛谷 P3373 【模板】线段树 2

Description:

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

Input:

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_）

Output:

输出包含若干行整数，即为所有操作3的结果。

Sample Input:

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

Sample Output:

17
2

Hint:

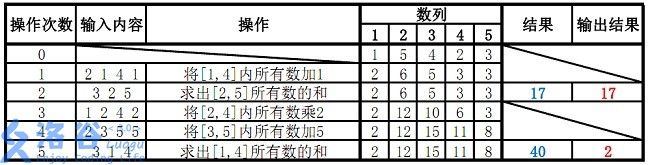
样例说明：

题目链接

题目显然是用线段树来做，具体难点为如何同时实现加法与乘法

加点和乘法可以分别用一个 $lazy$ 惰性标记进行传递

这里传递时有优先级问题，若一个节点同时有加标记和乘标记应该是乘法优先

例如一节点值为 $a$ ，其需要 $+b$ 、 $\times c$ ，应该首先把 $a、b$ 乘上 $c$ 得到 $ac$ 和 $+bc$ ，之后再进行 $+$ 操作得到 $ac+bc$

AC代码:

#include 
using namespace std;

int mod;

class seg_tree {
public:
  typedef long long type_t;
  struct node {
    type_t v, add, mul;
    node(type_t _v = 0, type_t _add = 0, type_t _mul = 1): v(_v), add(_add), mul(_mul) {}
  };

  int n;
  vector<node> tree;

  node Unite(const node &k1, const node &k2) {
    node ans;
    ans.v = k1.v + k2.v;
    return ans;
  }

  void Pull(int o) {
    tree[o] = Unite(tree[o << 1], tree[o << 1 | 1]);
  }

  void Push(int o, int l, int r) {
    int m = (l + r) >> 1;
    if (tree[o].mul != 1) {
      tree[o << 1].add = (tree[o << 1].add * tree[o].mul) % mod;
      tree[o << 1 | 1].add = (tree[o << 1 | 1].add * tree[o].mul) % mod;
      tree[o << 1].mul = (tree[o << 1].mul * tree[o].mul) % mod;
      tree[o << 1 | 1].mul = (tree[o << 1 | 1].mul * tree[o].mul) % mod;
      tree[o << 1].v = (tree[o << 1].v * tree[o].mul) % mod;
      tree[o << 1 | 1].v = (tree[o << 1 | 1].v * tree[o].mul) % mod;
      tree[o].mul = 1;
    }
    if (tree[o].add != 0) {
      tree[o << 1].v += (m - l + 1) * tree[o].add;
      tree[o << 1 | 1].v += (r - m) * tree[o].add;
      tree[o << 1].add += tree[o].add;
      tree[o << 1 | 1].add += tree[o].add;
      tree[o].add = 0;
    }
  }

  void Build(int o, int l, int r, const vector<type_t> &v) {
    if (l == r) {
      tree[o].v = v[l - 1];
      return;
    }
    int m = (l + r) >> 1;
    Build(o << 1, l, m, v);
    Build(o << 1 | 1, m + 1, r, v);
    Pull(o);
  }

  seg_tree(const vector<type_t> &v) {
    n = v.size();
    tree.resize(n << 2);
    Build(1, 1, n, v);
  }
  
  void ModifyAdd(int o, int l, int r, int ll, int rr, type_t v) {
    if (ll <= l && rr >= r) {
      tree[o].v += (r - l + 1) * v;
      tree[o].add += v;
      return;
    }
    Push(o, l, r);
    int m = (l + r) >> 1;
    if (ll <= m) ModifyAdd(o << 1, l, m, ll, rr, v);
    if (rr > m) ModifyAdd(o << 1 | 1, m + 1, r, ll, rr, v);
    Pull(o);
  }
  void ModifyAdd(int ll, int rr, type_t v) {
    ModifyAdd(1, 1, n, ll, rr, v);
  }

  void ModifyMul(int o, int l, int r, int ll, int rr, type_t v) {
    if (ll <= l && rr >= r) {
      tree[o].v = (tree[o].v * v) % mod;
      tree[o].add = (tree[o].add * v) % mod;
      tree[o].mul = (tree[o].mul * v) % mod;
      return;
    }
    Push(o, l, r);
    int m = (l + r) >> 1;
    if (ll <= m) ModifyMul(o << 1, l, m, ll, rr, v);
    if (rr > m) ModifyMul(o << 1 | 1, m + 1, r, ll, rr, v);
    Pull(o);
  }
  void ModifyMul(int ll, int rr, type_t v) {
    ModifyMul(1, 1, n, ll, rr, v);
  }

  node Query(int o, int l, int r, int ll, int rr) {
    if (ll <= l && rr >= r) return tree[o];
    Push(o, l, r);
    int m = (l + r) >> 1;
    node ans;
    if (ll <= m) ans = Unite(ans, Query(o << 1, l, m, ll, rr));
    if (rr > m) ans = Unite(ans, Query(o << 1 | 1, m + 1, r, ll, rr));
    return ans;
  }
  node Query(int ll, int rr) {
    return Query(1, 1, n, ll, rr);
  }
};

int main() {
  ios::sync_with_stdio(false); cin.tie(0);
  int n, m; cin >> n >> m >> mod;
  vector<long long> arr(n);
  for (auto &it : arr) cin >> it;
  seg_tree sgt(arr);
  sgt.Build(1, 1, n, arr);
  for (int i = 0, op, x, y, k; i < m; ++i) {
    cin >> op;
    if (op == 1) {
      cin >> x >> y >> k;
      sgt.ModifyMul(x, y, k);
    }
    else if (op == 2) {
      cin >> x >> y >> k;
      sgt.ModifyAdd(x, y, k);
    }
    else {
      cin >> x >> y;
      cout << sgt.Query(x, y).v % mod << endl;
    }
  }
  return 0;
}