day 1

1.树状数组。。。
查询修改，区间查询修改
应用 求逆序对 cv
二维树状数组


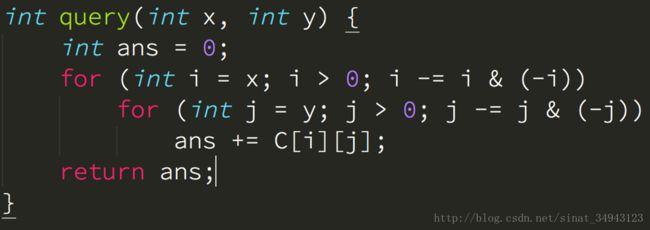
2.线段树
现在我们已经掌握了构造，点修改，点查询，区间修改，区间查询五个最基本的操作
线段树的两个最重要的过程：pushdown和update
线段树的一个隐藏的重要过程——change和pushdown时都要进行的修改
所有的修改函数，最后都要update
所有的函数，开始都要pushdown

盒子和光线 升级版的盒子 矩形 区间最大连续子段和（扫描线） //网盘
3.主席数
我们先假设所有序列中出现的数字已经离散化。主席树中的每个节点存储的是在该区间内出现的数字的个数。这样我们就可以利用类似二分查找的方式确定某个数字的排名，以及特定排名所对应的数字
在实际操作中，序列上的每个位置都对应着一棵主席树。
通过观察可以发现，序列上某一位置的主席树仅仅是在前一个位置的主席树的基础上添加了一个数字（相当于线段树的单点修改）。而线段树单点修改只会修改logn个节点。而其他的节点我们直接延用上一个主席树的节点即可。

区间求k大

#include 
#include 
#include 
#include 
#include 
using namespace std;

#define MAXNODE 2000100
#define MAXM 5100
#define MAXN 100100

int l[MAXNODE], r[MAXNODE], size[MAXNODE], root[MAXN]; //LineTreeint val[MAXN],sortval[MAXN];int n,m,tot;

void Init()
{
    memset(l, 0, sizeof(l));
    memset(r, 0, sizeof(r));
    memset(size, 0, sizeof(size));
    memset(root, 0, sizeof(root));
    tot = 0;
}

void Update(int now)
{
    size[now] = size[l[now]] + size[r[now]];
}

void NewNode(int &now, int pre, int left, int right, int value)
{
    now = ++tot;

    if (left == right) {
        size[now] = size[pre] + 1;
        return;
    }

    int mid = (left + right) >> 1;

    if (value <= sortval[mid]) {
        NewNode(l[now], l[pre], left, mid, value);
        r[now] = r[pre];
    } else {
        NewNode(r[now], r[pre], mid + 1, right, value);
        l[now] = l[pre];
    }

    Update(now);
}

int Find(int now, int pre, int left, int right, int k)
{
    if (left == right)
        return sortval[left];

    int mid = (left + right) >> 1;
    int temp = size[l[now]] - size[l[pre]];

    if (k <= temp)
        return Find(l[now], l[pre], left, mid, k);
    else
        return Find(r[now], r[pre], mid + 1, right, k - temp重要);
}

int main()
{
    //freopen("input.txt","r",stdin);
    while (scanf("%d%d", &n, &m) != EOF) {
        Init();

        for (int i = 1; i <= n; i++)
            scanf("%d", &val[i]);

        memmove(sortval, val, sizeof(int) * (n + 1));
        sort(sortval + 1, sortval + 1 + n);

        for (int i = 1; i <= n; i++)
            NewNode(root[i], root[i - 1], 1, n, val[i]);

        for (int i = 1; i <= m; i++) 
        {
            int l, r, k;
            scanf("%d%d%d", &l, &r, &k);
            int ans = Find(root[r], root[l - 1], 1, n, k);
            printf("%d\n", ans);
        }
    }
}

带修改的主席树

如果允许序列进行修改操作呢？
假设修改了第x个位置上的数字，如果我们对x位置之后的所有的主席树进行更新，最坏情况下可能要消耗O(nlogn)的时间
如何在快速查询和快速修改之间做一个折中？
数据结构嵌套
树状数组套主席树
用树状数组维护一个主席树序列
注意：每个树状数组节点上的主席树，包含该树状数组节点所包含的所有数字。
修改查询类似树状数组

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

#define MAXN     20100
#define MAXNODE  4001000

#define QUERY    0
#define CHANGE   1

struct Question {
    int order;
    int left, right, value;
    Question(int _order, int _left, int _right, int _value)
        : order(_order), left(_left), right(_right), value(_value)
    {}
};
vector q;
int l[MAXNODE] = {0}, r[MAXNODE] = {0}, size[MAXNODE] = {0}, tree[MAXNODE] = {0};
int use[MAXNODE] = {0}, tot = 0;
int val[MAXN], sortval[MAXN], totn = 0, n, m;

void Init()
{
    q.clear();

    for (int i = 1; i <= n; i++)
        tree[i] = ++tot;
}

void AddQuestion(int order, int left, int right, int value)
{
    Question temp(order, left, right, value);
    q.push_back(temp);
}

void Update(int now)
{
    size[now] = size[l[now]] + size[r[now]];
}

int ChangeNode(int pre, int left, int right, int val, int change)
{
    int now = ++tot;

    if (left == right) {
        size[now] = size[pre] + change;
        return now;
    }

    int mid = (left + right) >> 1;

    if (val <= sortval[mid]) {
        l[now] = ChangeNode(l[pre], left, mid, val, change);
        r[now] = r[pre];
        Update(now);
    } else {
        r[now] = ChangeNode(r[pre], mid + 1, right, val, change);
        l[now] = l[pre];
        Update(now);
    }

    return now;
}

int lowbit(int x)
{
    return x & (-x);
}

void TreeAdd(int pos, int val, int change)
{
    for (int i = pos; i <= n; i += lowbit(i))
        tree[i] = ChangeNode(tree[i], 1, totn, val, change);
}

int TreeSum(int pos)
{
    int ans = 0;

    for (int i = pos; i; i -= lowbit(i))
        ans += size[l[use[i]]];

    return ans;
}

int Query(int posnow, int pospre, int left, int right, int k)
{
    for (int i = pospre; i; i -= lowbit(i)) use[i] = tree[i];

    for (int i = posnow; i; i -= lowbit(i)) use[i] = tree[i];

    while (left < right) {
        int mid = (left + right) >> 1;
        int temp = TreeSum(posnow) - TreeSum(pospre);

        if (k <= temp) {
            for (int i = pospre; i; i -= lowbit(i)) use[i] = l[use[i]];

            for (int i = posnow; i; i -= lowbit(i)) use[i] = l[use[i]];

            right = mid;
        } else {
            for (int i = pospre; i; i -= lowbit(i)) use[i] = r[use[i]];

            for (int i = posnow; i; i -= lowbit(i)) use[i] = r[use[i]];

            left = mid + 1;
            k -= temp;
        }
    }

    return sortval[left];
}

int main()
{
    //freopen("input.txt","r",stdin);
    scanf("%d%d", &n, &m);
    Init();

    for (int i = 1; i <= n; i++) {
        scanf("%d", &val[i]);
        sortval[++totn] = val[i];
        AddQuestion(CHANGE, i, 0, val[i]);
    }

    for (int i = 1; i <= m; i++) {
        char command;
        int x, y, z;
        scanf(" %c", &command);

        if (command == 'Q') {
            scanf("%d%d%d", &x, &y, &z);
            AddQuestion(QUERY, x, y, z);
        } else {
            scanf("%d%d", &x, &y);
            sortval[++totn] = y;
            AddQuestion(CHANGE, x, 0, y);
        }
    }

    sort(sortval + 1, sortval + 1 + totn);
    totn = unique(sortval + 1, sortval + 1 + totn) - (sortval + 1);

    for (int i = 0; i < q.size(); i++) {
        if (q[i].order == CHANGE) {
            if (i >= n)
                TreeAdd(q[i].left, val[q[i].left], -1);

            TreeAdd(q[i].left, q[i].value, 1);
            val[q[i].left] = q[i].value;
        } else {
            int ans = Query(q[i].right, q[i].left - 1, 1, totn, q[i].value);
            printf("%d\n", ans);
        }
    }
}