图(3)--拓扑排序与关键路径

一.拓扑排序：

         1.定义： 拓扑排序可以理解为在有向图无环图AOV-网(Activity On Vertex ：用图的顶点表示活动，用弧表示活动之间的优先级)中排成一个具有前后次序的线性序列。

         2.实现方式:

                     1). 输入AOV网络。令 n 为顶点个数。
                     2). 在AOV网络中选一个没有直接前驱的顶点, 并输出之; 
                     3). 从图中删去该顶点, 同时删去所有它发出的有向边;
                     4). 重复以上 2、3 步, 直到：
                              全部顶点均已输出，拓扑有序序列形成，拓扑排序完成

                              或者，图中还有未输出的顶点，但已跳出处理循环。这说明图中还剩下一些顶点，它们都有直接前驱，再也找不到没有前驱的顶点了。这时AOV网络中必定存                                 在有向环。

         3.算法实现：                      

Status Topological Sort(ALGraph G)
{
	       //采用邻接表存储结构。若G无回路，则输出拓扑序列并返回OK，否则ERROR
	        FindInDegree(G，indegree)； //对各顶点求入度indegree[0..vernum-1]
		InitStack(S)；  //建零入度顶点栈
		for(i=0；inextarc)
		     {          
			   k=p—>adivex；//对i号顶点的每个邻接点入度减1           
			   if(！(--indegree[k]))  Push(S，k);   //若入度减为0，则入栈    
	              }//for   
		}//while   
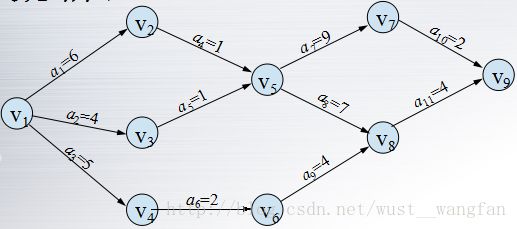
		if(count

二.关键路径（操作带权的有向AOE-网(Activity on Adge:用边表示活动，边上的权值表示活动持续的时间，顶点表示事件，事件表示在它之前的活动全都完成了)）:

              1.关键路径：完成工程最短的时间是从开始点（原点）到结束点（汇点）的最长路径长度，路径最长的路径叫做关键路径。

                        

               从v1到v9的最长路径是(v1,v2,v5,v8,v9)，路径长度是18,故(v1,v2,v5,v8,v9)是一条关键路径

               2.关键活动:l(i)=e(i),即最早开始时间和最晚开始时间相等的活动，关键路径上的所有活动都是关键活动，因此提前完成非关键活动并不能提高工程的进度

                        例如:a6的最早开始时间e(a6)=5,最晚开始时间为l(a6)=8,意味着a6推迟3天完成也不会影响工程的进度，所以分析哪些是关键活动将有利于缩短整个工期。

                        推理怎样求关键活动,即找l(i)=e(i)的活动：

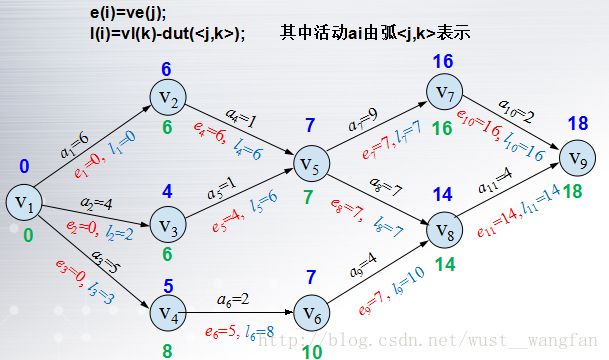
                               设活动ai由弧表示，其持续时间为dut(),故有：

                                      e(i)=ve(j)             (ve(j)表示顶点事件j的最早开始时间)

                                       l(i)=vl(k)-dut()    (vl(k)表示顶点事件k的最晚开始时间) 

                         现在就要求ve(j)和vl(j)，分两步进行:

                                      (1)从ve(0)=0向前递推:ve(j)=Max{ve(i)+dut()}      属于T(所有以第j个顶点为头的弧的集合)

                                      (2)从vl(n-1)=ve(n-1) 向后递推:vl(i)=Min{vl(j)-dut()}      属于S(所有以第i个顶点为尾的弧的集合)

                        于是我们可以得到求关键活动的思想如下：

                                   1）输入e条弧（i，j），建立AOE网的存储结构。
                                   2）从源点v0出发，令ve[0]＝0按拓扑有序求其余各顶点的最早发生时ve[i]（1≤i≤ n-1）。如果得到的拓扑有序序列中顶点个数小于网中顶点数n，则说明网中                                      存在环，不能求关键路径，算法终止；否则执行步骤（3）。
                                   3 ）从汇点vn出发，令vl[n-1]= ve[n-1]，按逆拓扑有序求其余各顶点的最迟发生时间vl[i] (n-2 ≥i≥ 2)；
                                   4）根据各顶点的ve和vl值，求每条弧s的最早开始时间e(s)和最迟开始时间l(s)。若某条弧满足条件e(s)=l(s)，则为关键活动。                  

                3.利用上述思想解题：

                              

                   通过已经求得的各个顶点的ve(i)和vl(i)来求活动的e(i)和l()

                       

                       由于关键活动为e(i)=l(i),所以可得a1,a4,a7,a8,a10,a11为关键活动，相应的V1->V2->V5->V7->V9和V1->V2->V5->V8->V9为关键路径

               4.总结求关键路径的方法：

                       第一步(求每个顶点事件的最早开始时间)： ve(源点) = 0 ；
                                                                                                   ve(j) = Max{ ve(i) + dut()}

                        第二步(求每个顶点的最晚开始时间)：        vl(汇点) = ve(汇点);
                                                                                                   vl(i) = Min { vl(j) – dut()}

                         第三步(求每个活动的最早开始时间和最晚开始时间)： e(s)＝ ve(i)
                                                                                                                         l(s)＝ vl(j) - dut()