【烈日炎炎战后端】 数据结构(0.7万字)
数据结构
- 1. B-树和B+树
- 2. 红黑树
- 3. 跳表
- 4. 排序
- 5. 哈希冲突解决方法
- 6. dfs和bfs
1. B-树和B+树
图片来源: link.
| 关键词 | B-树 | B+树 | 备注 |
| 最大分支,最小分支 | 每个结点最多有m个分支(子树),最少⌈m/2⌉(中间结点)个分支或者2个分支(是根节点非叶子结点)。 | 同左 | m阶对应的就是就是最大分支 |
| n个关键字与分支的关系 | 分支等于n+1 | 分支等于n | 无 |
| 关键字个数(B+树关键字个数要多) | 大于等于⌈m/2⌉-1小于等于m-1 | 大于等于⌈m/2⌉小于等于m | B+树关键字个数要多,+体现在的地方。 |
| 叶子结点相同点 | 每个节点中的元素互不相等且按照从小到大排列;所有的叶子结点都位于同一层。 | 同左 | 无 |
| 叶子结点不相同 | 不包含信息 | 叶子结点包含信息,指针指向记录。 | 无 |
| 叶子结点之间的关系 | 无 | B+树上有一个指针指向关键字最小的叶子结点,所有叶子节点之间链接成一个线性链表 | 无 |
| 非叶子结点 | 一个关键字对应一个记录的存储地址 | 只起到索引的作用 | 无 |
| 存储结构 | 相同 | 同左 | 无 |
B+树是B-树的一种变体,而B-树是二叉排序树的一种升级。二排序树是二路查找,而b+树树多路查找,一个m阶的b+树每个节点最多有m个分支,节点最多会有m个关键字,是有序排列的,每个关键字的左分支节点的内关键字都比它的值小,而有分支节点内的关键字都比他大。
回答思路:
- m阶B-树和B+树都满足**:m阶就是结点最大分支m**。
- 但是B+树的“+”体现在哪呢:首先,B+树的每个结点内关键字n个数最大值比B-树多1。
- 根据1,2得知**:n个关键字与分支的关系:B-树分支为n+1,B-树分支为n**。
- 再考虑叶子结点相同点**:每个节点中的元素互不相等且按照从小到大排列;所有的叶子结点都位于同一层**。
- 再考虑叶子结点不同点**:B+树上有一个指针指向关键字最小的叶子结点,所有叶子节点之间链接成一个线性链表**。
- 再考虑叶子结点不同点2**:B+树结点不包含信息;叶子结点包含信息,指针指向记录**。
- 再考虑非叶子结点不同点**:B-树非叶子结点一个关键字对应一个记录的存储地址;B+树非叶子结点只起到索引的作用**。
【题目拓展:B+树比B树的优势】
- 单一节点存储更多的元素,使得查询的IO次数更少;
这也使得B+树相对于二叉查找树和b-树,都更加矮胖,
- 所有查询都要查找到叶子节点,每次查询IO次数相同,查询性能稳定;
任何关键字的查询必须走从根结点到叶子结点,查询路径长度相同
- 所有叶子节点形成有序链表,便于范围查询。
浅析Mysql索引数据结构演变
https://blog.csdn.net/weixin_34019144/article/details/93181425
2. 红黑树
- 什么是二叉排序(BST)树?
二叉树是空树或者满足一下条件:
- 若它的左子树不为空,则左子树上的左节点的关键字的值均小于根节点关键字的值。
- 若它的右子树不为空,则右子树上的左节点的关键字的值均大于根节点关键字的值。
- 左右子树又分别是一颗二叉排序树
-
什么是平衡二叉(AVL)树?
平衡二叉树首先是二叉查找树,由于树越矮查找效率越高,就有了二叉查找树。二叉平衡树中所有平衡因子只能是-1,0,1三个值 -
什么是平衡因子?
一个结点的平衡因子为其左子树的高度减去右子树高度的差。 -
什么是红黑树?
-
漫画讲解
-
link
-
红黑树是一颗二叉搜索树,它相对二叉搜索树增加了一个存储位来标识结点颜色,可以使 Red 或 Black。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,确保没有一条路径会比其他路径长出两倍。
-
红黑树有什么特点?
-
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点(NIL节点)。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
简单来说:
- 根节点和叶子节点是黑色的;
- 从每个叶子到根的所有路径上不能有两个连续的红色节点;
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点;
-
红黑树什么时候调整?
-
什么情况下会破坏红黑树的规则,什么情况下不会破坏规则呢?我们举两个简单的栗子:
在举例子之前,我们做一点小小的补充!
插入之前所有根至外部节点的路径上黑色节点数目都相同,所以如果插入的节点是黑色肯定错误(黑色节点数目不相同),
而相对的插入红节点可能会也可能不会违反“没有连续两个节点是红色”这一条件,所以插入的节点为红色,如果违反条件再调整
-
红黑树如何调整?
-
变色:
为了重新符合红黑树的规则,尝试把红色节点变为黑色,或者把黑色节点变为红色。
-
左旋转:
逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子
右旋转:
顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子
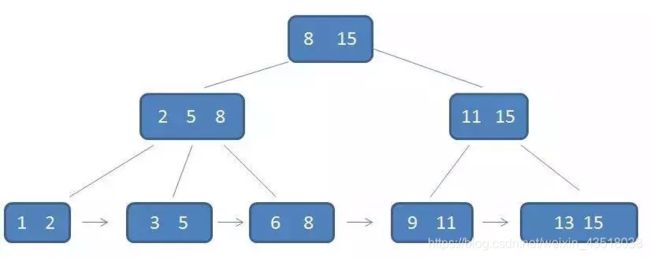
3. 跳表
(https://pics3.baidu.com/feed/8c1001e93901213f14bbb91d6beee6d52e2e9571.png?token=85af3949f546ff1a8bb42ccf9a547492&s=AFC5B25ECEB9588810C1894C03007073)]
-
有序的链表:在一个有序的链表里面,查询跟插入的算法复杂度都是O(n)。
-
跳表:是一种改进的有序的链表,结点是跳过一部分的,从而加快了查询的速度。
图片来源:link
4. 排序
前言:这是我考研时根据率辉老师的《高分笔记》总结的。
| 名称 | 空间复杂度 | 最好情况下时间复杂度 | 最差情况下时间复杂度 | 稳定性 |
|---|---|---|---|---|
| 直接插入排序 | O(1) | 已经有序,双层循环变为单层,O(n) | O(n2 ) | 稳定 |
| 希尔排序 | O(1) | 无 | O(n2) | 不稳定 |
| 冒泡排序 | O(n) | 已经有序,O(n) | O(n2) | 稳定 |
| 快速排序 | O(log2n) | 越无序效率越高,O(log2n) | O(n2) | 不稳定 |
| 简单选择排序 | O(1) | O(n2) | O(n2) | 不稳定 |
| 堆排序 | O(1) | O(log2n) | O(log2n) | 不稳定 |
| 二路归并排序 | O(n) | O(nlog2n) | O(nlog2n) | 稳定 |
| 基数排序 | O(rd) | O(d(n+rd)) | O(d(n+rd)) | 稳定 |
备注:
插入类排序:直接插入排序,希尔排序。
交换类排序:冒泡排序,快速排序。
选择类排序:简单选择排序,堆排序。
记忆方法
1.时间复杂度记忆方法
平均情况下,“快些归队”的时间复杂度为O(nlog2n),其他都为O(n2)。
注: 快:快速排序;些:希尔排序;归:归并排序;队:堆排序;
2.稳定性总结
“情绪不稳定,快些选一堆好友来来聊天吧!”
注: 快:快速排序;些:希尔排序;选:简单选择;堆:堆排序;解决哈希冲突的四种方法
https://www.cnblogs.com/chenchen127/p/11881299.html
5. 哈希冲突解决方法
- 开放地址方法
(1)线性探测:按顺序决定哈希值时,如果某数据的哈希值已经存在,则在原来哈希值的基础上往后加一个单位,直至不发生哈希冲突。
(2)再平方探测:按顺序决定哈希值时,如果某数据的哈希值已经存在,则在原来哈希值的基础上先加1的平方个单位,若仍然存在则减1的平方个单位。随之是2的平方,3的平方等等。直至不发生哈希冲突。
(3)伪随机探测:按顺序决定哈希值时,如果某数据已经存在,通过随机函数随机生成一个数,在原来哈希值的基础上加上随机数,直至不发生哈希冲突。
- 链式地址法(HashMap的哈希冲突解决方法)
对于相同的哈希值,使用链表进行连接。使用数组存储每一个链表。
优点(1)拉链法处理冲突简单,且无堆积现象,即非同义词决不会发生冲突,因此平均查找长度较短;
(2)由于拉链法中各链表上的结点空间是动态申请的,故它更适合于造表前无法确定表长的情况;
(3)开放定址法为减少冲突,要求装填因子α较小,故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1,且结点较大时,拉链法中增加的指针域可忽略不计,因此节省空间;
(4)在用拉链法构造的散列表中,删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。
缺点:指针占用较大空间时,会造成空间浪费,若空间用于增大散列表规模进而提高开放地址法的效率。
- 建立公共溢出区
建立公共溢出区存储所有哈希冲突的数据。
- 再哈希法
对于冲突的哈希值再次进行哈希处理,直至没有哈希冲突。
6. dfs和bfs
https://www.cnblogs.com/wzl19981116/p/9397203.html
1.dfs(深度优先搜索)是两个搜索中先理解并使用的,其实就是暴力把所有的路径都搜索出来,它运用了回溯,保存这次的位置,深入搜索,都搜索完了便回溯回来,搜下一个位置,直到把所有最深位置都搜一遍,要注意的一点是,搜索的时候有记录走过的位置,标记完后可能要改回来;
回溯法是一种搜索法,按条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法;
![]()
例如这张图,从1开始到2,之后到5,5不能再走了,退回2,到6,退回2退回1,到3,一直进行;
理解这种方法比较简单,难的是要怎么用
void dfs(int deep)
{
int x=deep/n,y=deep%n;
if(符合某种要求||已经不能在搜了)
{
做一些操作;
return ;
}
if(符合某种条件且有地方可以继续搜索的)//这里可能会有多种条件,可能要循环什么的
{
a[x][y]='x';//可能要改变条件,这个是瞎写的
dfs(deep+1,sum+1);//搜索下一层
a[x][y]='.';//可能要改回条件,有些可能不用改比如搜地图上有多少块连续的东西
}
}
2.bfs(宽度/广度优先搜索),这个一直理解了思想,不会用,后面才会的,思想,从某点开始,走四面可以走的路,然后在从这些路,在找可以走的路,直到最先找到符合条件的,这个运用需要用到队列(queue),需要稍微掌握这个才能用bfs。
图,bfs就是和它类似,很好的帮助理解,雷从上往下,同时向四面八方的延长(当然不是很严谨的),然后找到那个最近的建筑物,然后劈了它;
![]()
还是这张图,从1开始搜,有2,3,4几个点,存起来,从2开始有5,6,存起来,搜3,有7,8,存起来,搜4,没有了;现在开始搜刚刚存的点,从5开始,没有,然后搜6.。。一直进行,直到找到;
int visit[N][N]//用来记录走过的位置
int dir[4][2]={0,-1,0,1,-1,0,1,0};
struct node
{
int x,y,bits;//一般是点,还有步数,也可以存其他的
};
queuev;
void bfs1(node p)
{
node t,tt;
v.push(p);
while(!v.empty())
{
t=v.front();//取出最前面的
v.pop();//删除
if(找到符合条件的)
{
做记录;
while(!v.empty()) v.pop();//如果后面还需要用,随手清空队列
return;
}
visit[t.x][t.y]=1;//走过的进行标记,以免重复
rep(i,0,4)//做多次查找
{
tt=t;
tt.x+=dir[i][0];tt.y+=dir[i][1];//这里的例子是向上下左右查找的
if(如果这个位置符合条件)
{
tt.bits++;//步数加一
v.push(tt); //把它推入队列,在后面的时候就可以用了
}
}
}
}
3.dfs和bfs的区别
其实有时候两个都可以用,不过需要其他的东西来记录什么的,各自有各自的优势
bfs是用来搜索最短径路的解法是比较合适的
比如求最少步数的解,最少交换次数的解,最快走出迷宫等等,因为bfs搜索过程中遇到的第一个解一定是离最初位置最近的,所以遇到第一个解,一定就是最优解,此时搜索算法可以终止
而如果用dfs,会搜一些其他的位置,需要花相对比较多的时间,需要搜很多次,然后如果找到还不一定是最优解,还要记录这次找的位置,与之后找到的答案进行比较,看看谁才是最优解,这样就比较麻烦
dfs应用比较广泛,用起来比较简单原答案:适合搜索全部的解 。。现在看来比较蠢,其实也没有很适合,只是我当初比较会用dfs而已,来着其实是一样的
如果要搜索全部的解,在记录路径的时候会简单一点,只需要把每一次找的点,放进去答案中就好;并且,相对而言dfs在做很多题目可以用上,比如分治、数位dp,其实就是递归啦,而bfs用的比较少。因为我做的题目比较少,没遇见
原答案:因为要搜索全部的解,在记录路径的时候也会简单一点,而bfs搜索过程中,遇到离根最近的解,并没有什么用,也必须遍历完整棵搜索树。
bfs是浪费空间节省时间,dfs是浪费时间节省空间。
因为dfs要走很多的路径,可能都是没用的,(做有些题目的时候要进行剪枝,就是确定不符合条件的就可以结束,以免浪费时间,否则有些题目会TLE);
而bfs可以走的点要存起来,需要队列,因此需要空间来储存,便是浪费了空间,假设有十层,各个结点有2个子节点,那么储存到第10层就要存 2^10-1 个数据,而dfs只需要存10个数据,但是找到答案的速度相对快一点。
稍微理解之后就可以了,不一定要纠结怎么用,先去做题目,很多都是做着就突然明白怎么用了。