CF888G - Xor-MST（顺带学习Borůvka算法）

今天上课讲到这道题，觉得十分有趣，写了个暴力然后就过挂了，查题解就找到了一个神奇的“B”算法$（Bor\mathring{u}vka）$（这特么是什么啊!）

原题链接1

原题链接2

经过我在baidu上各位大佬的博客上的学习（多谢一位大佬的动态图），我终于明白了这个算法的工作原理。。。

接下来让我这位蒟蒻为各位光临这篇博客的大佬们讲解一下我所理解的这个算法

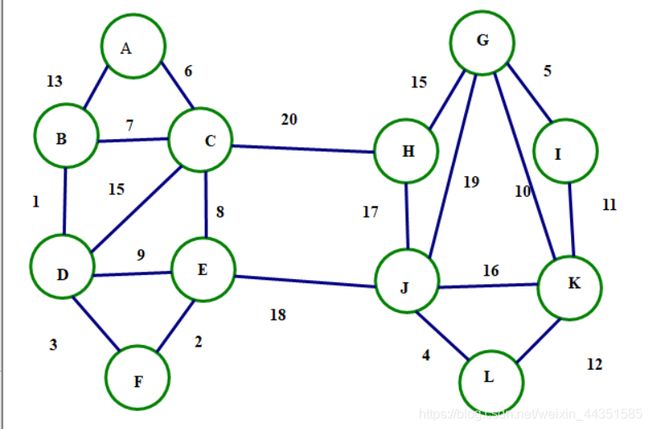
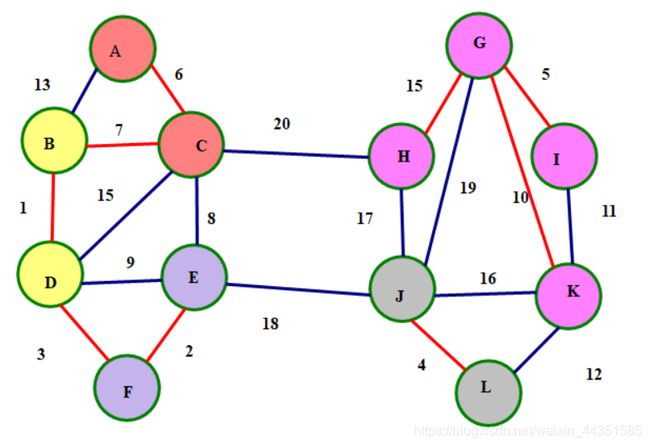
对于一个图

首先我们认为这整个图上的所有点都是一个独立的联通块。

接下来呢

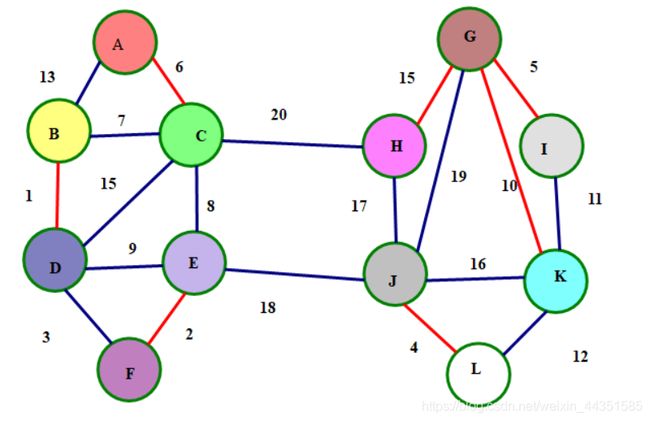
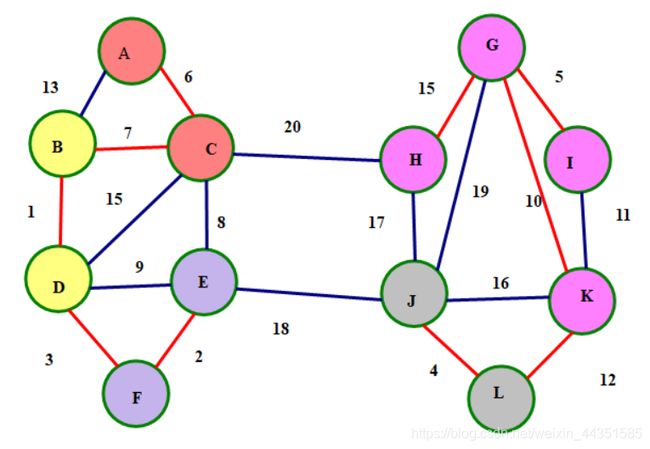
每次让每一个连通块去寻找一条边权最小的边，并与连通块连接

从A号点开始，连6这条边

从B号点开始连1这条边

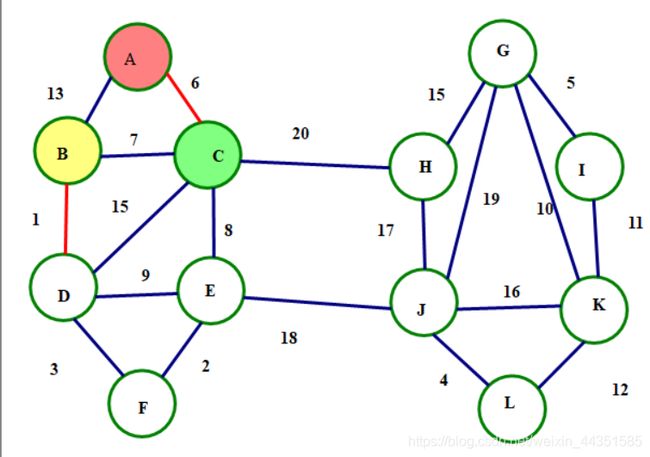
从C号点开始，连6这条边，由于6已和A连，所以无需再连边，AC两点连通

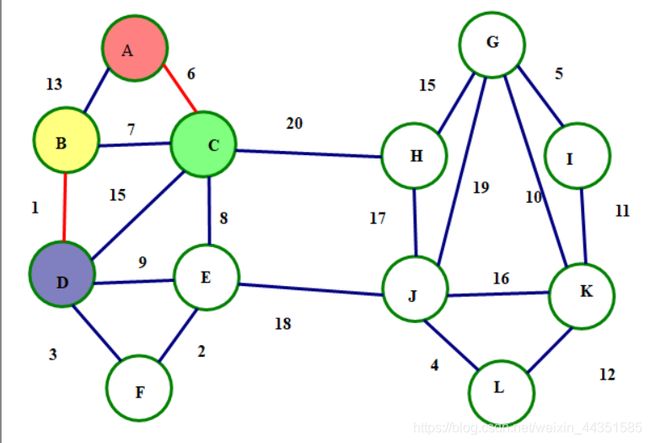
同理BD两点连通

从E号点出发，连2这条边

从F点出发，EF两点连通

从G号点出发，连5这条边。

从H号点出发，连15这条边。

第I号点连5这条边，与G号点相连。

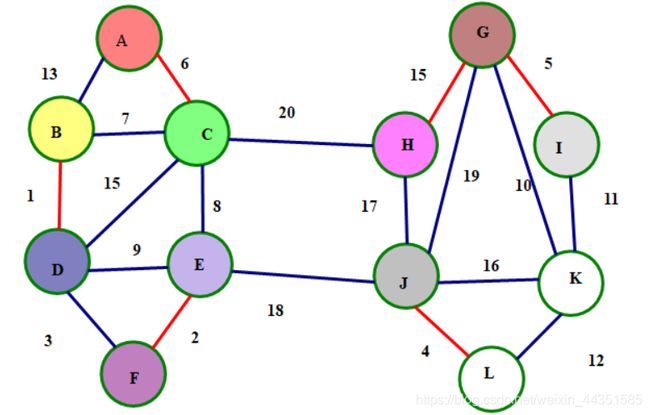
从J号点出发，连4这条边。

从K号点出发，连10这条边。

最后就是从L点出发，JL两点相连。

然后我们就得到了这么几个联通块

再连接两个联通快之间的最短边（BC连边）

DF连边

KL连边

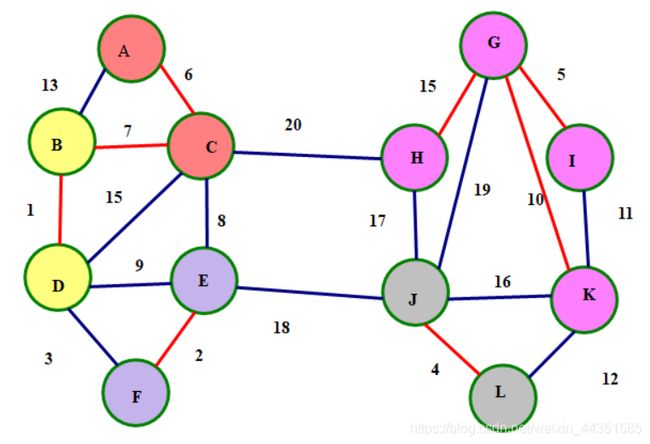
此时整张图就只剩下两个连通块了

再连接他们之间的最短边

然后我们就得到了一个完整的联通图

将点集$A$，$V$分为$S$和$V-S$，一端在$S$内另一端在$V-S$内边权最小的边，一定会在最小生成树中。

复杂度分析：

每次连通块都减少至原来的一半，每一次都要遍历每一条边，所以其复杂度为$O（E\log V）$ $E$为边的个数,$V$为点数

code：

#include
using namespace std;
#define ll long long
const int twx=2e5+100;
const int INF=0x3f3f3f3f;
ll read()
{
    ll sum=0;
    ll flag=1;
    char c=getchar();
    while(c<'0'||c>'9')
    {
        if(c=='-')
        {
            flag=-1;
        }
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        sum=((sum*10)+c-'0');
        c=getchar();
    }
    return sum*flag;
}
struct LV
{
	int x,y,w;
}edge[twx];
int n,m;
int d[twx];// 各子树的最小连外边的权值
int e[twx];// 各子树的最小连外边的索引
bool v[twx];// 防止边重复统计
int fa[twx];
int getfa(int x)
{
	return x==fa[x]?x:(fa[x]=getfa(fa[x]));
}
void add(int x,int y)
{
    fa[getfa(x)]=getfa(y);
}
void init()
{
    n=read();
    m=read();
    for(int i=1;i<=m;i++)
    {
        edge[i].x=read();
        edge[i].y=read();
        edge[i].w=read();
    }
}
int Boruvka()
{
    int tot=0;
    for(int i=1;i<=n;i++)
    {
        fa[i]=i;
    }
    while(1)
    {
        int cur=0;
        for(int i=1;i<=n;i++)
        {
            d[i]=INF;
        }
        for(int i=1;i<=m;i++)  
        {
            int a=getfa(edge[i].x);
            int b=getfa(edge[i].y);
            int c=edge[i].w;
            if(a==b)
            {
                continue ;
            }
            cur++;
            if(c<d[a]||c==d[a]&&i<e[a])
            {
                d[a]=c;
                e[a]=i;
            }
            if(c<d[b]||c==d[b]&&i<e[b])
            {
                d[b]=c;
                e[b]=i;
            }
        }
        if(!cur)
        {
            break ;
        }
        for(int i=1;i<=n;i++)
        {
            if(d[i]!=INF&&!v[e[i]])
            {
                add(edge[e[i]].x,edge[e[i]].y);
                tot+=edge[e[i]].w;
                v[e[i]]=true;
            }
        }
    }
    return tot;
}
void print()
{
    printf("%d",Boruvka());
}
int main()
{
	//freopen(".in","r",stdin);
	//freopen(".out","w",stdout);
    init();
    print();
	return 0;
}

这个模板能拿去AluoguP3366了

上了第一页QAQ

经过实际测试，发现这个算法在一些情况下不如$kruskal$，但是在点少边多的情况下还是能比过$kruskal$的

这题呢就是用了这种思想，每次进行合并。

发现每次合并的集合都是在二进制位下最高位的1的集合，所以从上往下操作，从最高位把集合分开，然后查询两个集合的最小连边。

将所有元素按从小到大排序加入到Trie树，这样的话一个集合内的元素就在一个连续的区间里了

最后就是遍历一遍Trie树统计出答案就行了
code：

#include
using namespace std;
#define ll long long
const int twx=2e5+100;
const int nn=15;
const int INF=0x3f3f3f3f;
ll read()
{
    ll sum=0;
    ll flag=1;
    char c=getchar();
    while(c<'0'||c>'9')
    {
        if(c=='-')
        {
            flag=-1;
        }
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        sum=((sum*10)+c-'0');
        c=getchar();
    }
    return sum*flag;
}
int n;
int a[twx];
int gen;
int L[twx*nn];
int R[twx*nn];
int ch[twx*nn][2];
int tot;
void Insert(int &now,int x,int dd)
{
    if(!now)
    {
        now=++tot;
    }
    L[now]=min(L[now],x);
    R[now]=max(R[now],x);
    if(dd<0)
    {
        return ;
    }
    int asd=a[x]>>dd&1;
    Insert(ch[now][asd],x,dd-1);
}
int add(int now,int val,int dd)
{
    if(dd<0)
    {
        return 0;
    }
    int asd=val>>dd&1;
    if(ch[now][asd])
    {
        return add(ch[now][asd],val,dd-1);
    }
    else
    {
        return add(ch[now][asd^1],val,dd-1)+(1<<dd);
    }
}
ll work(int now,int dd)
{
    if(dd<0)
    {
        return 0;
    }
    if(R[ch[now][0]]&&R[ch[now][1]])
    {
        int asd=INF;
        for(int i=L[ch[now][0]];i<=R[ch[now][0]];i++)
        {
           asd=min(asd,add(ch[now][1],a[i],dd-1)); 
        }
        return work(ch[now][0],dd-1)+work(ch[now][1],dd-1)+asd+(1<<dd);
    }
    if(R[ch[now][0]])
    {
        return work(ch[now][0],dd-1);
    }
    if(R[ch[now][1]])
    {
        return work(ch[now][1],dd-1);
    }
    return 0;
}
void init()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        a[i]=read();
    }
    sort(a+1,a+n+1);
    memset(L,0x3f,sizeof(L));
}
void print()
{
    for(int i=1;i<=n;i++)
    {
        Insert(gen,i,30);
    }
    printf("%lld",work(gen,30));
}
int main()
{
	//freopen(".in","r",stdin);
	//freopen(".out","w",stdout);
    init();
    print();
	return 0;
}

这个是我磨了一天才弄出来的，在交CF的时候有好多稀奇古怪的错误
最后放张截图：

$$普天同庆！$$