微分方程(有阻尼的简谐运动)
微分方程
通过某些变量的变化率来求出原始函数的表达式 变化率比较好表达
例如
-
例如自由落体,物体始终受重力,加速度为 g g g
y ¨ ( t ) = − g y ˙ ( t ) = − g t + v 0 y ( t ) = − ( 1 / 2 ) g t 2 + v 0 t + y 0 \begin{array}{c} \ddot{y}(t)=-g \quad \dot{y}(t)=-g t+v_{0} \\ y(t)=-(1 / 2) g t^{2}+v_{0} t+y_{0} \end{array} y¨(t)=−gy˙(t)=−gt+v0y(t)=−(1/2)gt2+v0t+y0
如已知位移对时间的二阶导数,则可以对两边积分,得到一阶导数和原始函数 -
天体运动,引力大小和方向都在变化,用如下微分方程来描述
F 1 = m 1 a → 1 = G m 1 m 2 ( x → 2 − x → 1 ∥ x → 2 − x → 1 ∥ ) ( 1 ∥ x → 2 − x → 1 ∥ 2 ) {F_{1}=m_{1} \overrightarrow{\mathbf{a}}_{1}}=G m_{1} m_{2}\left(\frac{\overrightarrow{\mathbf{x}}_{2}-\overrightarrow{\mathbf{x}}_{1}}{\left\|\overrightarrow{\mathrm{x}}_{2}-\overrightarrow{\mathbf{x}}_{1}\right\|}\right)\left(\frac{1}{\left\|\overrightarrow{\mathbf{x}}_{2}-\overrightarrow{\mathbf{x}}_{1}\right\|^{2}}\right) F1=m1a1=Gm1m2⎝⎛∥∥∥x2−x1∥∥∥x2−x1⎠⎞⎝⎜⎛∥∥∥x2−x1∥∥∥21⎠⎟⎞
如何求解微分方程
e x a m p l e : example: example:有阻尼的简谐运动
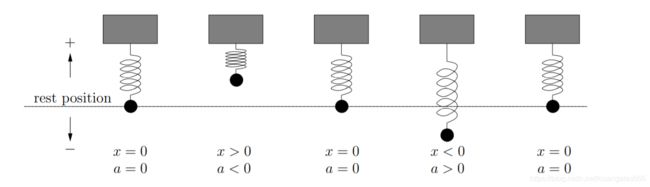
定义弹簧的回复力 f f f
f = − c x f=-c x f=−cx
定义阻力 R R R,阻力大小和速度大小成正比,方向与速度方向相反
R = − μ d x d t R=-\mu \frac{\mathrm{d} x}{\mathrm{d} t} R=−μdtdx
由牛顿第二定律得
m d 2 x d t 2 = − c x − μ d x d t m \frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}=-c x-\mu \frac{\mathrm{d} x}{\mathrm{d} t} mdt2d2x=−cx−μdtdx
为了将二阶导数前的系数归一化,令
2 n = μ m , k 2 = c m 2 n=\frac{\mu}{m}, k^{2}=\frac{c}{m} 2n=mμ,k2=mc
化简得
d 2 x d t 2 + 2 n d x d t + k 2 x = 0 \frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}+2 n \frac{\mathrm{d} x}{\mathrm{d} t}+k^{2} x=0 dt2d2x+2ndtdx+k2x=0
这就是在有阻尼的情况下,物体自由振动的微分方程
l e m m a 1 : lemma1: lemma1:
y ′ ′ + p y ′ + q y = 0 y^{\prime \prime}+p y^{\prime}+q y=0 y′′+py′+qy=0
如果函数 y 1 ( x ) 与 y 2 ( x ) y_{1}(x) 与 y_{2}(x) y1(x)与y2(x)是方程的两个解,那么 y = C 1 y 1 ( x ) + C 2 y 2 ( x ) y=C_{1}y_{1}(x)+C_{2}y_{2}(x) y=C1y1(x)+C2y2(x)也是方程的解,其中 C 1 , C 2 C_{1}, C_{2} C1,C2是任意常数.
p r o o f : proof: proof:
暴力带入
[ C 1 y 1 ′ ′ + C 2 y 2 ′ ′ ] + P ( x ) [ C 1 y 1 ′ + C 2 y 2 ′ ] + Q ( x ) [ C 1 y 1 + C 2 y 2 ] = C 1 [ y 1 ′ ′ + P ( x ) y 1 ′ + Q ( x ) y 1 ] + C 2 [ y 2 ′ ′ + P ( x ) y 2 ′ + Q ( x ) y 2 ] ≡ 0 \begin{aligned} &\left[C_{1} y_{1}^{\prime \prime}+C_{2} y_{2}^{\prime \prime}\right]+P(x)\left[C_{1} y_{1}^{\prime}+C_{2} y_{2}^{\prime}\right]+Q(x)\left[C_{1} y_{1}+C_{2} y_{2}\right] \\ =& C_{1}\left[y_{1}^{\prime \prime}+P(x) y_{1}^{\prime}+Q(x) y_{1}\right]+C_{2}\left[y_{2}^{\prime \prime}+P(x) y_{2}^{\prime}+Q(x) y_{2}\right]\equiv 0 \end{aligned} =[C1y1′′+C2y2′′]+P(x)[C1y1′+C2y2′]+Q(x)[C1y1+C2y2]C1[y1′′+P(x)y1′+Q(x)y1]+C2[y2′′+P(x)y2′+Q(x)y2]≡0
l e m m a 2 : lemma2: lemma2:
对二阶常系数齐次线性微分方程
y ′ ′ + p y ′ + q y = 0 y^{\prime \prime}+p y^{\prime}+q y=0 y′′+py′+qy=0
其特征方程为
r 2 + p r + q = 0 r^{2}+p r+q=0 r2+pr+q=0
当
p 2 − 4 q < 0 p^{2}-4 q<0 p2−4q<0
其两解为
r 1 = α + β i , r 2 = α − β i α = − p 2 , β = 4 q − p 2 2 \begin{array}{c} r_{1}=\alpha+\beta i, \quad r_{2}=\alpha-\beta i \\ \alpha=-\frac{p}{2}, \quad \beta=\frac{\sqrt{4 q-p^{2}}}{2} \end{array} r1=α+βi,r2=α−βiα=−2p,β=24q−p2
故微分方程两解为
y 1 = e ( α + β i ) x , y 2 = e ( α − β i ) x y_{1}=\mathrm{e}^{(\alpha+\beta i) x}, y_{2}=\mathrm{e}^{(\alpha-\beta i) x} y1=e(α+βi)x,y2=e(α−βi)x
利用欧拉公式
e i θ = cos θ + i sin θ \mathrm{e}^{\mathrm{i} \theta}=\cos \theta+\mathrm{i} \sin \theta eiθ=cosθ+isinθ
得
y 1 = e ( α + β i ) x = e α x ⋅ e β x i = e α x ( cos β x + i sin β x ) y 2 = e ( α − β i ) x = e α x ⋅ e − β x i = e α x ( cos β x − i sin β x ) \begin{array}{l} y_{1}=\mathrm{e}^{(\alpha+\beta i) x}=\mathrm{e}^{\alpha x} \cdot \mathrm{e}^{\beta x i}=e^{\alpha x}(\cos \beta x+i \sin \beta x) \\ y_{2}=\mathrm{e}^{(\alpha-\beta i) x}=\mathrm{e}^{\alpha x} \cdot \mathrm{e}^{-\beta x i}=\mathrm{e}^{\alpha x}(\cos \beta x-\mathrm{i} \sin \beta x) \end{array} y1=e(α+βi)x=eαx⋅eβxi=eαx(cosβx+isinβx)y2=e(α−βi)x=eαx⋅e−βxi=eαx(cosβx−isinβx)
由 l e m m a 1 lemma1 lemma1
y ˉ 1 = 1 2 ( y 1 + y 2 ) = e α x cos β x y ˉ 2 = 1 2 i ( y 1 − y 2 ) = e α x sin β x \begin{array}{l} \bar{y}_{1}=\frac{1}{2}\left(y_{1}+y_{2}\right)=\mathrm{e}^{\alpha x} \cos \beta x \\ \bar{y}_{2}=\frac{1}{2 \mathrm{i}}\left(y_{1}-y_{2}\right)=\mathrm{e}^{\alpha x} \sin \beta x \end{array} yˉ1=21(y1+y2)=eαxcosβxyˉ2=2i1(y1−y2)=eαxsinβx
y ˉ 1 , y ˉ 2 \bar{y}_{1},\bar{y}_{2} yˉ1,yˉ2都是方程的解
y ˉ 1 y ˉ 2 = e α x cos β x e α x sin β x = cot β x \frac{\bar{y}_{1}}{\bar{y}_{2}}=\frac{e^{\alpha x} \cos \beta x}{e^{\alpha x} \sin \beta x}=\cot \beta x yˉ2yˉ1=eαxsinβxeαxcosβx=cotβx
表明两解线性无关
故方程的通解为
y = e α x ( C 1 cos β x + C 2 sin β x ) y=\mathrm{e}^{\alpha x}\left(C_{1} \cos \beta x+C_{2} \sin \beta x\right) y=eαx(C1cosβx+C2sinβx)
s t a r t : start: start:
d 2 x d t 2 + 2 n d x d t + k 2 x = 0 \frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}+2 n \frac{\mathrm{d} x}{\mathrm{d} t}+k^{2} x=0 dt2d2x+2ndtdx+k2x=0
初值条件
x ∣ t = 0 = x 0 , d x d t ∣ t = 0 = v 0 \left.x\right|_{t=0}=x_{0},\left.\frac{\mathrm{d} x}{\mathrm{d} t}\right|_{t=0}=v_{0} x∣t=0=x0,dtdx∣∣∣∣t=0=v0
特征方程
r = − 2 n ± 4 n 2 − 4 k 2 2 = − n ± n 2 − k 2 r=\frac{-2 n \pm \sqrt{4 n^{2}-4 k^{2}}}{2}=-n \pm \sqrt{n^{2}-k^{2}} r=2−2n±4n2−4k2=−n±n2−k2
本文只讨论小阻尼情况 n < k n
由 l e m m a 2 lemma2 lemma2
x = e − n t ( C 1 cos ω t + C 2 sin ω t ) x=\mathrm{e}^{-n t}\left(C_{1} \cos \omega t+C_{2} \sin \omega t\right) x=e−nt(C1cosωt+C2sinωt)
带入初值条件
x = e − n t ( x 0 cos ω t + v 0 + n x 0 ω sin ω t ) x=\mathrm{e}^{-n t}\left(x_{0} \cos \omega t+\frac{v_{0}+n x_{0}}{\omega} \sin \omega t\right) x=e−nt(x0cosωt+ωv0+nx0sinωt)
辅助角
ω = k 2 − n 2 , A = x 0 2 + ( v 0 + n x 0 ) 2 ω 2 , tan φ = x 0 ω v 0 + n x 0 \omega=\sqrt{k^{2}-n^{2}}, \quad A=\sqrt{x_{0}^{2}+\frac{\left(v_{0}+n x_{0}\right)^{2}}{\omega^{2}}}, \quad \tan \varphi=\frac{x_{0} \omega}{v_{0}+n x_{0}} ω=k2−n2,A=x02+ω2(v0+nx0)2,tanφ=v0+nx0x0ω
x = A e − n t sin ( ω t + φ ) x=A \mathrm{e}^{-n t} \sin (\omega t+\varphi) x=Ae−ntsin(ωt+φ)
物体的运动是周期为 T = 2 π ω T=\frac{2 \pi}{\omega} T=ω2π 的振动。但与简谐振动不同它的振幅 A e − n t A \mathrm{e}^{-n t} Ae−nt随时间 t t t 的增大而逐渐域小,因此,物体随时间 t t t 的增大而趋于平衡位置