现代数字信号处理第七章——卡尔曼滤波
本章讨论的问题如下:
- 新息过程
- 卡尔曼滤波算法和性能
- 卡尔曼滤波应用
一、新息过程
\quad 线性预测器在最小均方误差意义下的预测误差 e ( n ) e(n) e(n)称为新息过程,新息过程 α ( n ) = d ( n ) − d ^ ( n ) = z ( n ) − w H z n − 1 \alpha(n)=d(n)-\hat{d}(n)=z(n)-w^Hz_{n-1} α(n)=d(n)−d^(n)=z(n)−wHzn−1。
\quad 根据维纳滤波正交原理:估计误差与输入信号向量正交, α ( n ) 与 z ( n ) \alpha(n)与z(n) α(n)与z(n)正交。
\quad α ( n ) \alpha(n) α(n)包含了存在于当前观测样本 z n − 1 z_{n-1} zn−1中的新的新息,故而称作新息。
\quad 根据正交原理,新息过程具有如下统计特性:

最小均方误差估计的新息过程
\quad 输 入 为 z ( n ) , 最 佳 权 向 量 为 w ( n ) , 信 号 x ( n ) 为 期 望 响 应 , 则 对 x ( n ) 的 最 小 均 方 误 差 为 x ^ ( n ∣ Z n ) = w H ( n ) z n = w H L n − 1 α ( n ) = b H ( n ) α ( n ) 输入为z(n),最佳权向量为w(n),信号x(n)为期望响应,则对x(n)的最小均方误差为\hat{x}(n|Z_n)=w^H(n)z_n=w^HL_n^{-1}\alpha(n)=b^H(n)\alpha(n) 输入为z(n),最佳权向量为w(n),信号x(n)为期望响应,则对x(n)的最小均方误差为x^(n∣Zn)=wH(n)zn=wHLn−1α(n)=bH(n)α(n),此时 α ( n ) \alpha(n) α(n)为输入为 α ( n ) \alpha(n) α(n)的权向量。根据新息过程的正交性,可以推出:
b i = p a ( i ) E { ∣ α ( i ) ∣ 2 } , p a ( i ) = E [ α ( i ) x ∗ ( n ) ] x ^ ( n ∣ Z n ) = x ^ ( n ∣ Z n − 1 ) + b ∗ ( n ) α ( n ) b_i=\frac{p_a(i)}{E\{|\alpha(i)|^2\}},p_a(i)=E[\alpha(i)x^*(n)]\\\hat{x}(n|Z_{n})=\hat{x}(n|Z_{n-1})+b^*(n)\alpha(n) bi=E{∣α(i)∣2}pa(i),pa(i)=E[α(i)x∗(n)]x^(n∣Zn)=x^(n∣Zn−1)+b∗(n)α(n)
新息过程 → \rightarrow →向量新息过程
\quad 新息过程向量为 α ( n ) = z ( n ) − ( ^ z ) ( n ∣ Z n − 1 ) \alpha(n)=z(n)-\hat(z)(n|Z_{n-1}) α(n)=z(n)−(^z)(n∣Zn−1)其中向量符号 ( ^ z ) ( n ∣ Z n − 1 ) \hat(z)(n|Z_{n-1}) (^z)(n∣Zn−1)表示输入向量 Z n − 1 = { z ( 1 ) , z ( 2 ) , ⋯ , z ( n − 1 ) } Z_{n-1}=\{z(1),z(2),\cdots,z(n-1)\} Zn−1={z(1),z(2),⋯,z(n−1)}对向量 z ( n ) z(n) z(n)的最小均方误差估计。具有如下性质:
- n时刻的新息过程向量与过去所有输入向量正交: E [ α ( n ) z H ( k ) ] = 0 , k ≤ n − 1 E[\alpha(n)z^H(k)]=0,k\le n-1 E[α(n)zH(k)]=0,k≤n−1
- n时刻的新息过程向量与过去所有新息过程向量正交: E [ α ( n ) α H ( k ) ] = 0 , k ≤ n − 1 E[\alpha(n)\alpha^H(k)]=0,k\le n-1 E[α(n)αH(k)]=0,k≤n−1
- 输入数据向量序列 { z ( 1 ) , z ( 2 ) , ⋯ , z ( n − 1 ) } \{z(1),z(2),\cdots,z(n-1)\} {z(1),z(2),⋯,z(n−1)}和新息过程序列 { α ( 1 ) , α ( 2 ) , ⋯ , α ( n − 1 ) } \{\alpha(1),\alpha(2),\cdots,\alpha(n-1)\} {α(1),α(2),⋯,α(n−1)}一一对应: { z ( 1 ) , z ( 2 ) , ⋯ , z ( n − 1 ) } 相 互 等 价 { α ( 1 ) , α ( 2 ) , ⋯ , α ( n − 1 ) } \{z(1),z(2),\cdots,z(n-1)\}相互等价\{\alpha(1),\alpha(2),\cdots,\alpha(n-1)\} {z(1),z(2),⋯,z(n−1)}相互等价{α(1),α(2),⋯,α(n−1)}
二、系统状态方程和观测方程
\quad 对于时不变系统,一般使用状态方程和输出方程即可描述;而对于时变系统,需要使用系统状态方程和观测方程来描述。
状态方程
x ( n ) = F ( n , n − 1 ) x ( n − 1 ) + Γ ( n , n − 1 ) v 1 ( n − 1 ) x(n)=F(n,n-1)x(n-1)+\Gamma(n,n-1)v_1(n-1) x(n)=F(n,n−1)x(n−1)+Γ(n,n−1)v1(n−1)
- 状态向量: x ( n ) x(n) x(n)
- 状态转移矩阵: F ( n , n − 1 ) F(n,n-1) F(n,n−1)
- 系统状态噪声: v 1 ( n − 1 ) v_1(n-1) v1(n−1)
- 状态噪声输入矩阵: Γ ( n , n − 1 ) \Gamma(n,n-1) Γ(n,n−1)
\quad 系统状态噪声: v 1 ( n − 1 ) v_1(n-1) v1(n−1)通常是零均值白噪声,其相关矩阵满足下图: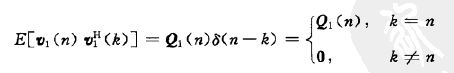
\quad 实际中,通常把 Γ ( n , n − 1 ) v 1 ( n − 1 ) \Gamma(n,n-1)v_1(n-1) Γ(n,n−1)v1(n−1)看作一个整体: x ( n ) = F ( n , n − 1 ) x ( n − 1 ) + v 1 ( n − 1 ) x(n)=F(n,n-1)x(n-1)+v_1(n-1) x(n)=F(n,n−1)x(n−1)+v1(n−1)。
观测方程
z ( n ) = C ( n ) x ( n ) + v 2 ( n ) z(n)=C(n)x(n)+v_2(n) z(n)=C(n)x(n)+v2(n)
三、卡尔曼滤波
已知条件 x ( n ) = F ( n , n − 1 ) x ( n − 1 ) + Γ ( n , n − 1 ) v 1 ( n − 1 ) z ( n ) = C ( n ) x ( n ) + v 2 ( n ) E [ v 1 ( n ) v 1 H ( n ) ] = Q 1 ( n ) E [ v 2 ( n ) v 2 H ( n ) ] = Q 2 ( n ) x(n)=F(n,n-1)x(n-1)+\Gamma(n,n-1)v_1(n-1)\\z(n)=C(n)x(n)+v_2(n)\\E[v_1(n)v_1^H(n)]=Q_1(n)\\E[v_2(n)v_2^H(n)]=Q_2(n) x(n)=F(n,n−1)x(n−1)+Γ(n,n−1)v1(n−1)z(n)=C(n)x(n)+v2(n)E[v1(n)v1H(n)]=Q1(n)E[v2(n)v2H(n)]=Q2(n)
初始条件 x ^ ( 0 ∣ Z 0 ) = E [ x ( 0 ) ] P ( 0 ) = E { [ x ( 0 ) − E [ x ( 0 ) ] ] [ x ( 0 ) − E [ x ( 0 ) ] ] H } \hat{x}(0|Z_0)=E[x(0)]\\P(0)=E\{[x(0)-E[x(0)]][x(0)-E[x(0)]]^H\} x^(0∣Z0)=E[x(0)]P(0)=E{[x(0)−E[x(0)]][x(0)−E[x(0)]]H}
算法流程
- 1.状态一步预测 x ^ ( n ∣ Z n − 1 ) = F ( n , n − 1 ) x ^ ( n − 1 ∣ Z n − 1 ) \hat{x}(n|Z_{n-1})=F(n,n-1)\hat{x}(n-1|Z_{n-1}) x^(n∣Zn−1)=F(n,n−1)x^(n−1∣Zn−1)
- 2.新息过程 α ( n ) = z ( n ) − z ^ ( n ∣ Z n − 1 ) = z ( n ) − C ( n ) x ^ ( n ∣ Z n − 1 ) \alpha(n)=z(n)-\hat{z}(n|Z_{n-1})=z(n)-C(n)\hat{x}(n|Z_{n-1}) α(n)=z(n)−z^(n∣Zn−1)=z(n)−C(n)x^(n∣Zn−1)
- 3.一步预测误差自相关矩阵 P ( n , n − 1 ) = F ( n , n − 1 ) P ( n − 1 ) F H ( n , n − 1 ) + Γ ( n , n − 1 ) Q 1 ( n − 1 ) Γ H ( n , n − 1 ) P(n,n-1)=F(n,n-1)P(n-1)F^H(n,n-1)+\Gamma(n,n-1)Q_1(n-1)\Gamma^H(n,n-1) P(n,n−1)=F(n,n−1)P(n−1)FH(n,n−1)+Γ(n,n−1)Q1(n−1)ΓH(n,n−1)
- 4.新息过程自相关矩阵 A ( n ) = C ( n ) P ( n , n − 1 ) C H ( n ) + Q 2 ( n ) A(n)=C(n)P(n,n-1)C^H(n)+Q_2(n) A(n)=C(n)P(n,n−1)CH(n)+Q2(n)
- 5.卡尔曼增益 K ( n ) = P ( n , n − 1 ) C H ( n ) A − 1 ( n ) K(n)=P(n,n-1)C^H(n)A^{-1}(n) K(n)=P(n,n−1)CH(n)A−1(n)
- 6.状态估计 x ^ ( n ∣ Z n ) = x ^ ( n ∣ Z n − 1 ) + K ( n ) α ( n ) \hat{x}(n|Z_{n})=\hat{x}(n|Z_{n-1})+K(n)\alpha(n) x^(n∣Zn)=x^(n∣Zn−1)+K(n)α(n)
- 7.状态估计误差自相关矩阵 P ( n ) = [ I − K ( n ) C ( n ) ] P ( n , n − 1 ) P(n)=[I-K(n)C(n)]P(n,n-1) P(n)=[I−K(n)C(n)]P(n,n−1)
无偏性
\quad 估计的无偏性值 E [ x ( n ) ] = E [ x ^ ( n ∣ Z n ) ] E[x(n)]=E[\hat{x}(n|Z_{n})] E[x(n)]=E[x^(n∣Zn)],即 E [ ϵ ( n ) ] = E [ x ( n ) − x ^ ( n ∣ Z n ) ] = 0 E[\epsilon(n)]=E[x(n)-\hat{x}(n|Z_{n})]=0 E[ϵ(n)]=E[x(n)−x^(n∣Zn)]=0,在PPT上有卡尔曼滤波满足上述式子的推导,故卡尔曼滤波满足无偏性。
最小均方误差估计特性
\quad 代价函数 J ( n ) = ∑ l = 1 N E [ ∣ e l ( n ) ∣ 2 ] = t r { E [ ϵ ( n ) ϵ H ( n ) ] } J(n)=\sum_{l=1}^NE[|e_l(n)|^2]=tr\{E[\epsilon(n)\epsilon^H(n)]\} J(n)=∑l=1NE[∣el(n)∣2]=tr{E[ϵ(n)ϵH(n)]},当代价函数达到最小值时 K ( n ) = P ( n , n − 1 ) C H ( n ) A − 1 ( n ) K(n)=P(n,n-1)C^H(n)A^{-1}(n) K(n)=P(n,n−1)CH(n)A−1(n),这与卡尔曼滤波算法中增益计算一致,故而卡尔曼滤波满足最小均方误差估计准则。
四、卡尔曼滤波的应用
在维纳滤波中的应用
\quad 在维纳滤波中, R w o = p Rw_o=p Rwo=p。在输入信号和期望信号均平稳时,最优权值为常向量,即状态方程为 w o ( n ) = w o ( n − 1 ) w_o(n)=w_o(n-1) wo(n)=wo(n−1)。由 e o ( n ) = d ( n ) − ( ^ d ) o ( n ) , ( ^ d ) o ( n ) = u T ( n ) w o ∗ ( n ) + e o ( n ) e_o(n)=d(n)-\hat(d)_o(n),\hat(d)_o(n)=u^T(n)w_o^*(n)+e_o(n) eo(n)=d(n)−(^d)o(n),(^d)o(n)=uT(n)wo∗(n)+eo(n)可知,观测方程为 d ∗ ( n ) = u H ( n ) w o ( n ) + e o ∗ ( n ) d^*(n)=u^H(n)w_o(n)+e^*_o(n) d∗(n)=uH(n)wo(n)+eo∗(n)。有状态方程和观测方程就可以用卡尔曼滤波算法求出最优权向量,以实现维纳滤波。
