【开篇】初等数论及其核心内容

【开篇】初等数论及其核心内容

 

一、初等数论的发展历史简介

数学是一门很关注数与形的学科，它们是最基础、最久远的数学概念。克罗内克说过：“上帝创造了自然数，其它都是人的作品”，所以我们选择从数开始说起。数论（Number Theory）专门研究自然数（或整数），这个看似无意义的智力游戏，其实不光是数学家们的思维乐园，它更是孕育新思想、新方法的肥沃土壤。即使我们已经有了耀眼的成就，却好像还不曾见过她的真面目，在其简单的外表下，总有不为人知的深邃。高斯曾经说过：“数学是科学的皇后，而数论则是数学的皇后”，下面就让我们来看看它的一些发展历史。

　　数论最开始的称号就是我们所熟悉的算术，在古希腊时期就有了初步的发展。欧几里得的《几何原本》中就有了一些经典的结论，比如素数有无穷多个，还有大家熟悉的辗转相除法。包括同时期的素数筛选法，对后来的数论研究都很有启发性。古希腊末期的丢潘图唯独偏爱不定方程，所著的《算术》对数进行了超乎想象的讨论。也正是这本书，为今后的数论埋下了神奇的种子。当欧洲文明在中世纪进入漫长的沉寂时，中国数学界却异常地活跃，主要的数学著作中有很多是数论相关的。只是国人不善于将方法转化成理论，仅止于各种方法技巧，并未得到比较深刻的理论体系。

　　文艺复兴时期，数论迎来了它短暂的萌芽。百无聊赖的律师费马，将他的所有业余时间都花在了科学上（主要是数学），而丢潘图的《算术》更是让他深深地陷入了数论的泥潭。仅靠他在书页空白处的笔记，就已经得出了丰富而深刻的结论以及各种奇妙的方法，著名的费马猜想更是足足困扰了后人三百多年。十七、十八世纪是分析学的天下，所有学科都在微积分阴影的笼罩之下。然而全能王欧拉凭借其超人的才华，得到了更多数论方面的深刻结论，并开始挖向了解析数论的宝藏。

                                                    

                                Fermat（1601 - 1665）            Euler（1707 - 1783）          Gauss（1777 - 1855）

　　至此，数论已经有了非常丰富的结论，但缺乏一个完整的理论体系，这也限制了它进一步的发展。高斯的《算术研究》集前人的成就于一体，提出了同余理论并扩展了整数的概念，为代数数论提供了理论储备。尤其是得到了被称为“数论之酵母”的二次互反律，一下子将数论带进了崭新的邻域。《算术研究》标志着数论作为一个学科的建立，并直接将其带入了现代意义的数论。

　　接下来，沿着解析数论和代数数论两个不同的方向，数论在现代数学的道路上飞奔。当与近代最尖端的代数几何相结合时，数论步入了其最深刻的阶段，这就是当今的“算术代数几何”（注意！这是一门学科）。同时，数论还摆脱了以往纯数学的帽子，延伸出了多个应用分支，包括编码学、计算数论、组合数论等，这门古老的学科终于开始服务大众了。

　　也许没有一个学科像数论这样，在理论数学、应用数学甚至娱乐数学中都扮演者重要的角色。令人欣慰的是，只要有小初中学数学的知识，就可以开始这段旅程。但我们必须得承认看似简单的东西，其背后也藏着巨大的秘密。需要人类几代几代人的不断探索，才对它的认识更加的深刻一点点。下面我们就来介绍初等数论学习过程中最为主要的东西，抓住本质，从整体认识到具体细节。不然，我们很有可能在学习的深海中迷失哟，哈哈。

 

二、初等数论内容概述

2.1  数论是什么

如其名，数论研究的是数的理论，更准确的说是研究整数的理论。这门理论的核心问题有两种，分别为

• 解整数方程（组）：如求方程x2 + y2 = z2的整数解；
• 素数分布问题：如素数有多少个？

我们称正整数 n 为素数：如果它只有1和n两个正因子。如 2, 3 都是素数, 4, 6 却不是一因为它们有一个正因子是2, 1也不是素数因为它只有一个正因子。

下面我们就从这两个问题出发，介绍一下初等数论的一些相关内容。

• 解整数方程

小学初中的时候，我们大家肯定都接触过的鸡兔同笼等等类似问题。如假设市场上有人在卖鸡，母鸡五元一只，公鸡二元一只，小鸡五角一只，现在有一个人 用100元钱恰好买了 100只鸡，问他各买了多少只母鸡、公鸡和小鸡 ？通过代数的方法，我们很快就能把问题归结到求解整数方程上面，如下：

列方程：假设母鸡 x只、公鸡 y只、小鸡 z只，那么可以列出方程组：

                                                      

注意，这虽然不是整数方程组，但是把第一行乘以 2 就得到如下的整数方程组：

                                                     

把这个方程组第二个方程减去第一个，得到

                                                        9x + 3y = 100.

实际上，这个方程是不可解的，因为左边可以被3整除，但是100是不被3整除的 ！所以我们应该树立一个意识：
解方程的时候，首先要去判断方程可不可解，然后再去解方程。

接下来，我们通过一些经典的例子来阐释解整数方程问题对于数学的重要性，一些典型的例子是我们掌握各种理论的有力工具！这些例子或多或少都和直角三角形相关。我们都知道一个直角三角形满足勾股定理/商高定理说的是：如果一个直角三角形的两条直角 边长度分别为x和y,斜边的长度为z,那么  ”

                                                               

所以，来看看我们的第一个例子就是求解勾股三角形”

例1.勾股三角形：求出所有的边长为整数的直角三角形，即求方程       的所有的正整数解。

费马看到这，就想如果把上面例 1 的方程中的平方全部换成 k 次方呢？其中 k 是大于等于3的整数呢。一番思考之后，提出了他的猜想一现在被称为费马大定理。

定理 1 (Wiles-Taylor；费马大定理).     对于任何大于等于3的整数k,方程     没有xyz    0的整数解。

而且他在他的书的那一页写上'‘这儿地方太小写不下去这个证明”。这个问题 在1995年最终被Wiles和Taylor解决，历时350多年。下面我们给大家介绍一个千年历史名题一同余数问题。问题在公元900多年在阿拉伯人的一部著作里面明确提出。我们称一个 正整数 n 是同余数，如果它是一个边长均为有理数的直角三角形的面积。如，通过勾股定理，我们知道(3, 4, 5)构成一个勾股三角形，所以6 = 1/2  x 3 x 4是一个同余数。

例2.同余数问题：给定一个正整数n,判断它是不是一个同余数。

这个问题的当前进展比较少，1956年，Heegner证明了如果p是一个形如 8n + 5 的素数，那么 p —定是一个同余数。这个问题的进展比较缓慢。2012年，田野证明了给定正整 数k,在形如8n + 5 的正整数里面有无穷多个同余数。具体最新的进展，各位可以参见近年来的文献。

• 素数分布问题

在正式的介绍素数分布问题之前，大家知道下面这个人是谁吗 ？

                                                                      

他就是大家应该都知道的陈景润。那他证明了什么？是“1 + 2 = 3”？还是“1 + 2”？ 对，陈景润证明“1 + 2”，在这里我要给大家正名“1 + 1” ！为什么要做这件事情呢？因为自从陈景润的事迹被宣传之后，好多人把“1 + 1”和 "1 + 1 = 2”弄混淆了。

要谈"1 + 1”，首先得从命题"a + b”开始谈起。所谓的"a + b”指的是一个充分大的偶数一定能写成一个不超过a个素数乘积与一个不超过b个素数乘积之和。要注意这里自然包括零个素数乘积的 1。从而"1 + 1”指的是一个充分大的偶数一定能写成一个素数与一个素因子个数不超过1的正整数(包括1) 之和这一命题，而不是一个充分大的偶 数一定能写成两个素数之和，更不是"1 + 1 = 2”是一个数学恒等式！

这里的"一个充分大的偶数一定能写成两个素数之和”是我们下面要介绍的偶数哥德巴赫猜想充分大的情形。

 

猜想1.1.1 (偶数哥德巴赫猜想).     任何一个大于等于4的偶数一定是两个素数之和。

例如4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5,10 = 3 + 7 = 5+ 5 等等。对应的还有奇数哥德巴赫猜想/定理：任何一个大于等于7的整数一定是三个素数之和。1937年，前苏联数学家Vinogradov证明了三素数定理，即一个充分大的奇数一定是三个素数之和。2013年，法 国科学院院—Helfgott完全证明了奇数哥德巴赫猜想。而偶数哥德巴赫猜想的最好的结果还是陈景润的。

       

       下面我们回到素数个数问题上来。我们指的素数按照顺序排：2, 3, 5, 7,11,13 •…。那 第一个问题：能不能无限的排下去？即

例3.素数个数问题：素数一共有多少个？

这个问题的答案可以从奇数哥德巴赫定理我们可以推出。假如素数只有有限个，譬如 n个，则大于等于7 的奇数最多只有个，矛盾！从而素数有无穷个。

       既然素数有无穷个，那数学家就想x以内的素数个数n(x)是如何变化的？有没有一个公式很好的表达 ？为了让大家对  有些感受，我们列出30以内的素数：2, 3, 5, 7,11,13,17, 19, 23, 29，所以= 8,   = 10。高斯通过素数表，在十五六岁的时候就猜出 和  差不多，甚至猜出 与  差的就更少，这也就是著名的素数定理。

 

定理2 (素数定理).   用  表示x以内的素数个数，则当  时，

                                                                         

 的逼近有了，那这个逼近究竟能有多好呢 ？ Riemann 提出了如下的猜想。

 

猜想1.1.2 (黎曼猜想).    存在正常数 C,使得对 x > 3 均有  

上面这几个是围绕单个素数的分布情况？那么素数对的分布情况又是怎样的呢？

一 对素数(p, p')称为李生素数如果 。例如 (3, 5)、(5, 7)、(11,13)、(17,19)……

猜想1.1.3 (李生素数猜想). 李生素数有无穷多对。

在孪生素数上面做出重大贡献的有华裔数学家张益达，感兴趣的朋友，可自行查阅文献了解。

 

2.2  初等数论主要内容

初等数论的主要内容集中在解整数方程，当然是用初等的方法来解整数方程。 概况起来有五种方法和两个定理。下面我们对它们做一个简单的介绍。

2.2.1  五种方法

解整数方程的五种方法包括辗转相除法、唯一分解法、有理直线法、模算术/同余和 费马无穷下降。

下面我们对这五种解法逐一介绍。

解整数方程的第一种方法称为辗转相除法：就是把带余除法不停的用，直到余数为零。如下：

                                                                       15 = 2 x 6 + 3,

                                                                       6 = 2 x 3 + 0.

从而可以求出15和6的最大公因子为3。典型的应用是下面的量水问题。

 

例4 （量水问题）.能否只用两个无刻度的容量分别为17毫升和38毫升的水杯和不限量的水量出1毫升水？

          第二种方法是唯一分解法，它主要是用正整数可以唯一的分解为素数方幕的乘积这 个事实。这种方法的典型例子是开不尽方的数是无理数，如下

例5.   不是有理数。

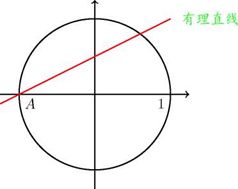
第三种方法我们称之为有理直线法。最经典的例子是求解例1中的勾股三角形。由于 z   0,可以把方程  两边同时除以 z, 得到   ,这就对应到单位圆   的有理点。

                                                           

 

由韦达定理，单位圆的有理点和过（―1, 0）的斜率为有理数的直线（称为有理直线）互相对应。据此可以求得所有勾股三角形。

第四种方法我们称为模算术/同余：模m运算是我们生活中星期（模7）运算、月份、 时钟（模12）运算的推广，两个整数做模m的加减乘的结果丢掉m的倍数，只留下余数。 例子如下

 

例6. 一个数的平方和另一个数平方的两倍之差不可能是3,即： 不可解。

注意，我们以后谈可不可解，只要没有特殊说明，都是指的是在整数范围内的可不可解"

最后一种解法是费马在研究费马大定理 k = 4的情形是发明的，在文献里一般称为费马无穷下降法。

 

例7.   没有  的整数解。

这一解法的基本想法是如果有一组正整数解（x, y, z）,想办法找到一个更小的正整数 解（x',y',z‘）；通过不停的用这一性质、无穷的下降下去，我们得到的解越来越小，但是正整数不可能无限的递降，从而得到矛盾。这也是无穷下降法的名称的由来。

2.2.2 两个定理

初等数论的核心两个定理是中国剩余定理和二次互反律。

第一个核心定理是中国剩余定理。它表明只要m和n互素，则模m的运算和模n的运算互相独立。而它们不互素的时候会有影响的，如一个数四四数剩2却不可能六六数剩1。 因为四四数剩2—定是一个偶数，六六数剩1 一定是一个奇数，故不可能。典型的例子是 《孙子算经》中的/物不知数”

例8 （物不知数）.今有物不知其数，三三数之剩二；五五数之剩三；七七数之剩二。问物几何？

          用现在的语言是说：现有一堆物品，三个三个的数最后剩两个，五个五个的数最后 剩三个，七个七个的数最后剩两个。问这堆物品有多少个？

 

二次互反律是初等数论的又一核心定理。它是对称的观点解方程的体现！这个定理 在说对于给定不同奇素数p,q,方程 和方程  的可解性密切相关。 具体说来如果 p, q 有一个是形为4k+ 1, 则它们可解性一致；否则相反。

至此，上面便是我们初等数论开篇所要讲述的内容。

 

注：此系列专题主要参考书籍是《初等数论》（3rd），潘承洞，2013，

这本书个人觉得可以算初等数论在国内最好的、并且使用最广泛的初等数论教材，注重思想和理论体系的建立。结构清晰合理，表述严格精准。有大量的习题，而且还有不少的延展知识。此外，如有读者需要可扫描左端二维码关注公众号后，说明来意。我可分享它的电子版。仅用于个人学习之用哟。