概率潜在语义分析(PLSA)
文章目录
- 基本概要
- 生成模型和共现模型
- 概率潜在语义分析的算法
基本概要
概率潜在语义分析是一种利用概率生成模型对文本集合进行话题分析的无监督学习方法。
模型最大的特点就是用隐变量表示话题。整个模型表示文本生成话题,话题生成单词,从而得到单词-文本共现数据的过程。假设每个文本由一个话题分布决定,每个话题由一个单词分布决定。
概率潜在语义分析受潜在语义分析的启发,1999年由Hofmann提出。最初用于文本数据挖掘,后来扩展至其他领域。
上面的说法比较抽象,下面采用更加具体的说法。给定一个文本集合(一句句的话),每个文本(一句话)讨论若干个话题,每个话题由若干个单词表示。对文本集合进行概率潜在语义分析,就能发现每个文本的话题,以及每个话题的单词。
这时候就可以发现似乎可以对上面的情况来进行概率统计建模了。首先有话题的概率分布,这个概率分布是无法探知但是确实存在的,就是隐变量;然后有给定话题下文本的条件概率分布;还有给定话题下单词的条件概率分布。概率潜在语义分析就是发现由隐变量表示的话题,就是潜在语义。
下面来建立具体的概率模型。
生成模型和共现模型
假设有单词集合 W = { w 1 , w 2 , ⋯ , w M } W=\left\{w_{1}, w_{2}, \cdots, w_{M}\right\} W={w1,w2,⋯,wM};文本集合 D = { d 1 , d 2 , ⋯ , d N } D=\left\{d_{1}, d_{2}, \cdots, d_{N}\right\} D={d1,d2,⋯,dN};以及话题集合 Z = { z 1 , z 2 , ⋯ , z K } Z=\left\{z_{1}, z_{2}, \cdots, z_{K}\right\} Z={z1,z2,⋯,zK},以及各自对应的随机变量w,d,z。那么生成模型主要通过以下步骤生成文本-单词共现数据。
- 依据先验概率分布 P ( d ) P(d) P(d),从文本集合中随机选取N次文本,对每个文本执行下面的操作;
- 在文本d给定的条件下,依据条件概率分布 P ( z ∣ d ) P(z|d) P(z∣d),从话题集合随机选取一个话题z,共生成L个话题,L是文本长度;
- 在话题z给定的条件下,依据条件概率分布 P ( w ∣ z ) P(w|z) P(w∣z),从单词集合中随机选取一个单词w。
生成模型中,单词变量w与文本变量d是观测变量,话题变量z是隐变量。也就是说模型生成的是(w,z,d)的集合,但观测到的是(w,d)也就是单词-文本的集合。观测到的数据表示为单词-文本矩阵T的形式,矩阵T的行表示单词,列表示文本,元素表示共现次数。
单词-文本对的生成概率为
P ( w , d ) = P ( d ) P ( w ∣ d ) = P ( d ) ∑ z P ( w , z ∣ d ) = P ( d ) ∑ z P ( z ∣ d ) P ( w ∣ z ) \begin{aligned} P(w, d) &=P(d) P(w | d) \\ &=P(d) \sum_{z} P(w, z | d) \\ &=P(d) \sum_{z} P(z | d) P(w | z) \end{aligned} P(w,d)=P(d)P(w∣d)=P(d)z∑P(w,z∣d)=P(d)z∑P(z∣d)P(w∣z)
上式就是生成模型的定义。
上面的模型包含了一个基本假设,也就是第二个等式为什么能到第三个等式,那就是在话题z给定的条件下,单词w与文本d条件独立。也就是说一句话产生了话题,话题和一些有代表性的单词相关,这些单词和一些句子就是该话题下常常共现的,我们用单词-文本矩阵来统计这样的共现情况。
共现模型的表达式和生成模型一样,文本单词的共现矩阵T出现的概率,就是所有单词-文本对(w,d)生成概率的乘积:
P ( T ) = ∏ ( w , d ) P ( w , d ) n ( w , d ) P(T)=\prod_{(w, d)} P(w, d)^{n(w, d)} P(T)=(w,d)∏P(w,d)n(w,d)
其中
P ( w , d ) = ∑ z ∈ Z P ( z ) P ( w ∣ z ) P ( d ∣ z ) P(w, d)=\sum_{z \in Z} P(z) P(w | z) P(d | z) P(w,d)=z∈Z∑P(z)P(w∣z)P(d∣z)
虽然生成模型与共现模型在概率公式意义上是等价的,但是拥有不同的性质。共现模型认为,z生成了w,z生成了d。而生成模型认为d生成了z,z生成了w。就是说共现模型是以z发生为条件,平等地研究w和d的概率,而生成模型是以d发生为条件,研究给定d时的z概率,再研究给定z时的w的概率。虽然两者都是表达 P ( w , d ) P(w,d) P(w,d)。
整个概率潜在语义分析模型中,三个随机变量之间的关系可表示如下:
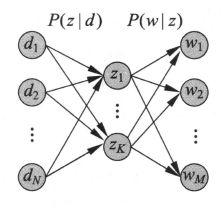
所以这K个隐变量也就是话题的作用就是,对数据进行了更简洁地表示,减少了学习过程中过拟合的可能性。
共现模型的矩阵乘积形式可表示如下
X ′ = U ′ Σ ′ V ′ T X ′ = [ P ( w , d ) ] M × N U ′ = [ P ( w ∣ z ) ] M × K Σ ′ = [ P ( z ) ] K × K V ′ = [ P ( d ∣ z ) ] N × K \begin{aligned} X^{\prime} &=U^{\prime} \Sigma^{\prime} V^{\prime \mathrm{T}} \\ X^{\prime} &=[P(w, d)]_{M \times N} \\ U^{\prime} &=[P(w | z)]_{M \times K} \\ \Sigma^{\prime} &=[P(z)]_{K \times K} \\ V^{\prime} &=[P(d | z)]_{N \times K} \end{aligned} X′X′U′Σ′V′=U′Σ′V′T=[P(w,d)]M×N=[P(w∣z)]M×K=[P(z)]K×K=[P(d∣z)]N×K
它和潜在语义分析模型的区别就是,U,V是非负且规范化的,表示的是条件概率分布,而潜在语义分析模型的U和V是正交的,未必非负,不表示概率分布。
模型的目标是共现概率 P ( w , d ) P(w,d) P(w,d)达到极大,那就说明d和w属于话题z的概率是最高的
概率潜在语义分析的算法
概率潜在语义分析模型是含有隐变量的模型,其学习通常使用EM算法。
推导过程详细可参考《统计学习方法》345-346页,这里说一下书中最后总结的计算流程

其实参数只有两个(严格来说是两组,但在求解时可视为两项),一个是 P ( z k ∣ d j ) P(z_k|d_j) P(zk∣dj),一个是 P ( w i ∣ z k ) P(w_i|z_k) P(wi∣zk)。再加一个概率和为1的约束,拉格朗日求极大,得到参数此时的解,然后回过去求期望得到新表达式,反复迭代即可。