概率潜在语义分析(Probabilistic Latent Semantic Analysis,PLSA)
文章目录
- 1. 概率潜在语义分析模型
- 1.1 基本想法
- 1.2 生成模型
- 1.3 共现模型
- 1.4 模型性质
- 2. 概率潜在语义分析的算法
概率潜在语义分析(probabilistic latent semantic analysis,PLSA),也称概率潜在语义索引(probabilistic latent semantic indexing,PLSI)
- 利用
概率生成模型对文本集合进行话题分析的无监督学习方法 - 最大特点:用隐变量表示话题
- 整个模型表示
文本生成话题,话题生成单词,从而得到单词-文本共现数据的过程 - 假设每个文本由一个话题分布决定,每个话题由一个单词分布决定
1. 概率潜在语义分析模型
概率潜在语义分析 模型有生成模型,以及等价的共现模型
1.1 基本想法
- 给定文本集合,每个文本讨论若干个话题,每个话题由若干个单词表示
- 对文本集合进行
概率潜在语义分析,就能够发现每个文本的话题,以及每个话题的单词 - 话题是不能从数据中直接观察到的,是潜在的
1.2 生成模型
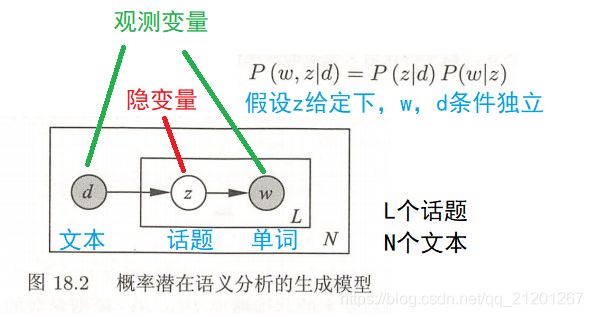
文本-单词共现数据 T T T 的生成概率为 P ( T ) = ∏ ( w , d ) P ( w , d ) n ( w , d ) P(T) = \prod\limits_{(w,d)} P(w,d)^{n(w,d)} P(T)=(w,d)∏P(w,d)n(w,d)
P ( w , d ) = P ( d ) P ( w ∣ d ) = P ( d ) ∑ z P ( w , z ∣ d ) = P ( d ) ∑ z P ( z ∣ d ) P ( w ∣ z ) P(w,d) = P(d)P(w|d) = P(d)\sum\limits_z P(w,z|d) = P(d)\sum\limits_z P(z|d)P(w|z) P(w,d)=P(d)P(w∣d)=P(d)z∑P(w,z∣d)=P(d)z∑P(z∣d)P(w∣z)
1.3 共现模型

文本-单词共现数据 T T T 的生成概率为 P ( T ) = ∏ ( w , d ) P ( w , d ) n ( w , d ) P(T) = \prod\limits_{(w,d)} P(w,d)^{n(w,d)} P(T)=(w,d)∏P(w,d)n(w,d)
P ( w , d ) = ∑ z ∈ Z P ( z ) P ( w ∣ z ) P ( d ∣ z ) P(w,d) = \sum\limits_{z\in Z} P(z)P(w|z)P(d|z) P(w,d)=z∈Z∑P(z)P(w∣z)P(d∣z)
文本数据基于如下的概率模型产生(共现模型):
- 首先有话题 z 的概率分布
- 然后有话题 z 给定条件下 文本 的条件概率分布
- 以及话题 z 给定条件下 单词 的条件概率分布
1.4 模型性质
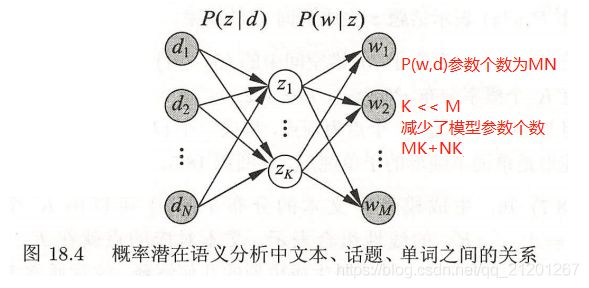
概率潜在语义分析通过话题对数据进行了更简洁地表示,减少了学习过程中过拟合的可能性
2. 概率潜在语义分析的算法
概率潜在语义分析模型是含有隐变量的模型,其学习通常使用 EM算法。
模型参数估计的EM算法:
输入:单词集合 W = { w 1 , w 2 , . . . , w M } W=\{w_1,w_2,...,w_M\} W={w1,w2,...,wM},文本集合 D = { d 1 , d 2 , . . . , d N } D=\{d_1,d_2,...,d_N\} D={d1,d2,...,dN},话题集合 Z = { z 1 , z 2 , . . . , z K } Z=\{z_1,z_2,...,z_K\} Z={z1,z2,...,zK},共现数据 { n ( w i , d j ) } , i = 1 , 2 , . . . , M ; j = 1 , 2 , . . . , N \{n(w_i,d_j)\},i=1,2,...,M; j=1,2,...,N {n(wi,dj)},i=1,2,...,M;j=1,2,...,N
输出: P ( w i ∣ z k ) P(w_i|z_k) P(wi∣zk), P ( z k ∣ d j ) P(z_k|d_j) P(zk∣dj)
- 设置参数 P ( w i ∣ z k ) P(w_i|z_k) P(wi∣zk), P ( z k ∣ d j ) P(z_k|d_j) P(zk∣dj) 的初始值
- 迭代执行以下 E 步, M 步,直到收敛为止
E 步:
P ( z k ∣ w i , d j ) = P ( w i ∣ z k ) P ( z k ∣ d j ) ∑ k = 1 K P ( w i ∣ z k ) P ( z k ∣ d j ) P(z_k|w_i,d_j) = \frac{P(w_i|z_k)P(z_k|d_j)}{\sum\limits_{k=1}^K P(w_i|z_k)P(z_k|d_j)} P(zk∣wi,dj)=k=1∑KP(wi∣zk)P(zk∣dj)P(wi∣zk)P(zk∣dj)
M 步:
P ( w i ∣ z k ) = ∑ j = 1 N n ( w i , d j ) P ( z k ∣ w i , d j ) ∑ m = 1 M ∑ j = 1 N n ( w m , d j ) P ( z k ∣ w m , d j ) P(w_i|z_k) = \frac{\sum\limits_{j=1}^N n(w_i,d_j)P(z_k|w_i,d_j)}{\sum\limits_{m=1}^M \sum\limits_{j=1}^N n(w_m,d_j)P(z_k|w_m,d_j)} P(wi∣zk)=m=1∑Mj=1∑Nn(wm,dj)P(zk∣wm,dj)j=1∑Nn(wi,dj)P(zk∣wi,dj)
P ( z k ∣ d j ) = ∑ i = 1 M n ( w i , d j ) P ( z k ∣ w i , d j ) n ( d j ) P(z_k|d_j) = \frac{\sum\limits_{i=1}^M n(w_i,d_j)P(z_k|w_i,d_j)}{n(d_j)} P(zk∣dj)=n(dj)i=1∑Mn(wi,dj)P(zk∣wi,dj)
给定文本集合,通过概率潜在语义分析,可以得到 各个文本生成话题的条件概率分布,以及各个话题生成单词的条件概率分布