Introduction to Linear Algebra 学习笔记(一)
笔者毕业后重拾线性代数的学习笔记,以 Introduction to Linear Algebra 第四版为教材
1.向量(Vector)的概念及其基本运算
为了方便进行线性代数里面的两个基本操作,即 vector addition (向量加法) 和 scalar multiplication(标量乘法,或称标量积),我们必须先引入一个基本概念那就是 Vector(向量,或称矢量)。只要具备基本中学物理知识,肯定都明白向量是什么东西。这是相对于标量而言的,所谓向量,就是既有大小(长度)又有方向的量;相对地,标量自然就是那些只有大小(长度)的量喽,我们平时肯定还是标量接触的比较多……emmmm……
在线性代数里,向量主要用 Column vector (列向量)的形式展示,比如我们现在有个含两个构成分量的向量 v 写出来就是下面酱紫:
v= [v1v2]
这里的这个向量有两个构成分量(即二维向量),即 v1 和 v2 。嗯没问题,我们继续往下走。
下面列举两个线性代数里面的基本操作,即vector addition (向量加法,就是向量的和运算) 和 scalar multiplication(标量乘法,或称标量积,就是向量的数乘运算)。我们以二维向量为例简单总结下这两种运算执行的操作。首先向量加法就是把两个二维向量的相应分量值线性相加从而得出一个新的向量:
vector addition:v = [v1v2] 和 w = [w1w2] 相加得 v + w = [v1+w1v2+w2]
注意向量加法满足交换律和结合律。
向量的数乘运算需要执行的的操作也很简单,就是把一个向量的各个分量与给定的标量线性相乘求出新的分量来组成一个新的向量~,以下:
scalar multiplication:2v = [2v12v2] and -v = [−v1−v2]
so. 向量的减法是什么样子的就无需多言了~
上面的例子,向量运算 scalar multiplication 里的 scalar 就是标量的意思,这里的scalar 分别是 2 和 -1,嗯。
向量这些基本运算的组合就叫做向量的 linear combination (线性组合)。具体定义:

tips:zero vector(零向量)
还是以我们这里列举的向量为例,假若用上面的向量 v 加上 -v,其结果是什么呢?当然是 [00] ,我们把这样的向量称为零向量,用一个单纯的数字 0 来表示零向量。
2.向量的可视化(向量的几何意义)
我们有三种表示向量的方法
- 两个数字的组合
- 坐标系中以原点(0,0)为起点的箭头(可视化的)
- 在坐标系中单纯戳个看得见的点(emmm……也是可视化的)
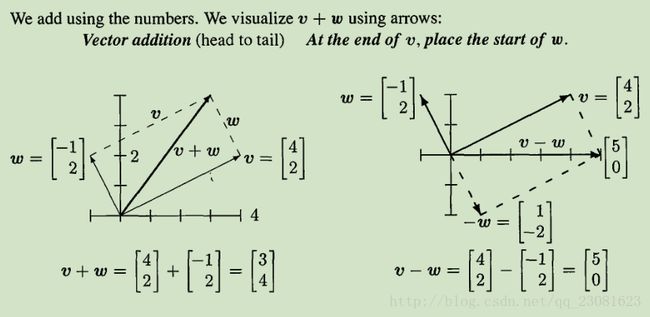
上面我们都是以第一种方法表示向量的,下面着重以第二种方式介绍下向量的可视化表示方法,就是坐标系中以原点为起点的箭头,呐就是下面这样子(这里你应该想到中学物理课本中合成 力 时的平行四边形法则和三角形法则,嗯,这就是向量加法的几何意义。那么自然向量的数乘运算就是向量长度的伸缩~):
ok基础里面最简单的二维向量就先说到这里~二维向量是基础知识里最简单的,然而越简单的东西越重要呢!后面的东西再难都是以这个最简单的东西为基础的,所以没事多拿出这篇笔记翻看下为好!
3.三维空间里的向量
二维平面里的向量很基础很简单,下面我们来认识下三维空间里的向量。
首先三维向量写出来是这样子滴
v = ⎡⎣⎢11−1⎤⎦⎥ 和 w = ⎡⎣⎢234⎤⎦⎥ 相加得 v + w = ⎡⎣⎢343⎤⎦⎥
这里有一个问题需要注意了,看上面图片里下面说的,就是为了表示起来简单我们把上面的向量 v 写成了 (1, 1, -1) 这样的形式。注意这里只是表示方法的问题,我们目前列举的向量都是列向量,也就是只有一列的那种比较简单的向量,这样横过来并把中括号替换成小括号并不是表示行向量的!这点要认识清楚。
三维向量的基本运算和二维向量是一致的,这里略过…
下面总结几个重要的点,就是比如现在有三个三维向量 u, v ,w,那么就有:
1. The combinations c**u** fill a line.
2. The combinations c**u** +d v fill a plane.
3. The combinations c**u** + d v + e**w** fill three-dimensional space.
嘿嘿都是书上原话,浅显易懂,我就不翻译了。
4.向量的点积(dot product)和长度(length)以及其他
- 向量的点积(dot product)又称为向量的内积(inner product)或数量积(scalar product),下面给出定义:
两个重要的不等式
首先,一个角的余弦值得绝对值是不会大于 1 的,再结合上面给出的公式我们可以得出第一个不等式,即 Cauchy-Schwarz 不等式:
第二个不等式即三角不等式,即一个三角形三条边的不等关系,比较好求证: