20200502:力扣185周周赛下
力扣185周周赛下
- 题目
- 思路与算法
- 代码实现
题目
思路与算法
-
数青蛙:本题考查一个模拟过程,把青蛙的叫声设计出croak五个过程,必须同时出现这5个,才是一个青蛙的叫声,否则返回-1。一开始想统计croak各自的数量,但是这题要求输出的是青蛙的数量。这样明显不行。举例2说明:这两只青蛙是可以同时开始叫的,或者在一只没叫完的时候就开始叫,一只结束之后再开始的话,视作同一只青蛙,仔细分析得:k为一个青蛙叫完的标志,且croak的顺序不能错,必须从c到k,因此我们遍历统计croak各自的数量即可,具体细节见代码。
-
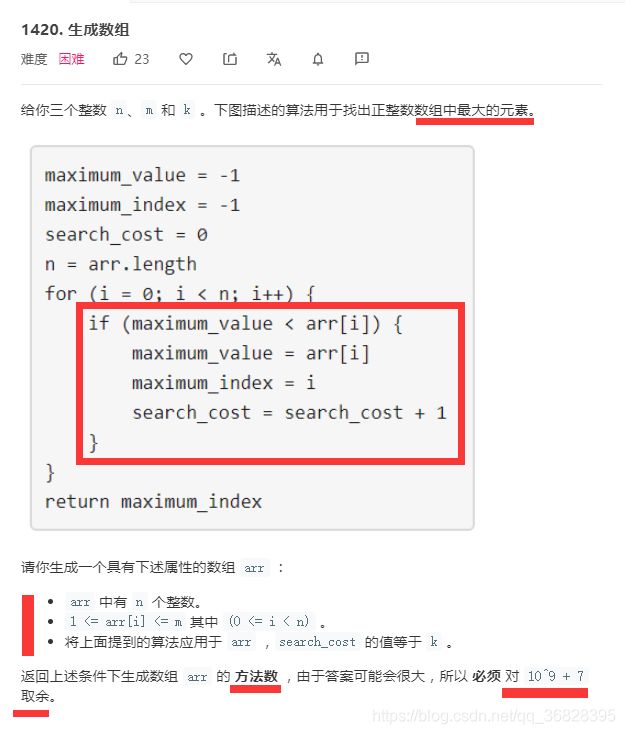
生成数组:举例1说明,n=2,m=3,k=1.
①.该数组有2个元素 ②.该数组的元素取值范围[1,3] ③.找到该数组的最大值搜索损耗为1,(从第一个元素开始搜索,需要1次就找到最大值,意味着数组的首字母为当前数组的最大值)读懂题目之后,基本不用再多想了,肯定是动态规划的范畴,只不过本题是一个三维动态,dp[i][j][p]:表示前i个元素最大值为j的情况下,搜索损耗为p,那么再将其分为两类,
①在这前i个元素中,第i个为最大值j,那么dp[i][j][p] = dp[i-1][x][p-1],其中x为1到j-1,每一种情况都加起来。 ②最大值在第1-第j-1个元素中,则最后一个元素可以为1-j的任意情况,dp[i][j][p] = j * dp[i-1][j][p]; 据此来写出代码即可。记得结果对1000000007取模
代码实现
- 数青蛙
class Solution {
public int minNumberOfFrogs(String croakOfFrogs) {
int res = 0;
int c = 0;
int r = 0;
int o = 0;
int a = 0;
int k = 0;
char[] frogs = croakOfFrogs.toCharArray();
for (char i : frogs) {
if (i == 'c') {
c++;
// 如果此时k不为0,说明有一个青蛙叫完了,则k--,意味 着不需要新的青蛙,刚刚叫完的上班即可。反之则需要新的青蛙,更新res即可。
if (k > 0) {
k--;
} else {
res++;
}
} else if (i == 'r') {
r++;
c--;
} else if (i == 'o') {
o++;
r--;
} else if (i == 'a') {
a++;
o--;
} else if (i == 'k') {
k++;
a--;
}
// croa出现小于0的情况,则说明顺序不对,跳出循环
if (c < 0 || r < 0 || o < 0 || a < 0) {
break;
}
}
// 最终如果都是croak成对出现,则croa一定为0,不为0,则返回-1,否则返回res
if (c != 0 || r != 0 || o != 0 || a != 0) {
return -1;
}
return res;
}
}
- 生成数组
class Solution {
public int numOfArrays(int n, int m, int k) {
final int MOD = (int)1e9 + 7;
long[][][] dp = new long[n + 1][m + 1][k + 1];
for (int i = 1; i < m + 1; i++) {
for (int j = 1; j < k + 1; j++) {
if (j > 1) {
dp[1][i][j] = 0;
} else {
dp[1][i][j] = 1;
}
}
}
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < k + 1; j++) {
if (j == 1) {
dp[i][1][j] = 1;
} else {
dp[i][1][j] = 0;
}
}
}
for (int i = 2; i < n + 1; i++) {
for (int j = 2; j < m + 1; j++) {
for (int a = 1; a < k + 1; a++) {
for (int b = 1; b < j; b++) {
dp[i][j][a] += dp[i - 1][b][a - 1];
dp[i][j][a] %= MOD;
}
dp[i][j][a] += j * dp[i - 1][j][a];
dp[i][j][a] %= MOD;
}
}
}
int res = 0;
for (int i = 1; i < m + 1; i++) {
res += dp[n][i][k];
res %= MOD;
}
return res;
}
}