分派问题(匈牙利算法)与MATLAB实现
一、分配问题
问题描述:有n项不同的任务,需要n个人分别完成其中的一项,由于各人去完成不同的任务所花费的时间(或费用)不同。于是产生了一个问题,应指派哪个人去完成哪项任务,使完成n项任务的所需时间最少。
二、匈牙利算法介绍
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法,并推动了后来的原始对偶方法。美国数学家哈罗德·库恩于1955年提出该算法。此算法之所以被称作匈牙利算法,是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。
其基本的理论基础是针对cost矩阵,将cost矩阵的一列或一行加上或减去一个数,求解最优任务的结果不变。
算法步骤:
第一步: 变换指派问题的系数矩阵,使 各行各列中都出现0元素
第二步:进行试分配,以寻求最优解。如果得到最优解,运算结束,否则转到第三步。
第三步:作最少的直线覆盖所有0元素。
第四步:变换矩阵(bi)以增加0元素,转到第二步。
三、匈牙利算法实例分析
利用匈牙利法解决如下任务分配问题。
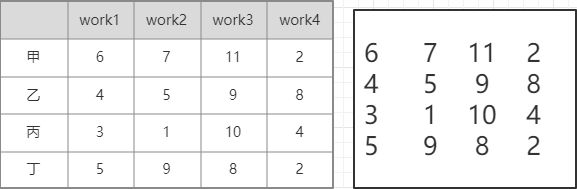
图为cost列表和cost矩阵。
第一步:将每行减去当前行的最小值(不一定是最小值,减去某一个值是为了让当前行中出现0元素,第二步的列同理)
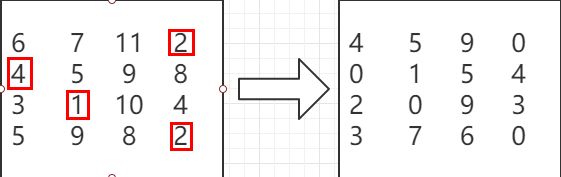
第二步:将每一列的值减去当前列的最小值
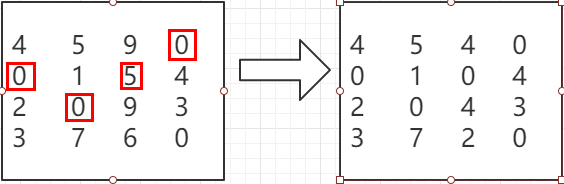
第三步:利用最少的水平线或者垂直线覆盖所有的0
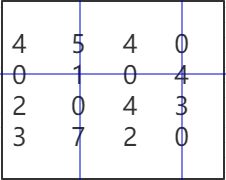
第四步:如果水平线和垂直线的总数小于4(矩阵的维度),则计算没有被覆盖的最小值,将没有被覆盖的每行减去最小值,被覆盖的每列加上最小值,然后跳转到步骤三。如果水平线和垂直线的总数等于4(矩阵的维度),则算法结束,得到分配结果。

第三步:利用最少的水平线或者垂直线覆盖所有的0
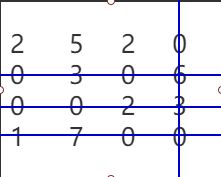
第四步:水平线和垂直线的总数等于4,算法结束,得到如下的分配结果
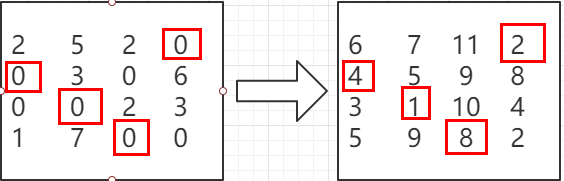
左边矩阵0元素的选取原则应该是一行和一列中只选取一个元素(即一个人只能工作一个任务),等价与右边的最优分配。
四、MATLAB实现
Hungary.m
function res=Hungary(N)
%输入的矩阵应N*N的
[a,~]=size(N);
%第一步每一行减去当前行最小值
for ii = 1:a
N(ii,:)= N(ii,:)-min( N(ii,:));
end
%第二步每一列减去当前列最小值
for ii = 1:a
N(:,ii)= N(:,ii)-min( N(:,ii));
end
num=0;
while num~=a
[num,N_min,del_hang,del_lie]=line_count(N);
if num ~=a
for ii=1:a
if del_hang(ii)~=ii
N(ii,:) = N(ii,:)-N_min;
end
if del_lie(ii)==ii
N(:,ii) = N(:,ii)+N_min;
end
end
else
res=N;
end
end
line_count.m
function [num,M_min,del_hang,del_lie]=line_count(M)
[a,~]=size(M);
num=0;
h=0;
del_hang=zeros(a,1);
del_lie=zeros(a,1);
for ii=1:a
del=ii-h;
[~,b]=size(find(M(del,:)==0));
if b>= 2
M(del,:)=[];
h=h+1;
del_hang(ii)=ii; %得到被覆盖的行数
num=num+1;
end
end
l=0;
for ii=1:a
del=ii-l;
[b,~]=size(find(M(:,del)==0));
if b >=1
M(:,del)=[];
l=l+1;
del_lie(ii)=ii; %得到被覆盖的列数
num=num+1;
end
end
M_min=min(min(M));
linear_assignment.m
function [place,res]=linear_assignment(M,N)
%N是n维矩阵,N是经过Hungary处理的
%M是未处理前的
[a,~]=size(N);
x=0;
place=zeros(1,a);
res=zeros(1,a);
judge=zeros(1,a);
while find(N==0)
for ii=1:a
judge(ii)=length(find(N(ii,:)==0));
end
judge(find(judge==0))=[];
if min(judge)==1
for ii=1:a
if length(find(N(ii,:)==0))==1 %先选出行中只有1个0
x=x+1;
place(x)=ii+(find(N(ii,:)==0)-1)*a; %得到矩阵中的位置
h=find(N(ii,:)==0);
N(ii,:)=1./zeros(1,a);
N(:,h)=1./zeros(a,1);
end
end
end
for ii=1:a
judge(ii)=length(find(N(ii,:)==0));
end
judge(find(judge==0))=[];
if min(judge)==2
x=x+1;
q=find(N==0);
place(x)=q(1);
N(mod(q(1),a),:)=1./zeros(1,a);
N(:,fix(q(1)/a)+1)=1./zeros(a,1);
end
end
[place,~]=sort(place);
for ii=1:length(place)
res(ii)=M(place(ii));
end
运行时代码:
A=[6 7 11 2;
4 5 9 8;
3 1 10 4;
5 9 8 2];
B=Hungary(A);
[~,b]=linear_assignment(A,B)
得到的结果:
b =
4 1 8 2
与前面分析的结果一致。