论文笔记: Quantifying Similarity between Relations with Fact Distribution

论文笔记: Quantifying Similarity between Relations with Fact Distribution

Author: Weize Chen, Hao Zhu, Xu Han, Zhiyuan Liu, Maosong Sun

Tsinghua, CMU

来源：ACL2019

链接:https://arxiv.org/pdf/1907.08937.pdf

动机

本文工作的核心目的是探究如何有效的量化关系的相似性。作者动作的动机是一个直觉，即关系的相似性和它对应的实体对有明显相关性，例如，关系为“trade to”或者”play for”的实体对通常为运动员和俱乐部，而“live”这种关系的实体对则通常为人和地点。作者将这个想法，进行了数学抽象，即将关系的相似转变为求解条件概率分布P(h,t|r)的相似度。对于分布相似度的求解，直接可以想到的就是利用KL散度。这里一个比较实际的问题是，KL散度在比较大的实体对空间里，基本不可解。考虑到这个因素，作者又提出了基于采样的算法来求解相应的KL散度。
在此基础上，作者希望通过设计和实验，更进一步讨论以下几个问题：

1. 根据本文算法计算的关系相似度相比人工判断有多大的差距？
2. 开放性的关系不可避免的会出现抽取关系的冗余，那么如何有效的减少冗余呢？
3. 量化相似度可以达到什么程度？用最好的关系抽取模型会发生相似性判断错误么？
4. 相似度计算有没有启发式的负采样算法？
5. 相似度可不可以作为关系抽取softmax-margin训练中的可适应性间隔呢？

形式化定义

在量化关系相似度之前，论文依据头尾实体的概率分布给出了关系的一个形式化的数学表达。首先定义一个映射：$F_{\theta }：ϵ\times R\times ϵ\to \mathcal{R}$，将一个三元组代表的关系事实 $(h,r,t)\in G=ϵ\times R\times ϵ$ 映射成一个标量，其中$ϵ$是实体集合，$R$是关系集合。 回到本文初始动机，从概率视角审视，将F函数看成r为参数，h,t为变量的二元函数，即$F_{\theta }(h,t;r)={\mu }_{\theta 1}(h;r)+{\mu }_{\theta 2}(t;h,r)$。 对于条件概率分布 ${\mu }_{\theta 1}$ 和 ${\mu }_{\theta 2}$可以通过神经网络去模拟，作为概率分布，我们需要再添加归一化，这样这个条件分布的表达如下:
$${\mu }_{\theta 1}(h;r)=log\frac{exp({\mu }_{\theta 1}(h;r))}{{\sum }_{h^{\prime }}exp({\mu }_{\theta 1}(h^{\prime };r))}$$

$${\mu }_{\theta 2}(t;h,r)=log\frac{exp({\mu }_{\theta 2}(t;h,r))}{{\sum }_{t^{\prime }}exp({\mu }_{\theta 2}(t^{\prime };h,r))}$$
$${\mu }_{\theta 1}(h;r)=ML{P}_{\theta 1}(r{)}^{T}h$$
$${\mu }_{\theta 2}(t;h,r)=ML{P}_{\theta 2}([h;r]{)}^{T}h$$
这样，$P_{\theta }(h,t|r)=exp({\mu }_{\theta 1}(h;r)+{\mu }_{\theta 2}(t;h,r))=exp(log\frac{exp({\mu }_{\theta 1}(h;r))}{{\sum }_{h^{\prime }}exp({\mu }_{\theta 1}(h^{\prime };r))}+log\frac{exp({\mu }_{\theta 1}(h;r))}{{\sum }_{h^{\prime }}exp({\mu }_{\theta 1}(h^{\prime };r))})$

这样loss function就被认为是是$P_{\theta }$的最大似然的负log，即
$$L(G)=\sum _{(h,r,t\in G)}-log{P}_{\theta }(h,t|r)$$

相似性量化

基于前面的形式化定义，本文假定可以通过计算概率$P_{{\theta }^{\ast }}(h,t|r)$的相似度来量化关系的相似度，这也和motivation里的基本直觉是一致的，即如果两个关系的实体对是相似的，那么这两个关系也相似；反正，则有较大差异。
那么如何衡量两个概率分布的相似度呢？ 自然的工具就是Kullback–Leibler divergence,即KL散度，$D_{KL}(P_{{\theta }^{\ast }}(h,t|r1)||P_{{\theta }^{\ast }}(h,t|r2))=E_{h,t\sim P_{{\theta }^{\ast }}(h,t|r1)}log\frac{P_{{\theta }^{\ast }}(h,t|r1)}{P_{{\theta }^{\ast }}(h,t|r2)}$
考虑到KL散度的非对称性，文中将关系相似定义为：
$$S(r1,r2)=g(D_{KL}(P_{{\theta }^{\ast }}(h,t|r1)||P_{{\theta }^{\ast }}(h,t|r2)),D_{KL}(P_{{\theta }^{\ast }}(h,t|r2)||P_{{\theta }^{\ast }}(h,t|r1)))$$
函数 g(x,y)是一个人工定义的函数来修正对称性，因为相似度的取值为非负，且满足单调递减，所以指数族是一个好的选择，本文选取的是 $g(x,y)=e^{-max(x,y)}$

表1 关系量化方式一览

表一对比了本文和之前其他工作的关系相似度量化方式，可以看出其他方式情形将关系编码成向量，然后通过计算向量的相似度。本文认为之所以直接使用分布的差异来量化关系而不是比较关系编码后的向量，有两个原因：1）关系Embedding的过程中会丢失很多细节；2）用分布差异来量化，可解释性强。以图1为例，两个关系“be an unincorporated community in”(蓝色点)和“be a small city in”（红色点）。点的坐标是通过T-sne将采样的实体点的Embedding降维之后级联的，两个大的点，是通过TransE编码的关系向量。可以看出，编码后的关系在向量空间中比较接近，但是两个关系其实差异还是比较明显的，从实体的分布可以较为清晰的看出。

图1 关系量化方式对比差异示例

采样方法

实际到此为止，整个论文的思路已经较为完成，但是具体去实现，还差了最后一环，在一个大数据集或者开放域环境中，KL散度的计算需要遍历所有样本空间，因而是不可解的。 解决这个问题的方法，自然是利用采样来实现，本文使用的是蒙特卡洛方法。具体如下：
$$\begin{gathered} D_{KL}(P_{{\theta }^{\ast }}(h,t|r1)||P_{{\theta }^{\ast }}(h,t|r2)) \\ =E_{h,t\sim P_{{\theta }^{\ast }}(h,t|r1)}log\frac{P_{{\theta }^{\ast }}(h,t|r1)}{P_{{\theta }^{\ast }}(h,t|r2)} \\ =\frac{1}{|S|}\sum _{h,t\in S}log\frac{P_{{\theta }^{\ast }}(h,t|r1)}{P_{{\theta }^{\ast }}(h,t|r2)} \end{gathered}$$
S是根据概率$P_{{\theta }^{\ast }}(h,t|r1)$抽样得到的实体对，具体操作时采用序列抽样的方式，即首先依概率${\mu }_1$抽样h, 在根据h依概率${\mu }_2$抽样t。

数据集构建

本文使用了三个数据集，wikipeda (实体来自item，使用Reverb自动抽取，去掉特别高频的关系，使数据集均衡)，FB15k （Freebase的子集），TACRED （较大规模的有监督关系抽取数据集），参见表2。

表2 本文使用的数据集

实验和讨论

通过实验验证本文最初提出的几个关键问题：

1. 根据本文算法计算的关系相似度相比人工判断有多大的差距？
   本文通过了9个本科生进行人工标注，去衡量从wikipeda中抽取的360个关系对的相似性，并进行打分。打分原则：
   4分， 两个关系完全等价，如 （study at, be educated at)
   3分， 两个关系描述同一个主题，且关联的实体类型相同，如 (be the director of, be the screenwriter of)
   2分， 两个关系描述同一个主题，但实体类型不同，如 (be headquartered in, be founded in)
   1分， 仅有语义的联系，如 (be the developer of, be the employer of)
   0分， 毫不相关，如 (be a railway station locates in, be published in)
   以Spearman 相关系数作为指标，对比本文的方法和其他4个基线方法，可以看出，本文的方法明显更接近人类的判断，可以达到0.63左右，如图2所示
   

图2 Spearman correlations between human judgment and models’ outputs

2. 开放性的关系不可避免的会出现抽取关系的冗余，那么如何有效的减少冗余呢？
   有效减少开放域关系抽取带来的冗余，是本文提出的关系量化的一个重要应用。为了验证效果，本文设计了一个玩具实验和真实数据实验来进行验证。
   玩具实验：
   应用中国餐馆过程从wiki中抽取关系，并将其分成若干个子关系。具体来说，对于一个关系r，它当前已经有m个子关系了，对于一个新的r的实例，将其划分为一个新的子关系的概率为$p=\frac{\alpha }{\alpha +n+1}$, 而将它划分为已知的第k个子关系的概率为$p=\frac{n_k}{\alpha +n+1}$。其中$\alpha$是超参宿，文章中取值为1，$n_k$为第k个子关系的实例数，$n$为r的所有子关系的实例数。然后过滤掉所有实例数少于50的子关系，共计得到所有关系1165个。在此基础上，应用关系相似度的量化方法进行关系合并，最终得到的结果如表3所示。可以看出本文的方法在Open IE去除冗余的过程中有明显的优势。
   

表3 The experiment results on the toy dataset

3. 量化相似度可以达到什么程度？用最好的关系抽取模型会发生相似性判断错误么？
   对于真实数据集的评估，本文采用ReVerb构建数据集，在训练的时候不同的模式就当成是不同的关系，然后进行关系合并。因为对于真实数据集，无法遍历数据集来构建准确率和召回率这样的评价指标，作者在这里使用了拒绝采样和重要性采样的技巧，去构建评价指标，最终的结果如图3所示。可以看出本文的算法在准确率较高的情况下,可以达到一个比较高的召回率. 这里对于评价指标的定义如下:
   $$Recall=E_{x\sim U}I[\hat{f}(x)=1]\approx \sum _{i=1}^{n}I[\hat{f}(x_i)=1]\widehat{w_i}$$
   $$Precision=E_{x\sim U^{\prime }}I[f(x)=1]\approx \frac{1}{n}\sum _{i=1}^{n}I[f(x_i)=1]$$
   其中, $x=(r1,r2)\in R\times R$代表一对关系实例,$f(x)\in 0,1$ 代表 $x$ 的label, 及表示关系r1和r2是同一个关系;$\hat{f}(x)$ 是对于$x$的预测,即$S(r1,r2)>阈值\lambda$。分布U 是从所有 $f(x)=1$的样本的一个均匀分布; U’是$\hat{f}(x)=1$的样本的一个均匀分布。$\widehat{w_i}$代表样本重要性。
   

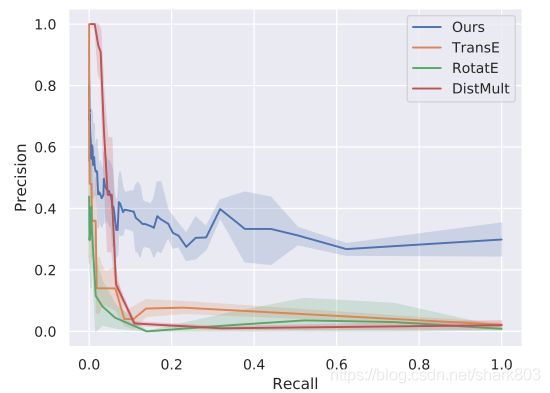
图3 Precision-recall curve on Open IE task

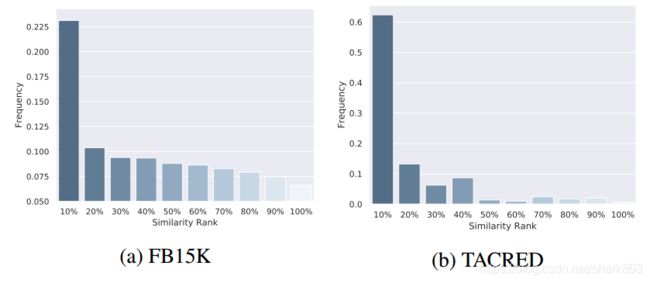
对于第二个问题，图4显示了模型的输出在关系预测和关系提取任务上的分散关系的相似性等级分布。 从图4a和4b中，我们可以观察到最具干扰性的关系是最相似的关系，这也说明：即使在这些任务上的最佳模型在最相似的关系中仍然会犯错误，同时也反映了启发式方法对指导模型更加关注相似关系之间的边界的重要性。

图4 Similarity rank distributions of distracting relations on different tasks and datasets

4. 相似度计算有没有启发式的负采样算法？
   本文尝试使用关系类型约束进行负采样，但是与统一采样相比，看不到任何改进。具体参考论文的附录E部分。 论文的第8节讨论了应用容易混淆的关系来进行负采样，效果如图5所示。

图5 Improvement of using similarity in a heuristic method for negative sampling

5. 相似度可不可以作为关系抽取softmax-margin训练中的可适应性间隔呢？
   可以将相似度作为一个可适应的margin 纳入softmax-margin, 将原来loss中的关系相似代价如， $cost(r^{(i)},r)$替换成$\alpha S(r^{(i)},r)$. 表4 证明关系模型的整体表现还是有一定幅度的提升。
   

表4 Improvement of using similarity in softmaxmargin loss

其他

本文有一个关于前面recall的证明非常的精彩，很好的应用了拒绝采样，重要性采样和自正规化技巧，具体参见论文附录A。