本文来自北京润乾软件技术有限公司董事长蒋步星在清华大数据产业联合会的讲座。
下面我们来讲关系代数中的具体的问题,先谈关联运算的描述。
使用SQL对于单表进行查询并不是很难理解和实施,一般也就是选取字段、过滤、排序等,只有分组汇总稍复杂些,也不是多难懂。
但是,有意义的查询经常是多表的,比如查一下从北京到上海打了多少电话,存款超过10万元的人中本科学历及以上的有多少。这些都需要用到多表关联运算。
SQL中用多表关联运算是用JOIN运算实现的,JOIN运算在关系代数中定义非常简单通用,就是两个表做笛卡尔积后再过滤。
简单的好处,就是适用面广,什么都能表达;但也有坏处,它没有把更多的运算特征体现出来。这样,对于关联复杂的情况,无论是理解还是实施都很困难。类比一下,四则运算中如果只有加法没有乘法显然会很头疼。虽然乘法都可以用加法表达,但实在很麻烦。
实施运算也麻烦,我们有九九表算乘法,不需要硬加起来就可以快速运算。要按关系代数的定义来实现JOIN运算也会有类似的困难,当然数据库厂商实施的时候都会做工程上的优化,我没有见过哪个厂商真地用笛卡尔积实现一般的等值JOIN运算,但要严格地实现这个定义,还是会给工程上优化造成很大困难。
- 外键引用
- 同维对齐
- 汇总对齐(特殊的同维对齐)
事实上,仔细分析后,我们会发现,实际应用中大多数的JOIN都是上面这三种情况,而不需要引入笛卡尔积。
这里说大多数,不是全部,就象不可能把所有的加法都可用乘法来表示。仍然有一些关联运算需要用原始的JOIN来描述,比如用SQL做矩阵乘法,就需要用笛卡尔积。
但日常数据分析中的大多数JOIN都属于这三种情况,我们逐个来解释。
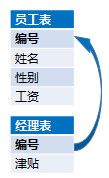
首先是外键属性化,先来看一个例子:
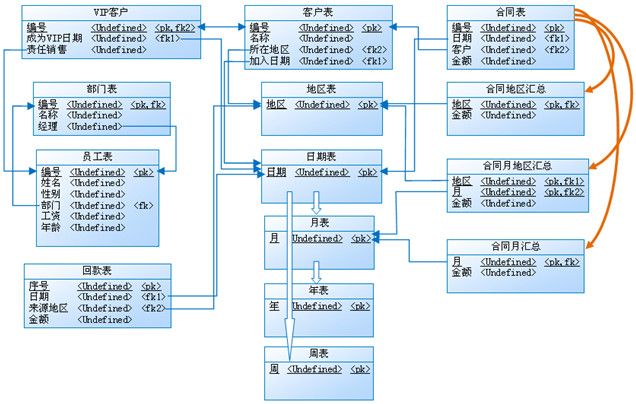
这里有两张表,一个员工表,一个部门表,我们想查一下中国经理的美国员工。员工表里面有一个字段叫部门,这是个外键指向部门表的主键。部门表里又有一个经理字段指回员工表。这是一个很常见的数据结构设计,指来指去的。
我们要算中国经理的美国员工,SQL写出来是这样的:
员工表和部门表JOIN起来,再JOIN回员工表,也就是要同表自叉乘,需要起个别名。在WHERE中先写上JOIN的条件,和最终我们希望的条件,一个国籍是中国,一个国籍是美国。整个句子要看一会才能明白。
这是我的招聘考题,通过率不到一半。许多还都是有两三年工作经验的。不到一半的通过率,可想而知它还是有一定难度的。
那么,为什么不能这样写呢?我还是说员工表,美国员工好理解,但是中国经理这件事我把它写成这样,就是上面红色的部分,这个字段稍复杂一点,有子属性,子属性又有子属性,但那一小段语句并不难理解,也就是部门的经理的国籍是中国。
也就是说,我们要:
(1) 外键指向表的字段可直接引用
(2) 允许多层和递归引用
SQL不是这样理解外键的,而我们这样去理解外键就容易多了,外键指向的属性可以被直接引用,也可以多层引用,这样就会简单得多,把外键看成一种属性,把JOIN这个运算不再简单地理解成笛卡尔积加过滤。这是第一种情况。
第二种情况是同维表等同,这个比较简单。
这两个1:1的表,主键相同,在数据库设计中经常会有这种情况,许多字段都放在一个表里太宽,还会造成空间冗余浪费,导致性能下降,因此常常会分到多个主键相同的同维表中。
现在我们要做联合查询,这又得做JOIN。
我们希望能把它看成同一个表,直接这么写:
![]()
还是看红色的部分,同维表的字段可以在任何一个表中随意访问。也就是(1)主键同维的表将视为一个宽表;(2)访问其中任何一个均可引用其他字表的字段。
这样也会让关联变得简单一些,不必再理解这种JOIN。
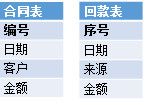
第三种情况,按维汇总对齐
这里有合同表和回款表,我们希望按日期统计合同额与回款额,用SQL写出来是这样的:
先把每个表分组汇总后再JOIN起来,如果偷懒不用子查询先JOIN后GROUP,那结果是错误的,统计值会变多。这个问题必须使用子查询。
能不能再简单一些呢?我们可以写成这样:
注意红色的部分,我们只要把两个表分别按日期对齐就行,这两个表之间并没有直接关联。我们不必关心表间关联,各自独立计算各自的数据就可以了。
如果这个事情再扯到外键的事就会更复杂,比如:
我们希望按地区统计销售员人数和合同额,用SQL写出来是这样:
这个子查询中要套着带JOIN的GROUP,更复杂了。
类似地,按我们刚才的写法结合第一种情况的外键处理方法,这个查询可以写成这样:
红色部分中出现了子属性,但整个句子仍然很简单。
这一条总结起来就是:
- 每表独立设定统计维度,无须关心表间关联;
- 可按外键属性对齐。
三种常用的JOIN以及简化方式说完了,这样理解数据关联有什么用处呢?
一个应用就是用来实现自助报表,或者OLAP。
我是做报表工具出身的,用户经常会向我们提出业务人员自己做报表的需求,自助报表的关键在于让用户把需要的数据取出来,而取数的关键又在于解决多表关联,就如前面所说,有意义的查询大多是多表关联的。把蜘蛛网式的表间关联呈现给业务用户,有时候还需要自关联,要用别名,我想大多数业务人员会晕掉的。
传统的OLAP工具是如何解决多表关联问题呢?
一般都是采用事先建模的方式,要预测用户可能以哪种关联方式查看数据表,事先将关联做成物理宽表或者逻辑视图,这样用户看到就是一个单表了。这是典型的按需建模,也就是有了新的关联需求时就需要再建一个视图或宽表,而建模需要技术人员完成,这个过程的周期就会很长。
有些传统OLAP工具能够根据维的类型自动关联,但解决得不彻底,当同一个表中出现多个同维字段时就会对不上了,比如一个学生有出生地和入学地,都是地区维度,就不知道该怎么自动对应了。对于自关联的处理也很麻烦,需要事先约定指向路径,其实还是按需建模。
如果关系代数对关联的处理是我们上面简化的那样,就不需要这么麻烦了,那三种情况能够描述的关联占了大多数,对自助报表和OLAP业务几乎是全部了,这类关联只要一次性建模就可以了。
也就是说,能达到这样的效果:
- 从按需建模到一次性建模
- 从单星模型到多雪花模型
- 隐藏表概念,无须理解关联
我们按照上述模型开发了一个语法翻译引擎,把上面那种简单语法翻译成完整的SQL交由数据库去执行。在这个基础上,配上一个界面就可以方便地实现自助报表。
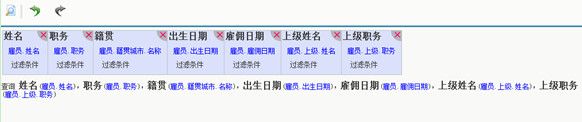
这是选择数据项的界面,不需要涉及到表的概念,只是数据项稍复杂些,有子数据项,数据项的组织呈树状,不象平常的数据字典是线状的,这个树的层次关系就体现了表的外键关系。
做报表时,我只要把需要的数据项往表里拽就行了。
这和普通单表取数没太大区别,无非就是字段有多层子属性。
这个界面生成上面看到的那些简单语法是很容易的,然后再翻译成SQL执行就可以了。
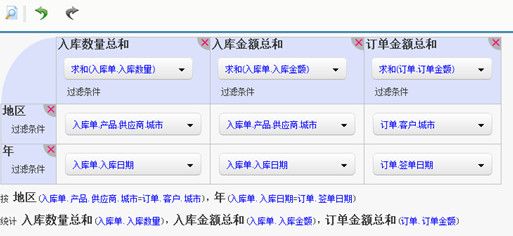
在做汇总报表时也很简单,把汇总用的维度选定后,仍然是把要统计的数据项往表里拖就可以了。
你不必关心这些数据项来自哪些数据表,这些数据表之间有什么关联。
这样看待关联还有个好处,就是数据库的结构更清晰:
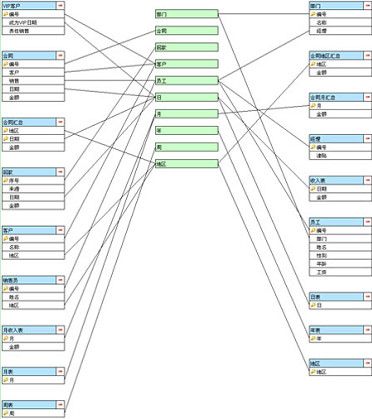
这是我们平常的ER图,网状结构的,表和表之间都有关系,表多了就很乱,表间耦合度高,加删表时可能牵一发动全身。
而用刚才那种方式理解表间关联,看到的结构是这样一种总线式的:
表和表之间没有直接关联,互相没有耦合,表只和中间的维度关联,增加删除表时不影响其它表。
需要说明的是,结构图中连线数量并不因为样式变了而变少,这是数据本身的关联特性决定的,但后一种画法会让结构更清晰了。
这种关联机制在性能方面也有优势。大家知道SQL做分布式计算是很难的,而难就难在JOIN,其它GROUP、WHERE都很容易分布并行计算。但如果把JOIN看成刚才说的那几种情况,分布式计算时就会容易许多。
在这几种JOIN中,同维对齐的表可以按同样规则分段存储,这样就很容易分布了;外键指向的维表不能同步分段,但一般维表会较小一些,可以在每台机器都存储一份,甚至可以在内存中放下,这样可以用冗余数据换取性能,大的事实表再分段存放,这时JOIN计算几乎不需要发生跨机关联了。
关系代数不区分这些JOIN类型,必须实现笛卡尔积式的JOIN运算,分布式计算就困难的多,一般的办法是将表按键值HASH到不同节点机上再计算,造成大量的网络传输。
不同的JOIN还可以用不同的方法去优化。同维对齐可以事先排序再用归并算法,这个复杂度要比HASH JOIN小得多。外键连接,如果内存可放下则可用指针去做,外存也可以事先转换成序号直接快速定位。
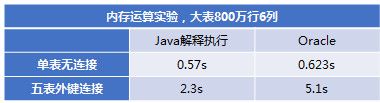
当然实际实现起来事还不少。我们目前只做了内存实验。用JAVA的计算与ORACLE对比,采用数据量比内存小,这样ORACLE会把数据都缓存到内存中。
我们不必看JAVA和ORACLE的对比,技术不一样,一个纯内存,一个有外存。我们只看两者比值的变化,无连接运算的单表,耗时差不多。五个表JOIN时,JAVA用指针连接的方式比ORACLE的HASH JOIN快了一倍多。这种技术放在外存上也会有优势。