机器学习系列(21)_SVM碎碎念part4：无约束最小化问题

原文地址：SVM - Understanding the math - Unconstrained minimization by Alexandre KOWALCZYK
感谢参与翻译同学：@田苗苗 && @樊睿 && @jozee
时间：2018年1月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/70214565
声明：版权所有，转载请联系寒小阳 ([email protected])并注明出

1.引言

这是SVM系列教程第4部分。接下来我们学习如何求解无约束极小值问题。如果你之前没有读过之前的文章，建议从《SVM碎碎念1》开始学习。

2.本部分内容

这部分内容涉及面很广，需要很多的预备知识。所以我花了很多时间来规划学习路线，决定哪些知识应该解释，而哪些知识可以略过。由于最终的内容过于庞大不便于阅读，我便把它拆分成3个部分，分别为Part4，Part5，Part6！

在Part4的中，我尽可能的把内容讲得简洁明了。这里假设大家已经具备了导数和偏导数的相关知识。同时，也希望你们具备了矩阵变换，计算矩阵行列式的相关知识。

在过去的几个月里，我收到了很多意见和鼓励。这篇文章的发布之时，已经有好几百人订阅了这个系列的文章。谢谢你们所有人，希望你们读的开心！

3.从哪里着手

在第3部分中，我们知道最大化间隔就是最小化w的模。

这意味着我们需要解决以下最优化问题：

最小化(w,b)∥w∥约束条件为 yi(w⋅xi+b)≥1(约束条件对任意的i=1,…,n都成立)

首先需要注意的是该最优化问题带有约束条件。它们是由“约束条件为”开头的行来定义的。这里并不是你所想的，只有一个约束条件，而是有 n 个约束条件。（因为最后一行表示任意 i =1,…, n ，约束条件都成立）

“那么，如何求解这类问题？自第3部分之后大家就一直在等解决方案！！！”

在处理如此复杂的问题之前，让我们先从一个稍微简单的问题入手。我们先来看看如何求解无约束最优化问题，准确的来说，是求解无约束最小化问题。问题的关键在于找到使得函数返回最小值的输入值。(注意：在SVM问题中，就是求 w 二范数的极小值，把 w 二范数叫做 f ，记作 f(w)=∥w∥ )。

4.无约束最小化问题

首先定义一个变量 x∗ (读作“x 星”，添加一个星号以便知道我们讨论的是一个特定的变量，便于跟 x 区分开)。

我们如何知道 x∗ 是否是函数 f 的一个局部极小值点？很简单，我们只需要应用以下的定理：

定理:

令 f ： f：Ω→ℝ 在 x∗ 处二次连续可微。

如果 x∗ 满足 ∇f(x∗)=0 以及 ∇2f(x∗)=0 是正定的，那么 x∗ 就是一个局部极小值点。

(定理证明 ，第11页)

尽管上面的定理非常简洁，但是如果没有相关的背景知识，那么理解上面的定理几乎是不可能的。比如， ∇f(x∗)=0 是什么？ ∇2f(x∗)=0 是什么？正定又是什么？

那我们就给出更多信息的定义详细说明：

定理(更详细):

如果 x∗ 满足以下条件:

1. f 在 x∗ 处梯度为0:
   

   ∇f(x∗)=0
   
   以及

2. f 在 x∗ 处的Hessian(海森矩阵)是正定的:
   

   (zT)((∇2f(x∗))z>0,∀z∈ℝn
   
   此处
   ∇2f(x)=⎛⎝⎜⎜⎜⎜⎜⎜∂2f∂x21⋮∂2f∂xn∂x1⋯⋱⋯∂2f∂x1∂xn⋮∂2f∂x2n⎞⎠⎟⎟⎟⎟⎟⎟
   
   ​

那么， x∗ 就是一个局部极小值点。

4.1 这些都是什么意思？

让我们逐步检验这个定理。

步骤一:

令 f : Ω→ℝ 在 x∗ 处二次连续可微。

首先，让我们介绍一下函数 f ，这个函数从集合 Ω 中取值并返回一个实数。这里的第一个问题，就是没有告诉 Ω 是什么，不过我们将在步骤二中揭晓。函数 f 应该是连续的且二次可微的，否则定义的其他部分将不成立。

步骤二:

x∗ 是 f(x) 的局部极小值点，当且仅当:

我们希望找到一个点让 f 取到极小值。我们将这个点定义为 x∗ 。

从符号中我们可以看出两点:

1. x∗ 用粗体书写，所以它是一个向量。这意味着 f 是一个多元函数
2. 集合 Ω 是函数 f 的定义域。从而得出， Ω 的集合元素是向量，而且 x∗∈Ω ( x 星属于 Ω )。

步骤三:

f 在 x∗ 处梯度为0

如果希望 f(x) 在 x∗ 处取到局部极小值，那么在 x∗ 处梯度为0是第一个必须满足的条件。我们必须验证函数 f 在 x∗ 处的梯度是否为0。什么是梯度？它就类似于一元函数的导数。

定义:”梯度是导数概念从一维空间向多维空间的推广(泛化)” (维基百科)

这个定义给了我们更多的信息。事实上，梯度跟导数的核心思想是一样的，只不过函数 f 的输入值为向量。这也是为什么开始的时候要求函数 f 是可微函数。如果没有这个前提条件，我们就没法计算梯度，整个求解过程也无法继续进行下去了。

在微积分中，当我们想要研究一个函数时，通常我们会求出函数导数并判断导数的正负情况。这能让我们知道这个函数是递增的还是递减的，从而确定函数的最大(最小)值点。通过让导数为0，我们可以找到函数的”临界点”，在这个点处函数取最大(最小)值。(如果想回顾，请阅读这里更加完美的解释)。当目标函数是多元函数时，我们需要让目标函数的每一个偏导数为0。

综上所述，函数的梯度就是函数所有的偏导数组成的向量。通过判断梯度的正负情况，我们就能得到函数的重要信息。在这种情况下，如果 x∗ 是一个临界点(函数 f 很可能在这个点处取极小值)，我们需要验证函数梯度在 x∗ 处是否为0。(注意:检查某点的梯度是否为0就是检查该点的所有的偏导数是否等于0)。

函数梯度由符号 ∇ 来表示。

如下

∇f(x∗)=0

是数学中” f 在 x∗ 处梯度为0”的符号表示。

对于向量 x∗(x1,x2,x3) ，∇f(x∗)=0 表示:

∂f∂x1(x∗)=0∂f∂x2(x∗)=0∂f∂x3(x∗)=0

步骤四:

函数 f 在 x∗ 处的Hessian(海森矩阵)是正定的

这里很多人会比较迷糊。虽然只是简单的一句话，却需要很多背景知识。需要知道:

1. Hessian(海森矩阵)是一个二阶偏导数矩阵
2. 如何判定一个矩阵是正定的

4.2. Hessian(海森矩阵)

Hessian是一个矩阵，也叫海森矩阵。我们可以称它为 H ，但是这里使用 ∇2f(x) 来表示更加直白些。我们使用 ∇ 表示梯度，加上一个 2 来表示二阶偏导数矩阵。我们将从函数 f 中计算出这些偏导数。通过 f(x) 可以知道，函数 f 的输入值是向量 x 以及 根据给定的 x 计算Hessian(海森矩阵)。

综上所述，我们需要计算一个矩阵，该矩阵为在 x∗ 处的Hessian(海森矩阵)。

已知函数 f ， x∗ 的值，根据以下Hessian(海森矩阵)的公式，计算出矩阵中的每一个元素。

∇2f(x)=⎛⎝⎜⎜⎜⎜⎜⎜∂2f∂x21⋮∂2f∂xn∂x1⋯⋱⋯∂2f∂x1∂xn⋮∂2f∂x2n⎞⎠⎟⎟⎟⎟⎟⎟

最终我们得到Hessian矩阵，它包含了我们计算的所有数值。

让我们看看Hessian(海森矩阵)的定义，看看我们是否有很好的理解：

定义:在数学中，Hessian矩阵或者Hessian 是一个多变量实值函数的二阶偏导数组成的方阵。它描述多元函数的局部曲率。

(注意:标量值函数的输入是一个或多个值，但返回单个值。在我们的例子中，函数 f 是一个标量值函数 。)

4.2.1 正定性

现在我们得到了Hessian矩阵，我们想知道其在 x∗ 处是否是正定的。

定义:如果对称矩阵 A 满足 xTAx>0 ，对所有的 x∈ℝn 都成立。对称矩阵 A 被称为正定矩阵。(来源)

请注意，这里我们再次给出了Hessian(海森矩阵)正定的定义。由于数学符号比较抽象，阅读起来有点困难。如果我们使用 ∇2f(x∗) 代替 A ，用 z 代替 x ，我们就得到了在前面定理第二部分写的公式:

zT((∇2f(x∗))z>0, ∀z∈ℝn

这个定义的问题在于它讨论的是一个对称矩阵。对称矩阵是一个方阵，它等于它的转置。

Hessian是一个方阵，但是否是对称矩阵呢？

很幸运，它是对称矩阵！

“如果函数 f 的二阶偏导数在邻域 D 中是都是连续的，那么函数 f 的Hessian(海森矩阵)在邻域 D 中就是一个对称矩阵”(维基百科)

但即使有了这个定义，我们仍然不知道如何检查Hessian是否是正定的。因为公式 zT((∇2f(x∗))z≥0 是对在 ℝn 中所有 z 来说的。

我们不能穷尽 ℝn 中的所有的 z 。

这就是为什么我们要使用下面的定理：

定理:

以下的表述是等效的:

• 对称矩阵 A 是正定的

• A 的所有特征值都是正的

• A 的顺序主子式都是正的

• 存在非奇异方阵 B ，使得 A=BTB

  (来源)

所以我们有三种方式检查一个方阵是否是正定的:

• 通过计算它的特征值并检查它们是否是正数。
• 通过计算它的顺序主子式，并检查它们是否是正的。
• 通过找到一个非奇异方阵 B ，使得 A=BTB 。

让我们使用第二种方法并且进一步更加详细地理解它。

4.3. 计算顺序主子式

4.3.1 子式

计算矩阵的子式 Mij ，首先移除矩阵的第 i 行和第 j 列，然后计算剩余矩阵的行列式即可得到子式 Mij 的值。

举例:

让我们考虑以下 3×3 矩阵:

⎛⎝⎜⎜adgbehcfi ⎞⎠⎟⎟

为了计算这个矩阵的子式 M12 ，我们删除了第一行和第二列。我们得到:

⎛⎝⎜⎜◻dg◻◻◻◻fi⎞⎠⎟⎟

然后我们计算的剩余矩阵的行列式:

(dgfi)

值为: di−fg

4.3.2 主子式

当 i=j 时，子式 Mij 被称为主子式。

对于 3×3 矩阵来说，它的主子式为:

• M11=ei−fh ,
• M22=ai−cg
• M33=ae−bd

但是，这不是全部！事实上，子式也有我们所说的阶。

定义:

如果通过删除 n−k 行和删除对应编号的 n−k 列得到 k 阶子式 ，则我们称它们为矩阵 A 的主子式。(来源)

在前面的例子中，矩阵是 3×3 的，所以 n=3 ，我们删除了1行和一列，从而得到了2阶主子式。

有 (nk) 个 k 阶主子式，并把 k 阶主子式表示成 Δk

综上所述:

Δ0 : 不存在，因为如果同时删除三行三列，相当于删除了整个矩阵。

Δ1 : (3−1)=2 ，就是说我们同时删除2行和相同编号的2列得到的主子式。

所以我们删除了第一行和第二行，第一列和第二列，得到:

⎛⎝⎜⎜◻◻◻◻◻◻◻◻i⎞⎠⎟⎟

这意味着1阶的主子式之一是 i 。同样我们可以找到其他主子式:

我们删除第二行和第三行，第二列和第三列，我们得到 a 。

我们删除第一行和第三行，第一列和第三列，我们得到 e

Δ2 : 就是我们之前看到的:

• M11=ei−fh ,
• M22=ai−cg
• M33=ae−bd

Δ3 : 我们什么都不删。所以它是矩阵的行列式:

aei+bfg+cdh−ceg−bdi−afh 。

4.3.3 顺序主子式

定义:

矩阵 A 的 k 阶顺序主子式是指 删除矩阵 A 最后的 n−k 行和最后的 n−k 列而得到的 k 阶主子式。

由此可见，顺序主子式更容易得到。如果我们记 k 阶顺序主子式为 Dk ，我们可以得到:

D1=a (我们删除了最后两行的最后两列)

D2=ae−bd (我们删除了最后一行和最后一列)

D3=aei+bfg+cdh−ceg−bdi−afh

现在我们可以计算一个矩阵的所有顺序主子式。我们来计算在 x∗ 处的Hessian(海森矩阵)的所有顺序主子式，如果它们都是正数，我们就知道该Hessian(海森矩阵)在 x∗ 处是正定的。

到目前为止，我们已经解释了所有必备知识，那么你们应该能够理解求解无约束最小化问题。接下来，让我们举例说明。

4.3.4 举例

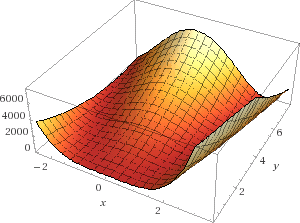
在这个例子中，我们将试图找到如下函数的最小值: f(x,y)=(2−x)2+100(y−x2)2 ，这个函数叫做 Rosenbrock 香蕉函数。(函数表达式为 f(x,y)=(a−x)2+b(y−x2)2 )

Rosenbrock 香蕉函数  a=2， b=100

首先，我们要找到使梯度 ∇f（x，y） 等于0的点。

∇f(x,y)=⎛⎝⎜⎜⎜∂f∂x∂f∂y⎞⎠⎟⎟⎟

我们计算偏导数，可发现：

∂f∂x=2(200x3−200xy+x−2)∂f∂y=200(y−x2)

（提示：如果你想验证你的计算结果，你可以使用数学搜索引擎 Wolfram alpha)

我们的目标是找到使所有偏导数为0的点，所以我们需要解下面的方程组：

2(200x3−200xy+x−2)=0(1)

200(y−x2)=0(2)

我们展开得到:

400x3−400xy+2x−4=0(3)

200y−200x2=0(4)

我们将 (2) 式乘以 2x 得到:

400xy−400x3=0(5)

我们把 (3) 式加上 (5) 式得到:

400x3−400xy+2x−4+400xy−400x3=0(6)

此式可以简化成:

2x−4=0x=2

我们将 x 带入 (4) 式得到

200y−200×22=0200y−800=0y=800200y=4

我们已经找到了使 ∇f(x,y)=0 的点 (x,y)=(2,4) 。但问题是这是极小值点吗?

Hessian(海森矩阵)为:

∇2f(x,y)=⎛⎝⎜⎜⎜⎜∂2f∂x2∂2f∂x∂y∂2f∂x∂y∂2f∂y2⎞⎠⎟⎟⎟⎟∂2f∂x2=1200x2−400y+2∂2f∂x∂y=−400x∂2f∂y∂x=−400x∂2f∂y2=200

现在计算 (x,y)=(2,4) 点的Hessian矩阵

∇2f(x,y)=(3202−800−800200)

矩阵是对称的，我们可以检查它的顺序主子式：

1 阶顺序主子式：

如果我们删除最后一行，最后一列得到主子式 M11 是 3202 。

2 阶顺序主子式：

即Hessian(海森矩阵)的行列式：

3202×200−(−800)×(−800)=400

Hessian(海森矩阵)的所有顺序主子式都是正数。这意味着Hessian是正定的。
我们所需要的两个条件得到了满足，这时我们可以说点 (2,4) 一个局部极小值点。

4.4 局部极小值？

在指定的取值范围内，函数在某个点处的值为最小值时，那这个点可称为局部极小值点。其严格定义如下：

给定函数 f 在定义域 X 上，对域内的点 x∗ ，如果存在某个 ϵ>0 使得距离 x∗ 小于 ϵ 的邻域范围内的所有点 x 都满足 f（x∗）≤f（x） ，则点 x∗ 被认为是局部极小值点。如下图所示：

然而，全局极小值在函数定义域的范围内都成立。

给定函数 f 在定义域 X 上，如果点 x∗ 是全局最小值点，那么 f（x∗）≤f（x） 对所有定义域上的点 x∗ 均成立。

所以以上我们所有的工作只是找到了一个局部最小值点，但在现实生活中，我们经常想要找到全局最小值点…

4.5 如何找到全局最小值点？

有一个简单的方法来找到全局最小值点：

1. 找到所有局部极小值点
2. 找到所有局部极小值点中最小的一个，这就是全局最小值点。

另一种方法是研究我们试图最小化的函数，如果这个函数是凸的，那么我们确定它的局部极小值就是全局最小值。

5. 结论

我们发现，找到函数的最小值并不是那么简单，甚至有时找到的不是全局最小值。但是，一些称为凸函数的函数却很容易求得全局最小值。什么是凸函数？继续阅读本教程系列的第5部分就可以找到答案了！谢谢阅读。