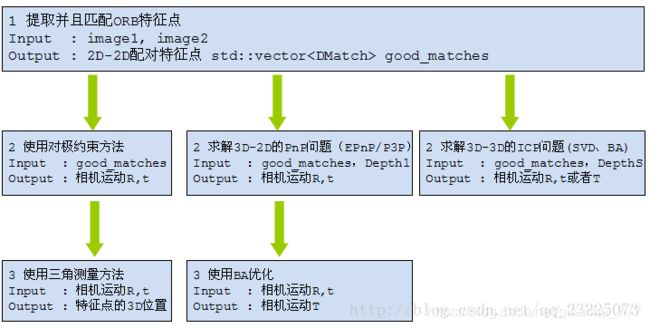
视觉SLAM十四讲-第七讲笔记
主要内容
本章开始进入视觉里程计(VO)部分,VO按是否需要提取特征,分为特征点法的前端和不提特征的前端。这一章讲的是基于特征点法的前端,分为以下内容。
- 特征点法:找到两张2D图像上的匹配点。
- 对极几何:根据2D-2D特征点对求解R,t。
- 三角测量:根据2D-2D特征点求深度。
- PnP:根据3D点云和匹配的2D图像求R,t。
- ICP:求两个点云之间的R,t。
关系是:
- 特征点法找到2D图像的匹配点对,用于对极几何和pnp
- 对极几何求出2D-2D的位姿。
- 根据对极几何求出的位姿,三角测量求出2D-2D的深度。
- 根据三角测量求出的深度,可以初始化单目SLAM,得到三维点信息;或用RGBD相机获得三维信息。知道3D信息,对于下一张2D图像,可根据特征点法找到的匹配点对,使用PNP,求出位姿信息和深度信息。
- 根据pnp求出的深度信息;或直接用RGBD得到的两个点云,可以用ICP,求出两个点云之间的位姿变换。
一、特征点法
这部分内容,讲述了提取2D图像的特征点,并对不同图像之间的特征点进行匹配,得到匹配的特征点对。这些匹配点是后面用来估计相机位姿的基础。
特征点:在SLAM中被成为路标。分为关键点和描述子。
对于SLAM来说,SIFT太慢,FAST没有方向信息,使用改进FAST的ORB特征。
ORB特征
关键点:Oriented FAST
是改进的,具有方向性的FAST描述子。
FAST用于检测局部像素灰度明显变化的位置,思想是看邻域内有没有连续N个和它差T灰度的点。加上NMS和其他遍历的加速trick。
ORB的改进:
- 根据FAST关键点的Harris响应值,选取前N大的,以固定特征点数目。
- 构建图像金字塔,解决尺度问题。
- 使用灰度质心法,解决旋转问题。(加一个几何中心到质心的向量)
描述子:BRIEF
是一种二进制描述子,描述了关键点附近两个像素的大小关系。
特征匹配
局部特征会导致误匹配,难以解决。
BRIEF描述子使用汉明距离进行相似性度量,快速近似最近邻(FLANN)适合数目多的特征点匹配。
二、对极几何
- 已知:匹配点对 p 1 p_1 p1, p 2 p_2 p2的像素坐标。
- 给定:两张二维图像,二维图像上特征点的匹配关系。
- 未知:P的三维空间坐标, I 1 I_1 I1到 I 2 I_2 I2的变换矩阵( T 1 , 2 T_{1,2} T1,2,即 R , t R,t R,t)。
一般是用于__单目SLAM的初始化__,用对极几何可求出位姿,在用三角测量估计三维空间点的位置后,就能用其他更准确的方法继续求解了。
1. 对极约束
设P在图1的相机坐标系下,坐标为:
P = [ X , Y , Z ] T P=[X,Y,Z]^T P=[X,Y,Z]T
p 1 p_1 p1, p 2 p_2 p2的像素坐标(单位像素):
s 1 p 1 = K P , s 2 p 2 = K ( R P + t ) s_1p_1=KP, s_2p_2=K(RP+t) s1p1=KP,s2p2=K(RP+t)
其归一化平面坐标(单位米):
x 1 = K − 1 p 1 , x 2 = K − 1 p 2 x_1=K^{-1}p_1,x_2=K^{-1}p_2 x1=K−1p1,x2=K−1p2
得到:
x 2 = R x 1 + t x_2=Rx_1+t x2=Rx1+t
这里的 x x x是齐次坐标,等式表达了一个齐次关系。
两边同时左乘 t ‘ {t‘} t‘,这个东西相当于与它做外积,得到的结果和它、 x 2 x_2 x2都垂直。因此再左乘一个 x 2 T x_2^T x2T,就得到了0。
最终得到:
x 2 T t ’ R x 1 = 0 x_2^Tt’Rx_1=0 x2Tt’Rx1=0
中间部分写成 E E E矩阵,称为本质矩阵:
x 2 T E x 1 = 0 x_2^TEx_1=0 x2TEx1=0
带入 p 1 p_1 p1, p 2 p_2 p2:
p 2 K − T t ’ R K − 1 p 1 = 0 , E = t ‘ R p_2K^{-T}t ’RK^{-1}p_1=0,E=t^{‘}R p2K−Tt’RK−1p1=0,E=t‘R
中间写成 F F F矩阵,称为基础矩阵:
p 2 F p 1 = 0 , F = K − T t R K − 1 p_2Fp_1=0,F=K^{-T}tRK^{-1} p2Fp1=0,F=K−TtRK−1
t’是t的反对称矩阵。
这两个式子称为对极约束。根据对极约束,估计 R , t R,t R,t的方法为:
- 根据匹配点的位置,求出 E E E或者 F F F。
- 根据 E E E或者 F F F,求出 R , t R,t R,t。
2. 求解本质矩阵E
本质矩阵长什么样子:
- 大小为3x3
- 由平移和旋转定义,共有3+3=6个自由度
- 因为对极约束,E具有尺度等价性,自由度-1,共五个。
八点法
根据对极约束,最少五对点就能求出来E,为了方便,一般使用八对点。
写出由八对点构成的线性方程组,可以解出来E。
估计相机运动
对E做SVD,就能求出来 R , t R,t R,t。可以得到四组解(深度正/负,相机位置的左/右):
![]()
因为深度要是正的才合法,可以把解带入一个点看看深度是否都为正(用三角测量?),从中选出最终解。
3. 单应矩阵
描述了两个平面之间的映射关系。
单应矩阵:H。自由度为8,可通过四对匹配特征点算出。
单应性:当特征点共面,或发生纯旋转时,自由度下降。
4. 单目SLAM的一些问题
尺度不确定性
t的尺度不确定性。对t乘任意倍数,对极约束依然成立。
单目SLAM的初始化:对t进行归一化,固定尺度,或吃实话时,所有特征点的平均深度为1。
纯旋转问题
若是纯旋转,t为0,则E为0,无法求解R。
单目初始化不能只有旋转,必须要有平移。
多于八对点
计算最小二乘解。
或使用RANSAC,来避免误匹配的影响。
5. 三角测量
单目SLAM(2d-2d)中,使用对极约束估计 R , t R,t R,t,使用三角测量估计深度。
三、3D-2D PnP
- 给定:一张已知特征点3D位置的图像,一张二维图像。
- 已知:特征点在世界坐标系(指的是相机最初位置的那个坐标系)下的三维坐标,特征点映射到图像上的二维坐标,三维- - 坐标系中的特征点与二维图像上点的匹配关系。
- 未知:相机坐标系在世界坐标系下的位姿,特征点在相机坐标系下的深度。
- 最初使用对极几何,初始化出特征点的深度。对于后续的二维图像(当前帧),当前帧与之前帧进行特征点匹配,匹配到的点若之前已经估计出深度,就知道了世界坐标系下的三维坐标和当前帧二维点的匹配关系,可以用PNP求解当前帧的相机,相对于世界坐标系的位姿变换。
1. 直接线性变换
用来求 R , t R,t R,t。
待求变量 R , t R,t R,t写成增广矩阵,共有3*4=12个未知量。
变换可得,一对匹配点能够写成两个等式,最少通过6对匹配点,可以求出 R , t R,t R,t。匹配点大于六对时,可以用SVD等方法求最小二乘解。
要注意使得求得的旋转矩阵满足约束。
2 . P3P
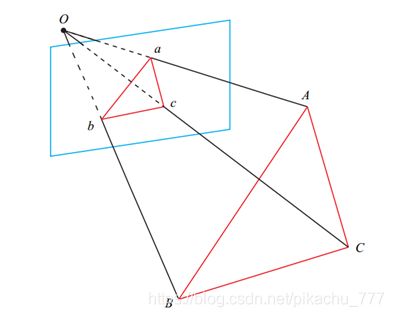
**用来求三维点在相机坐标系下的深度。**得到深度后,再用ICP求位姿变换。
仅用三对匹配点,和一个验证点。
已知 A , B , C A,B,C A,B,C在世界坐标系下的三维点坐标, a , b , c a,b,c a,b,c是其在像平面的投影,已知其归一化坐标。
未知 A , B , C A,B,C A,B,C在相机坐标系下的坐标。
根据三角形的相似关系和余弦定理,可以推出:
O A 2 + O B 2 − 2 O A O B c o s < a , b > = A B 2 OA^2+OB^2-2OAOBcos<a,b>=AB^2 OA2+OB2−2OAOBcos<a,b>=AB2
O B 2 + O C 2 − 2 O B O C c o s < b , c > = B C 2 OB^2+OC^2-2OBOCcos<b,c>=BC^2 OB2+OC2−2OBOCcos<b,c>=BC2
O A 2 + O C 2 − 2 O A O C c o s < a , c > = A C 2 OA^2+OC^2-2OAOCcos<a,c>=AC^2 OA2+OC2−2OAOCcos<a,c>=AC2
记 x = O A / O C x=OA/OC x=OA/OC, y = O B / O C y=OB/OC y=OB/OC,得:
x 2 + y 2 − 2 x y c o s < a , b > = A B 2 / O C 2 x^2+y^2-2xycos<a,b>=AB^2/OC^2 x2+y2−2xycos<a,b>=AB2/OC2
Y 2 + 1 − 2 y c o s < b , c > = B C 2 / O C 2 Y^2+1-2ycos<b,c>=BC^2/OC^2 Y2+1−2ycos<b,c>=BC2/OC2
x 2 + 1 − 2 x c o s < b , c > = A C 2 / O C 2 x^2+1-2xcos<b,c>=AC^2/OC^2 x2+1−2xcos<b,c>=AC2/OC2
记 v = A B 2 / O C 2 , U V = B C 2 / O C 2 , w v = A C 2 / O C 2 v=AB^2/OC^2,UV=BC^2/OC^2,wv=AC^2/OC^2 v=AB2/OC2,UV=BC2/OC2,wv=AC2/OC2,得:
( 1 − u ) y 2 − u x 2 − c o s < b , c > y + 2 u x y c o s < a , b > + 1 = 0 (1-u)y^2-ux^2-cos<b,c>y+2uxycos<a,b>+1=0 (1−u)y2−ux2−cos<b,c>y+2uxycos<a,b>+1=0
( 1 − w ) x 2 − w y 2 − c o s < a , c > y + 2 w x y c o s < a , b > + 1 = 0 (1-w)x^2-wy^2-cos<a,c>y+2wxycos<a,b>+1=0 (1−w)x2−wy2−cos<a,c>y+2wxycos<a,b>+1=0
其中 x , y x,y x,y未知,也就是 A , B , C A,B,C A,B,C在相机坐标系下的坐标 O A , O B , O C OA,OB,OC OA,OB,OC的长度未知。
方程最多得到四个解,用验证点来计算最可能的解,得到3D坐标。之后可以求解两组3D坐标之间的 R , t R,t R,t。
存在问题:
- 只利用三个点的信息,多于三组点时,难以利用。
- 存在误匹配或噪声,则失效。
3. bundle adjustment
从非线性优化的角度,一起求解点的深度和相机位姿。
可以用它对PnP和ICP的结果进行优化。
使用李代数表示相机姿态:
s i u i = K e x p ( ϵ ) ^ P i s_iu_i=Kexp(\epsilon\hat)P_i siui=Kexp(ϵ)^Pi
其中, P i P_i Pi是三维空间点坐标, u i u_i ui是像素坐标。
等式中存在误差:
- e x p ( ϵ ) ^ exp(\epsilon\hat) exp(ϵ)^的估计误差。
- u i u_i ui观测噪声。
定义误差:
e i = u i − 1 / s i K e x p ( ϵ ) ^ P i e_i=u_i-1/s_iKexp(\epsilon\hat)P_i ei=ui−1/siKexp(ϵ)^Pi
最小化重投影误差:上式定义的误差,是观测值,与估计的位姿把三维点重新投影到像平面上的误差。
ϵ ∗ = a r g m i n 1 2 ∑ i = 1 n ∣ ∣ u i − 1 / s i K e x p ( ϵ ) ^ P i ∣ ∣ 2 2 \epsilon^*=argmin \frac{1}{2}\sum^n_{i=1}||u_i-1/s_iKexp(\epsilon\hat)P_i||^2_2 ϵ∗=argmin21i=1∑n∣∣ui−1/siKexp(ϵ)^Pi∣∣22
最小二乘问题:
- 变量:位姿的李代数表示: ϵ \epsilon ϵ。
- 目标:最小化重投影误差,求最优的位姿和空间点位姿。
- 方法:求e关于 ϵ \epsilon ϵ或 P P P的导数,进行非线性优化。
问题转变成如何求导(J矩阵):
e ( x + δ x ) ≈ e ( x ) + J δ x e(x+\delta x)≈e(x)+J\delta x e(x+δx)≈e(x)+Jδx
x x x为 ϵ \epsilon ϵ或 P P P。
求最优位姿
定义P在相机坐标系下的坐标为 P ′ = e x p ( ϵ ) ^ P P'=exp(\epsilon\hat)P P′=exp(ϵ)^P。使用链式法则:
∂ e ∂ ϵ = ∂ e ∂ P ′ ∂ P ′ ∂ ϵ \frac{\partial e}{\partial \epsilon} = \frac{\partial e}{\partial P'}\frac{\partial P'}{\partial \epsilon} ∂ϵ∂e=∂P′∂e∂ϵ∂P′
第一项是2x3的矩阵,第二项是3x6的矩阵,最终J为2x6.
求最优深度
关于 P P P求导。利用链式法则:
∂ e ∂ P = ∂ e ∂ P ′ ∂ P ′ ∂ P \frac{\partial e}{\partial P} = \frac{\partial e}{\partial P'}\frac{\partial P'}{\partial P} ∂P∂e=∂P′∂e∂P∂P′
四、3D-3D ICP
- 已知:两组三维点坐标。(可以是对于同一组特征点,不同相机坐标系下的坐标,也可以是同一相机,拍摄不同位置的空间坐标?)
- 未知:两个相机坐标系之间的位姿转换。
- 目标:求变换矩阵,使得匹配点之间的累积距离最小。 p i = R P i ′ + t pi=RP'_i+t pi=RPi′+t
### 1. SVD方法
误差:
e i = p i − ( R P i ′ + t ) e_i=pi-(RP'_i+t) ei=pi−(RPi′+t)
求使 ∑ i e i \sum_i e_i ∑iei最小的 R , t R,t R,t。
最终目标函数可化简为:
m i n R , t J = 1 2 ∑ i ∣ ∣ p i − p − R ( p i ′ − p ′ ) ∣ ∣ 2 2 + ∣ ∣ p − R p ′ − t ∣ ∣ 2 min_{R,t}J=\frac{1}{2} \sum_i ||p_i-p-R(p_i'-p')||^2_2+||p-Rp'-t||^2 minR,tJ=21i∑∣∣pi−p−R(pi′−p′)∣∣22+∣∣p−Rp′−t∣∣2
先优化第一项,求得使第一项最小的 R R R。
再优化第二项,第二项是平方项,最小为0,即在 R R R的基础上,求使第二项为0的 t t t。
其中 p , p ′ p,p' p,p′是两组点的质心。
2. 非线性优化方法
也是用李代数表达位姿,然后对李代数求导。
ICP问题只有唯一解或无穷多解,在唯一解时,极小值就是全局最优值,即可以任意选择初值。