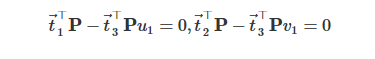《视觉SLAM十四讲精品总结》7:VO—— 3D-2D:PnP+BA
引出:
2D-2D的对极几何需要8个以上点对,且存在初始化、纯旋转和尺度问题。
特征点3D位置可以由三角化或RGB-D相机深度图确定。
因此,双目或RGB-D相机直接使用PnP估计相机运动。单目视觉里程计,首先初始化,然后才能PnP。
PnP为( Perspective-n-Point)的简称,即给出n个3D空间点及其投影位置时,如何求解相机的位姿R t。
PnP优点:不需要对极约束,3个的匹配点对就可以运动估计。
内容:
直接线性变换(DLT)
P3P及实现
BA(Bundle Adjustment)及实现
一、DLT
- 每个特征点对提供两个关于t的线性约束,t 一共12维,至少需要6个特征点对实现T的线性求解。
- 匹配点数大于6,SVD最小二乘解。
- 缺点:T矩阵看成12个未知数,忽略了他们之间的联系。
二、P3P
1、原理:利用了三角形相似,求解投影点abc在相机坐标系下的3D坐标,然后将问题转为3D-3D问题。
在SLAM实用:先P3P估计相机位姿R t, 之后构建最小二乘优化问题对估计值进行调整。
2、代码实现
调用solvePnP函数
bool cv::solvePnP(objectPoints,imagePoints,cameraMatrix,distCoeffs,
OutputArray r, OutputArray t,
bool useExtrinsicGuess = false,int flags = SOLVEPNP_ITERATIVE ) | objectPoints | Array of object points in the 世界坐标系, Nx3 1-channel or 1xN/Nx1 3-channel, where N is the number of points. vector |
| imagePoints | Array of corresponding 第二张图的像素坐标, Nx2 1-channel or 1xN/Nx1 2-channel, where N is the number of points. vector |
| cameraMatrix | Input camera matrix K |
| distCoeffs | Input vector of distortion coefficients (k1,k2,p1,p2[,k3[,k4,k5,k6[,s1,s2,s3,s4[,τx,τy]]]]) of 4, 5, 8, 12 or 14 elements. If the vector is NULL/empty, the zero distortion coefficients are assumed. |
| rvec | Output 旋转向量 (see Rodrigues ) that, together with tvec , brings points from the model coordinate system to the camera coordinate system.需要罗德里格斯公式化为旋转矩阵 |
| tvec | Output translation vector. |
| useExtrinsicGuess | Parameter used for SOLVEPNP_ITERATIVE. If true (1), the function uses the provided rvec and tvec values as initial approximations of the rotation and translation vectors, respectively, and further optimizes them |
- 缺点:P3P只利用了3个点信息
- 如果3D或2D点受到噪声影响,或者误匹配,算法失效。
主框架
#include
#include
#include
using namespace std;
using namespace cv;
void find_feature_matches(
const Mat& img_1, const Mat& img_2,
std::vector& keypoints_1,
std::vector& keypoints_2,
std::vector< DMatch >& matches);
Point2d pixel2cam(const Point2d& p, const Mat& K);
void bundleAdjustment(
const vector points_3d,
const vector points_2d,
const Mat& K,
Mat& R, Mat& t
);
int main()
{
Mat img1 = imread("1.png");
Mat img2 = imread("2.png");
Mat d1 = imread("1_depth.png"); // 深度图为16位无符号数,单通道图像
//1. 找到特征点和匹配关系
vector keypoint1, keypoint2;
vector matches;
find_feature_matches(img1,img2,keypoint1,keypoint2,matches);
Mat K = (Mat_(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
//2. 第一张图像给出3D坐标,第二张给像素2d坐标
vector pts_3d;
vector pts_2d;
for (DMatch m : matches)
{
//3. 3D坐标由第一张的像素坐标转为相机坐标,再乘上深度,为世界坐标
ushort d = d1.ptr (int(keypoint1[m.queryIdx].pt.y))[int (keypoint1[m.queryIdx].pt.x)];
d = d / 1000;
Point2d p1 = pixel2cam(keypoint1[m.queryIdx].pt, K);
Point3f p2(p1.x*d, p1.y*d, d);
pts_3d.push_back(p2);
pts_2d.push_back(keypoint2[m.trainIdx].pt);
cout << "3d-2d pairs" << pts_3d.size() << endl;
//4. 调用函数p3p,求解r,t
Mat R,r, t;
solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false, SOLVEPNP_EPNP);
Rodrigues(r, R);
}
}
- 注解:
Mat d1 = imread("1_depth.png"); ushort d = d1.ptr(int(keypoint1[m.queryIdx].pt.y))[int(keypoint1[m.queryIdx].pt.x)]; d1是深度图,Mat类型的ptr是指针,获得像素点深度,首先得到行地址,之后列指针 (pt.y)[pt.x]
-
第一张图像给出3D坐标,第二张给像素2d坐标; 其中3D坐标由第一张的像素坐标转为相机坐标,再乘上深度,为世界坐标。
-
Rodrigues(r, R);solvepnp得到的是旋转向量r,需要通过罗德里格斯公式换为旋转矩阵R。即李代数向李群的转换。
三、BA
这种优化方法用在SLAM上时称为集束调整(Bundle Adjustment,BA)。
“集束调整”名称的含义是说,通过调整相机的姿态使3D路标点发出的光线都能汇聚到相机的光心。
回顾g2o图优化库,优化变量作为顶点,误差项作为变,构造一个图。
本节,顶点是3D坐标(XYZ)和相机位姿R t,误差项是重投影误差。把问题建模成一个最小二乘的图优化问题。
void bundleAdjustment (
const vector< Point3f > points_3d,
const vector< Point2f > points_2d,
const Mat& K,
Mat& R, Mat& t )
{
// 1. 初始化g2o,设定线性方程求解器Blocksolver和迭代算法
typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block; // pose维度为 6, 观测landmark维度为 3
Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse();
Block* solver_ptr = new Block ( linearSolver );
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
//图优化,设置求解器
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm ( solver );
// 2.1 图中增加顶点位姿pose
g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // 相机的李代数位姿,VertexSE3Expmap类
Eigen::Matrix3d R_mat;
R_mat <<
R.at ( 0,0 ), R.at ( 0,1 ), R.at ( 0,2 ),
R.at ( 1,0 ), R.at ( 1,1 ), R.at ( 1,2 ),
R.at ( 2,0 ), R.at ( 2,1 ), R.at ( 2,2 );
pose->setId ( 0 );
//相机位姿类型SE3Quat,四元数+位移向量
pose->setEstimate ( g2o::SE3Quat (
R_mat,
Eigen::Vector3d ( t.at ( 0,0 ), t.at ( 1,0 ), t.at ( 2,0 ) )
) );
optimizer.addVertex ( pose );
// 2.2 图中增加顶点坐标point
int index = 1;
for ( const Point3f p:points_3d )
{
g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();//空间点位置类型,VertexSBAPointXYZ
point->setId ( index++ );
point->setEstimate ( Eigen::Vector3d ( p.x, p.y, p.z ) );
point->setMarginalized ( true ); // g2o 中必须设置 marg 参见第十讲内容
optimizer.addVertex ( point );
}
// 相机内参K,CameraParameters类
g2o::CameraParameters* camera = new g2o::CameraParameters (
K.at ( 0,0 ), Eigen::Vector2d ( K.at ( 0,2 ), K.at ( 1,2 ) ), 0
);
camera->setId ( 0 );
optimizer.addParameter ( camera );
// 3. 图中增加边
index = 1;
for ( const Point2f p:points_2d )
{
g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();//投影方程边类型EdgeProjectXYZ2UV
edge->setId ( index );
edge->setVertex ( 0, dynamic_cast ( optimizer.vertex ( index ) ) );
edge->setVertex ( 1, pose );
edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
edge->setParameterId ( 0,0 );
edge->setInformation ( Eigen::Matrix2d::Identity() );
optimizer.addEdge ( edge );
index++;
}
//4. 执行优化
optimizer.initializeOptimization();
optimizer.optimize ( 100 );
cout<//继承了 BaseVertex <6, SE3Quat> 6维李代数,相机位姿SE3Quat李代数
class G2O_TYPES_SBA_API VertexSE3Expmap : public BaseVertex<6, SE3Quat>{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
//1. 默认构造函数
VertexSE3Expmap();
//2. 重置函数
virtual void setToOriginImpl() {
_estimate = SE3Quat();
}
//3. 更新函数
virtual void oplusImpl(const double* update_) {
//成员函数Map映射成6维向量
Eigen::Map update(update_);
//李代数上增量左乘
setEstimate(SE3Quat::exp(update)*estimate());
}
//4. 存盘和读盘:留空
bool read(std::istream& is);
bool write(std::ostream& os) const;
}; EdgeProjectXYZ2UV::computeError()
//继承了BaseBinaryEdge类,观测值是2维,类型Vector2D,
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV : public BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
//1. 默认初始化
EdgeProjectXYZ2UV();
//2. 计算误差
void computeError() {
//李代数相机位姿v1
const VertexSE3Expmap* v1 = static_cast(_vertices[1]);
// 顶点v2
const VertexSBAPointXYZ* v2 = static_cast(_vertices[0]);
//相机参数
const CameraParameters * cam
= static_cast(parameter(0));
//误差计算,测量值减去估计值,也就是重投影误差obs-cam
//估计值计算方法是T*p,得到相机坐标系下坐标,然后在利用camera2pixel()函数得到像素坐标。
Vector2D obs(_measurement);
_error = obs-cam->cam_map(v1->estimate().map(v2->estimate()));
}
//3. 线性增量函数,也就是雅克比矩阵J的计算方法
virtual void linearizeOplus();
//4. 相机参数
CameraParameters * _cam;
bool read(std::istream& is);
bool write(std::ostream& os) const;
}; - .map映射
_error = _measurement - camera_->camera2pixel(pose->estimate().map(point_) );里面有个map()函数。看一下这个函数的源码:
Vector3D map(const Vector3D & xyz) const
{
return _r*xyz + _t;
} 传入一个3D点,返回r*p+t,很明显就是求变换后点的坐标。
在g2o中,用SE3Quat类型表示变换T,此类型中有个成员函数就是map(),作用为对一个3D点进行坐标变换,
EdgeProjectXYZ2UV::linearizeOplus()
void EdgeProjectXYZ2UVPoseOnly::linearizeOplus()
{
/**
* 这里说一下整体思路:
* 重投影误差的雅克比矩阵在书中P164页式7.45已经呈现,所以这里就是直接构造,
* 构造时发现需要变换后的空间点坐标,所以需要先求出。
*/
//1. 首先还是从顶点取出位姿
g2o::VertexSE3Expmap* pose = static_cast ( _vertices[1] );
//2. 这由位姿构造一个四元数形式T
g2o::SE3Quat T ( pose->estimate() );
//3. 用T求得变换后的3D点坐标。T.map(p)就是T*p
g2o::VertexSBAPointXYZ* point_ = static_cast(_vertices[0]);
Vector3d xyz_trans = T.map ( point_ );
//OK,到这步,变换后的3D点xyz坐标就分别求出来了,后面的z平方,纯粹是为了后面构造J时方便定义的,因为需要多处用到
double x = xyz_trans[0];
double y = xyz_trans[1];
double z = xyz_trans[2];
double z_2 = z*z;
//4. 相机参数
const CameraParameters* cam=static_cast(parameter(0));
//4. 直接各个元素构造J就好了,对照式7.45是一模一样的,2*6的矩阵。
_jacobianOplusXi ( 0,0 ) = x*y/z_2 *camera_->fx_;
_jacobianOplusXi ( 0,1 ) = - ( 1+ ( x*x/z_2 ) ) *camera_->fx_;
_jacobianOplusXi ( 0,2 ) = y/z * camera_->fx_;
_jacobianOplusXi ( 0,3 ) = -1./z * camera_->fx_;
_jacobianOplusXi ( 0,4 ) = 0;
_jacobianOplusXi ( 0,5 ) = x/z_2 * camera_->fx_;
_jacobianOplusXi ( 1,0 ) = ( 1+y*y/z_2 ) *camera_->fy_;
_jacobianOplusXi ( 1,1 ) = -x*y/z_2 *camera_->fy_;
_jacobianOplusXi ( 1,2 ) = -x/z *camera_->fy_;
_jacobianOplusXi ( 1,3 ) = 0;
_jacobianOplusXi ( 1,4 ) = -1./z *camera_->fy_;
_jacobianOplusXi ( 1,5 ) = y/z_2 *camera_->fy_;
}
}
注意:
1、相机位姿顶点类VertexSE3Expmap使用了李代数表示相机位姿,而不是使用旋转矩阵和平移矩阵。
这是因为旋转矩阵是有约束的矩阵,它必须是正交矩阵且行列式为1。使用它作为优化变量就会引入额外的约束条件,从而增大优化的复杂度。而将旋转矩阵通过李群-李代数之间的转换关系转换为李代数表示,就可以把位姿估计变成无约束的优化问题,求解难度降低。
2、在重投影误差边类EdgeProjectXYZ2UV中,已经为相机位姿和3D点坐标推导了雅克比矩阵,以计算迭代的增量方向。