查找算法

##查找算法

引言

常见的七种查找算法有：顺序查找、二分查找、插值查找、斐波那契查找、树表查找、分块查找、哈希查找。其中二分查找、插值查找、斐波那契查找可以归为一类——插值查找，插值查找、斐波那契查找是在二分查找的基础上经过优化的查找算法。

###定义

查找是在大量的信息中寻找一个特定的信息元素，用关键字标识一个数据元素，查找时根据给定的某个值，在表中确定一个关键字的值等于给定值的记录或数据元素。

分类

1. 静态查找和动态查找

   注：静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。

2. 无序查找和有序查找。

   无序查找：被查找数列有序无序均可；
   有序查找：被查找数列必须为有序数列。

注：平均查找长度（Average Search Length，ASL）：需和指定key进行比较的关键字的个数的期望值，称为查找算法在查找成功时的平均查找长度。
　　对于含有n个数据元素的查找表，查找成功的平均查找长度为：ASL = Pi*Ci的和。
　　Pi：查找表中第i个数据元素的概率。
Ci : 找到第i个数据元素时已经比较过的次数。

顺序查找

• 说明：顺序查找适用于存储结构为顺序存储或链接存储的线性表。

• 基本思想：顺序查找也称为线形查找，属于无序查找算法。从数据结构线形表的一端开始，顺序扫描，依次将扫描到的结点关键字与给定值k相比较，若相等则表示查找成功；若扫描结束仍没有找到关键字等于k的结点，表示查找失败。

• 复杂度分析：查找成功时的平均查找长度为：（假设每个数据元素的概率相等） ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
  　　当查找不成功时，需要n+1次比较，时间复杂度为O(n);
  　　所以，顺序查找的时间复杂度为O(n)。

• 优点：算法简单，对表的结果无任何要求，无论是用向量还是用链表来存放结点，也无论结点之间是否按关键字有序，它都同样适用。

• 缺点： 查找效率低，因此，当n较大时不宜采用顺序查找。

  public static int seqSearch(int[] arrs,int num){
  //        无序查找
          for (int i = 0;i<arrs.length;i++){
              if (arrs[i] == num){
                  return i;
              }
          }
          return -1;
  //        有序查找
          for (int i = 0;i<arrs.length;i++){
              if (arrs[i] == num){
                  return i;
              }else if (arrs[i] > num){
                  break;
              }
              System.out.println(arrs[i]);
          }
          return -1;
      }
  

###二分查找

• 说明：元素必须是有序的，如果是无序的则要先进行排序操作。

• 基本思想：也称为是折半查找，属于有序查找算法。用给定值k先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。

• 复杂度分析：最坏情况下，关键词比较次数为log2(n+1)，且期望时间复杂度为O(log2n)；

• 优点：比较次数少，查找速度快，平均性能好

• 缺点：待查表为有序数组，插入删除困难

• 注：折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。

  //    二分查找非递归算法
      public static int binarySearch(int[] arr,int key){
  //        最小范围下标
          int minIndex = 0;
  //        最大范围下标
          int maxIndex = arr.length-1;
  //        中间范围下标
          int midIndex = (minIndex+maxIndex)/2;
          while (minIndex <= maxIndex){
  //            判断要查找的key与中间下标值的大小关系
              if (arr[midIndex] > key){
  //                中间下标数据值大于key
                  maxIndex = midIndex - 1;
              }else if (arr[midIndex] < key){
  //                中间下标数据值小于key
                  minIndex = midIndex + 1;
              }else{
  //                找到该数据，结束查找
                  return midIndex;
  
              }
  //            当边界发生变化时，需要更新中间下标
              midIndex = (minIndex+maxIndex)/2;
          }
          return -1;
      }
  //    二分查找递归算法
      public static int search2(int key,int[] arr,int minIndex,int maxIndex) {
          if(minIndex > maxIndex){
              return -1;
          }
          int midIndex = (minIndex + maxIndex)/2;
          if(key<arr[midIndex]){
              return search2(key,arr,minIndex,midIndex-1);
          }else if(key>arr[midIndex]){
              return search2(key,arr,midIndex+1,maxIndex);
          }else{
              return midIndex;
          }
      }
  

###插值查找

• 说明：插值查找与二分查找一样，只适用于有序表的查找。插值查找是在二分查找的基础上做了一些优化的查找算法

• 在进行二分查找时，我们一开始是选择了从查找表的中间开始查找，而在实际应用中，比如说在英文字典里面查“apple”，你下意识翻开字典是翻前面的书页还是后面的书页呢？如果再让你查“zoo”，你又怎么查？很显然，这里你绝对不会是从中间开始查起，而是有一定目的的往前或往后翻。

• 折半查找这种查找方式，不是自适应的，因此我们可以对二分查找进行一些优化：

  二分查找中的查找点为：

  ​ midIndex = (minIndex+maxIndex)/2；

  通过类比，我们可以将查找的点改进为如下：

  ​ midIndex=minIndex+(key-arr[minIndex])/(arr[maxIndex]-arr[minIndex])*(maxIndex -minIndex)；

  也就是将上述的比例参数1/2改进为自适应的，根据关键字在整个有序表中所处的位置，让mid值的变化更靠近关键字key，这样也就间接地减少了比较次数。

  基本思想：基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，差值查找也属于有序查找。

  注：对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

  //    插值查找
      public static int interpolationLookup(int[] arr,int key){
  //        最小范围下标
          int minIndex = 0;
  //        最大范围下标
          int maxIndex = arr.length-1;
  //        中间范围下标
          int midIndex = minIndex+(key-arr[minIndex])/(arr[maxIndex]-arr[minIndex])*(minIndex+maxIndex);
          while (minIndex <= maxIndex){
  //            判断要查找的key与中间下标值的大小关系
              if (arr[midIndex] > key){
  //                中间下标数据值大于key
                  maxIndex = midIndex - 1;
              }else if (arr[midIndex] < key){
  //                中间下标数据值小于key
                  minIndex = midIndex + 1;
              }else{
  //                找到该数据，结束查找
                  return midIndex;
  
              }
  //            当边界发生变化时，需要更新中间下标
              midIndex = minIndex+(key-arr[minIndex])/(arr[maxIndex]-arr[minIndex])*(minIndex+maxIndex);
          }
          return -1;
      }
  

斐波那契查找

• 斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（从第三个数开始，后边每一个数都是前两个数的和）。然后我们会发现，随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性，我们就可以将黄金比例运用到查找技术中。

• 黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。

• 

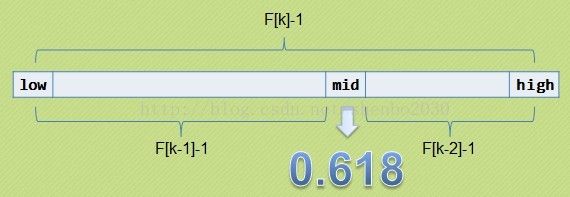
• 说明：斐波那契查找也是插值查找的一种，它每次的查找点都是未查找部分的黄金分割点，可以提高查找效率，同时，它也属于一种有序查找算法。

• 斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。

  开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种

  1）相等，mid位置的元素即为所求

  2）>，low=mid+1,k-=2;

  说明：low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个。

  3）<，high=mid-1,k-=1。

  说明：low=mid+1说明待查找的元素在[low,mid-1]范围内，k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个。

  //    斐波那契查找
      public static int fibonacciLookup(int[] arr,int key){
  //        初始化一个斐波那契数列
          ArrayList<Integer> fib = new ArrayList<>();
          fib.add(1);
          int i =1;
          while (arr.length > fib.get(i-1)) {
              if (i < 2){
                  fib.add(1);
              }else {
                  int result = fib.get(i-1)+fib.get(i-2);
                  fib.add(result);
              }
              i++;
          }
  //        查找过程
          int minIndex = 0;
          int maxIndex = arr.length-1;
  //        第一个黄金分割点
          int k = fib.size()-2;
          int midIndex;
          int index;
          while (minIndex <= maxIndex) {
              if (k >= 0){
                  midIndex = minIndex+fib.get(k)-1;
              }else {
                  break;
              }
              index = midIndex>=arr.length?arr.length-1:midIndex;
  //            判断要查找的key与中间下标值的大小关系
              if (arr[index] > key) {
  //                中间下标数据值大于key
                  maxIndex = midIndex - 1;
                  k -= 1;
              } else if (arr[index] < key) {
  //                中间下标数据值小于key
                  minIndex = index + 1;
                  k -= 2;
              } else {
  //                找到该数据，结束查找
                  if (midIndex<arr.length){
                      return midIndex;
                  }else {
                      return arr.length-1;
                  }
              }
          }
          return -1;
      }
  

树表查找

• 最简单的树表查找算法——二叉树查找算法。

  基本思想：二叉查找树是先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后在就行和每个节点的父节点比较大小，查找最适合的范围。 这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。

  二叉查找树（BinarySearch Tree，也叫二叉搜索树，或称二叉排序树Binary Sort Tree）或者是一棵空树，或者是具有下列性质的二叉树：

  1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

  2）若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

  3）任意节点的左、右子树也分别为二叉查找树。

  二叉查找树性质：对二叉查找树进行中序遍历，即可得到有序的数列。

• 基于二叉查找树进行优化，进而可以得到其他的树表查找算法，如平衡树、红黑树等高效算法。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4eR8BpeE-1588753316893)(C:\Users\zl\AppData\Roaming\Typora\typora-user-images\image-20200503145920646.png)]

分块查找

• 分块查找又称索引顺序查找，它是顺序查找的一种改进方法。
  　　算法思想：将n个数据元素"按块有序"划分为m块（m ≤ n）。每一块中的结点不必有序，但块与块之间必须"按块有序"；即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，……
  　　算法流程：
  　　step1 先选取各块中的最大关键字构成一个索引表；
  　　step2 查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；然后，在已确定的块中用顺序法进行查找。

• [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XXg0vzyo-1588753316896)(C:\Users\zl\AppData\Roaming\Typora\typora-user-images\image-20200503153438341.png)]

  /*
  *     索引表类
  * */
  public class IndexItem {
      public int max; //值比较的索引
      public int start; //开始位置
      public int length;//块元素长度(非空)
  
      public IndexItem(int max, int start, int length) {
          this.max = max;
          this.start = start;
          this.length = length;
      }
  }
  /*
  * 分块查找
  * */
  public class Demo3 {
  //    索引表
      static IndexItem[] indexItemList;
  
      public static void main(String[] args) {
          int[] arr = {14,31,8,22,18,43,62,49,35,52,88,78,71,83};
  //        分块
          indexItemList = new IndexItem[]{
                  new IndexItem(31, 0, 5),
                  new IndexItem(62,5,5),
                  new IndexItem(88,10,4)
          };
          System.out.println(blockSearch(arr,49));
      }
      public static int blockSearch(int[] arr,int key){
          IndexItem indexItem = null;
  //        遍历索引表
          for (int i = 0;i<indexItemList.length;i++){
              if (indexItemList[i].max > key){
                 indexItem = indexItemList[i];
                 break;
              }
          }
          if (indexItem == null){
              return -1;
          }
  //        遍历当前块
          for (int i =indexItem.start;i<indexItem.start+indexItem.length;i++){
              if (arr[i] == key){
                  return i;
              }
          }
          return -1;
      }
  }
  

哈希查找

• 什么是哈希表（Hash）？

  我们使用一个下标范围比较大的数组来存储元素。可以设计一个函数（哈希函数， 也叫做散列函数），使得每个元素的关键字都与一个函数值（即数组下标）相对应（即key -> f(key)），于是用这个数组单元来存储这个元素。但是，不能够保证每个元素的关键字与函数值是一一对应的，因此极有可能出现对于不同的元素，却计算出了相同的函数值，这样就产生了"冲突"，换句话说，就是把不同的元素分在了相同的"类"之中。
  　　总的来说，"直接定址"与"解决冲突"是哈希表的两大特点。

• 什么是哈希函数？

  哈希函数的规则是：通过某种转换关系，使关键字适度的分散到指定大小的的顺序结构中，越分散，则以后查找的时间复杂度越小，空间复杂度越高。

  散列因子：（默认为0.75），散列因子越大，查找的时间复杂度越大，散列因子越小，查找的时间复杂度越小。

  算法思想：哈希的思路很简单，如果所有的键都是整数，那么就可以使用一个简单的无序数组来实现：将键作为索引，值即为其对应的值，这样就可以快速访问任意键的值。这是对于简单的键的情况，我们将其扩展到可以处理更加复杂的类型的键。

• 六种哈希函数构造方法：

  1. 直接定值法：

     哈希地址：f(key) = a*key+b (a,b为常数)

     这种方法的优点是：简单，均匀，不会产生冲突。但是需要事先知道 key 的分布情况，适合查找表较小并且连续的情况。

  2. 数字分析法

     比如我们的11位手机号码“136xxxx5889”，其中前三位是接入号，一般对应不同运营公司的子品牌，如130是联通如意通，136是移动神州行等等。中间四位表示归属地。最后四位才是用户号。

     若我们现在要存储某家公司员工登记表，如果用手机号码作为 key，那么极有可能前7位都是相同的，所以我们选择最后四位作为 f(key) 就是不错的选择。

  3. 平方取中法

     故名思义，比如 key 是1234，那么它的平方就是1522756，再抽取中间的3位就是227作为 f(key) 。

  4. 折叠法

     折叠法是将 key 从左到右分割成位数相等的几个部分(最后一部分位数不够可以短些)，然后将这几部分叠加求和，并按哈希表的表长，取后几位作为 f(key) 。

     比如我们的 key 是 9876543210，哈希表的表长为3位，我们将 key 分为4组，987|654|321|0 ，然后将它们叠加求和 987+654+321+0=1962，再取后3位即得到 f(key) = 962 。

  5. 除留余数法

     哈希地址：f(key) = key mod p (p<=m) m为哈希表表长。

  6. 随机数法

     哈希地址：f(key) = random(key)

     这里 random 是随机函数，当 key 的长度不等时，采用这种方法比较合适。

• 解决冲突的方法：

  1. 开放地址法

     开放定址法就是一旦发生了冲突，就去寻找下一个空的哈希地址，只要哈希表足够大，空的哈希地址总是能找到，然后将记录插入。这种方法是最常用的解决冲突的方法。

  2. 链地址法

• 哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制，那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1)；如果没有时间限制，那么我们可以使用无序数组并进行顺序查找，这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。

  /*
       哈希查找
  */
  public class Demo4 {
      // 初始化哈希表
      static int hashLength = 7;
      static int[] hashTable = new int[hashLength];
  
      // 原始数据
      static int[] list = new int[]{13, 29, 27, 28, 26, 30, 38};
  
      public static void main(String[] args){
          // 创建哈希表
          for (int i = 0; i < list.length; i++) {
              insert(hashTable, list[i]);
          }
  
          while (true) {
              // 哈希表查找
              System.out.print("请输入要查找的数据：");
              int result = search(hashTable,22);
              if (result == -1) {
                  System.out.println("对不起，没有找到！");
              } else {
                  System.out.println("数据的位置是：" + result);
              }
          }
      }
  
      /**
       * 方法：哈希表插入
       */
      public static void insert(int[] hashTable, int data) {
          // 哈希函数，除留余数法
          int hashAddress = hash(hashTable, data);
  
          // 如果不为0，则说明发生冲突
          while (hashTable[hashAddress] != 0) {
              // 利用 开放定址法 解决冲突
              hashAddress = (++hashAddress) % hashTable.length;
          }
  
          // 将待插入值存入字典中
          hashTable[hashAddress] = data;
      }
  
      /**
       * 方法：哈希表查找
       */
      public static int search(int[] hashTable, int data) {
          // 哈希函数，除留余数法
          int hashAddress = hash(hashTable, data);
  
          while (hashTable[hashAddress] != data) {
              // 利用 开放定址法 解决冲突
              hashAddress = (++hashAddress) % hashTable.length;
              // 查找到开放单元 或者 循环回到原点，表示查找失败
              if (hashTable[hashAddress] == 0 || hashAddress == hash(hashTable, data)) {
                  return -1;
              }
          }
          // 查找成功，返回下标
          return hashAddress;
      }
  
      /**
       * 方法：构建哈希函数（除留余数法）
       *
       * @param hashTable
       * @param data
       * @return
       */
      public static int hash(int[] hashTable, int data) {
          return data % hashTable.length;
      }
  
  
  }
  

ss] == 0 || hashAddress == hash(hashTable, data)) {
return -1;
}
}
// 查找成功，返回下标
return hashAddress;
}

    /**
     * 方法：构建哈希函数（除留余数法）
     *
     * @param hashTable
     * @param data
     * @return
     */
    public static int hash(int[] hashTable, int data) {
        return data % hashTable.length;
    }


}
```