数据结构与算法——有序向量的二分查找法(C++)
数据结构与算法——有序向量的二分查找法
文章目录
- 数据结构与算法——有序向量的二分查找法
- 1. 程序概览
- 2. 版本A——二分查找 & 斐波拉契查找
- 2.1 二分查找版本A
- 2.2 斐波拉契查找版本A
- 3. 版本B——二分查找
- 4. 版本C——二分查找
- 5. 总结
1. 程序概览
#include 2. 版本A——二分查找 & 斐波拉契查找
2.1 二分查找版本A
- 优点::容易理解
- 缺点:三分支导致查找长度不均衡
- 不变性:只对A[mi]进行判断,直到区间长度为0
//二分查找(版本A)
int binSearch_A (int* A, int e, int lo, int hi){
while( lo < hi){
int mi = (lo + hi) >> 1;
if ( A[mi] < e) lo = mi + 1;
else if ( A[mi] > e) hi = mi;
else return mi;
}
return -1;//查找失败
}
2.2 斐波拉契查找版本A
- 斐波拉契查找需要调用"Fib.h"文件
- 优点:相对于二分查找版本A的改进是使用斐波那契数列中的数字作分割点,以此平衡两个分支的查找长度
//斐波拉契查找(版本A)
int fibSearch ( int* A, int const& e, int lo, int hi)
{
Fib fib ( hi - lo);
while ( lo < hi){
while ( hi - lo < fib.get()) fib.prev();
int mi = lo + fib.get() - 1;
if (e < A[mi]) hi = mi;
else if (A[mi] < e) lo = mi + 1;
else return mi;
}
return -1;//查找失败
}
class Fib{//Fibonacci数列类
private:
int f,g;
public:
Fib ( int n)
{f = 1;g = 0; while ( g < n) next();}
int get() { return g;}
int next() { g += f; f = g - f; return g;}//转至下一项,O(1)时间
int prev() { f = g - f; g -=f; return g;}//转至上一项,O(1)时间
};
3. 版本B——二分查找
- 优点:从三分支改进为两分支,自然地解决了版本A分支查找长度不均匀的弊端
- 缺点:不能指示失败的位置
- 不变性:采用减而治之的策略,保证e必然存在于[lo,hi)区间内。程序终点为lo+1=hi,最后只有A[lo]一个元素,对其判断即可
//二分查找(版本B)
int binSearch_B (int* A, int e, int lo, int hi){
// 结束条件为只剩一个元素 A[lo]
while( 1 < hi -lo ){
int mi = (lo + hi) >> 1;
(e < A[mi]) ? hi = mi: lo = mi;//[lo, hi)--[lo, mi) or [mi, hi) 减而治之
}
return ( e == A[lo]) ? lo : -1;
}//查找不到不能指示失败的位置
4. 版本C——二分查找
- 满足查找失败时返回不大于被查找数的最大元素秩的语义
- 不变性:A[0,lo)中元素不大于e,A[hi,n)内元素全都大于e。程序终点为lo = hi,此时A [lo] > e, A[lo-1]为不大于e的最大值
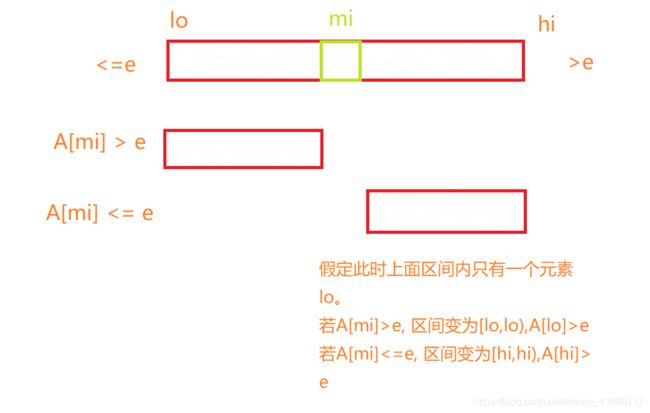
//二分查找(版本C)
int binSearch_C (int* A, int e, int lo, int hi){
// 结束条件为只剩一个元素 A[lo]
while( lo < hi ){
int mi = (lo + hi) >> 1;
(e < A[mi]) ? hi = mi: lo = mi + 1;//[lo, hi)--[lo, mi) or [mi, hi) 减而治之
}
return --lo;//lo-1是不大于e的最后一个元素
}//查找不到不能指示失败的位置
5. 总结
从三种版本的二分查找以及斐波那契查找可以看出,改进二分查找是一个非常细致的工作。各个版本其实区别不大,但是小小的改变能够导致语义与设计思想的完全不同。版本A的不变性在于不断比较A[mi],直到区间长度为0;版本B的不变性在于使得e包含在[lo,hi)中,直到区间长度减小为1,通过比较A[lo]来确定返回值;版本C的不变性在于每次的比较将一部分元素归于左边(小于等于e)或者右边(大于e)中去,最后结束于最后的一个元素被分配,区间长度变为0,此时的A[–lo]就是满足语义的那个元素。