【做练习】最大上升子序列(树状数组) 树状数组的原理及应用详解
1. 题目
总时间限制: 1000ms 内存限制: 65536kB
描述
一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4,比如子序列(1, 3, 5, 8).
你的任务,就是对于给定的序列,求出最长上升子序列的长度。
输入
输入的第一行是序列的长度N (1 <= N <= 300000)。第二行给出序列中的N个整数,这些整数的取值范围都在0到100000000之间。
输出
最长上升子序列的长度。
样例输入
7
1 7 3 5 9 4 8
样例输出
4
2. 分析
这是一道经典题,我们通常立刻想到动态规划来做。但是我们本题中序列的长度很大(300000),只有1000ms,动态规划的 O ( n 2 ) O(n^2) O(n2)复杂度肯定会TimeOut。
2.1. 树状数组
这里介绍另一办法:树状数组,它能够将复杂度降低到 O ( n l o g ( n ) ) O(n log(n)) O(nlog(n))。
树状数组是一种数组的特殊存储方式,它储存区间属性而不是每个元素。
2.1.1. 什么时候用树状数组?
我们假设数组的任意闭区间 A [ i : j ] A[i:j] A[i:j]具有属性 P ( A [ i : j ] ) P(A[i:j]) P(A[i:j]),并且,若我们把 A [ i : j ] A[i:j] A[i:j]划分为任意数量个子区间 A [ i : i 1 ] , A [ i 1 : i 2 ] , . . . , A [ i k : j ] A[i: i_1],A[i_1:i_2],...,A[i_k: j] A[i:i1],A[i1:i2],...,A[ik:j]后, P ( A [ i : j ] ) P(A[i:j]) P(A[i:j])总是可以由这些子区间的属性 P ( A [ i : i 1 ] ) , P ( A [ i 1 : i 2 ] ) , . . . , P ( A [ i k : j ] ) P(A[i: i_1]),P(A[i_1:i_2]),...,P(A[i_k:j]) P(A[i:i1]),P(A[i1:i2]),...,P(A[ik:j]) 推导得出。这时我们称这个数组对属性 P P P满足区间化条件(这个说法是我擅自定义的)。这时,我们就能够用树状数组(或线段树)来解决问题了。
常见的可满足区间化条件的属性有:区间求和、最值等。
2.1.2. 怎么建立树状数组?
我们设原来得到数组为 A A A,现在想要把它变为树状数组(记为 C C C),怎么做呢?为此,我们引入一个LowBit辅助函数。LowBit(x)把x除了最低非零位之外的所有位置零。换句画说,LowBit(x)计算一个尽可能大的2的幂,使得它为x的一个因数。注:假设A和C的下标均从1开始。
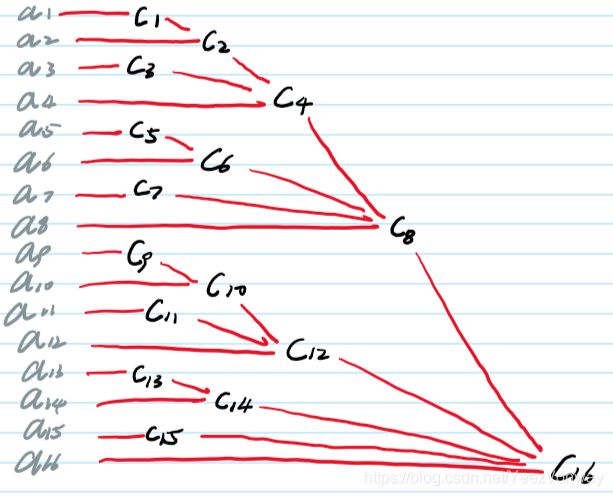
然后,我们用 C [ i ] C[i] C[i]来记录区间 A [ i − L o w B i t ( i ) + 1 : i ] A[i-LowBit(i)+1 : i] A[i−LowBit(i)+1:i]的区间属性。
以下示意图表示了一个 C C C和原数组区间的对应关系。
2.1.3. Ask操作
A s k ( i ) Ask(i) Ask(i)操作查询区间 A [ 1 : i ] A[1:i] A[1:i]的属性。
我们以求和为例,此时,我们只需要把 i i i写为: i = 2 k 1 + 2 k 2 + 2 k 3 + . . . + 2 k m i=2^{k_1} + 2^{k_2}+2^{k_3}+...+2^{k_m} i=2k1+2k2+2k3+...+2km,其中 k 1 > k 2 > . . . > k m k_1>k_2>...>k_m k1>k2>...>km
则 A [ 1 : i ] A[1:i] A[1:i]的求和即可写为 C [ 2 k 1 ] + C [ 2 k 1 + 2 k 2 ] + . . . + C [ 2 k 1 + 2 k 2 + . . . + 2 k m ] C[2^{k_1}]+C[2^{k_1}+2^{k_2}]+...+C[2^{k_1} + 2^{k_2}+...+2^{k_m}] C[2k1]+C[2k1+2k2]+...+C[2k1+2k2+...+2km]
具体如何做?其实很简单:
int Ask(i)
{
int sum = 0;
for(; i >= 1; i -= LowBit(i)) sum += C[i];
return sum;
}
我们还可以通过 A s k ( N ) Ask(N) Ask(N)来查询整个数组的属性。这个操作是 O ( l o g ( N ) ) O(log(N)) O(log(N))的。
2.1.4 Update操作
U p d a t e ( i , v a l u e ) Update(i, value) Update(i,value)操作更新某个区间的属性,并进一步更新包含这个区间的上层区间。这个操作也是 O ( l o g ( N ) ) O(log(N)) O(log(N))的。
如果我们记 H ( x ) = x + L o w B i t ( x ) H(x)=x+LowBit(x) H(x)=x+LowBit(x),我们发现,对于 C [ i ] C[i] C[i]所对应的区间,包含它的区间为: C [ i ] , C [ H ( i ) ] , C [ H ( H ( i ) ) ] , C [ H ( H ( H ( i ) ) ) ] , . . . C[i], C[H(i)], C[H(H(i))], C[H(H(H(i)))], ... C[i],C[H(i)],C[H(H(i))],C[H(H(H(i)))],...
同样以求和为例:
void Update(int i, int v)
{
int delta = v - C[i];
for(; i <= N; i += LowBit(i))
C[i] += delta;
}
使用树状数组解决最长上升子序列
在动态规划方法中,我们记对于结尾下标为 i i i(含)的最大上升子序列长度为 L I S ( i ) LIS(i) LIS(i), 它满足递推式:
L I S ( i ) = m a x { L I S ( j ) + 1 ∣ j < i ∧ A [ i ] ≤ A [ j ] } LIS(i)={max} \{ LIS(j) + 1 | jLIS(i)=max{LIS(j)+1∣j<i∧A[i]≤A[j]}
若对序列 L I S ( 1 ) , L I S ( 2 ) , . . . , L I S ( N ) LIS(1), LIS(2), ..., LIS(N) LIS(1),LIS(2),...,LIS(N)求取区间最大值,是满足区间化性质的,可以使用树状数组来储存。而且我们知道, m a x L I S [ i : j ] max\ LIS[i:j] max LIS[i:j]表示结尾落在区间 A [ i : j ] A[i:j] A[i:j]的最上升子序列。
如果我们首先把输入数组 A A A按照以下规则重新排序,得到 A ′ A' A′:
- 数值小的更靠前
- 数值相等时,保持在原数组中的先后顺序
我们从左到右扫描排序后的数组 A ′ A' A′,当扫描到 A ′ [ k ] A'[k] A′[k]时,维护树状数组 C [ i ] C[i] C[i]为:在只考虑扫描过的数字的前提下,从开始到位置 i i i的最大上升子序列。
设 A [ k ] A[k] A[k]排序后变为 A ′ [ k ′ ] A'[k'] A′[k′],那么,当扫描到 A ′ [ k ′ ] A'[k'] A′[k′]时,对于树状数组的维护,只需进行操作: U p d a t e ( k , A s k ( k ) + 1 ) Update(k, Ask(k)+1) Update(k,Ask(k)+1),即可。
代码
#include