【转载】ROI-Align 原理理解
---- 对背景问题的理解 -----
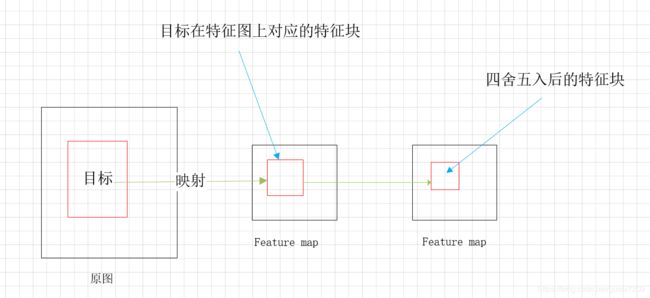
之前一直在想一个问题:一个Label在原图上标记出一个包含目标的区域。这个框在特征提取后,大小被缩小到了什么程度?
如果这个label框本身就不大,那么经过几层池化之后,是不是在最后的feature map上都没有一个位置,能够对应到这个区域?
目标在特征提取过程中,由于这种深度结构导致目标被【腐蚀】或者说该目标的特征被淹没。
这个问题更广义的描述:针对一个固定网络,多大的框(目标)才能在深度网络提取的特征中至少剩余一个明确的像素点,指向这个目标。
反过来看,也就是说最后一层的feature map上的一个点,映射回原图得到一片感受野,如果目标框比这个感受野还要小,会不会就是过度的特征提取?假设这个思路成立,可能这就是模型能力相对与不同大小的目标而言的一种模糊下界。
一直在调参,就把这个问题放在这里了。前天师兄让我帮他看看roi-align,扫了一眼发现,其实上面的问题跟align试图解决的问题很相似。不同的是,它不是假设小目标被【腐蚀】了。而是说这个目标其实还能对应上特征图上的某一个小点甚至是区域,但是因为量化问题,使得稍微的一点偏差,对于小目标的特征来说,都影响十足。就好像眼里掉入了一颗灰尘和眼里掉入了一颗小石子的区别。
下面说一说我的解读。
---------------------------
论文:https://arxiv.org/pdf/1703.06870.pdf Mask-RCNN
代码:https://github.com/matterport/Mask_RCNN
针对问题:roi-pooling的量化误差对小目标的影响
--------------------------
Roi-pooling的问题:
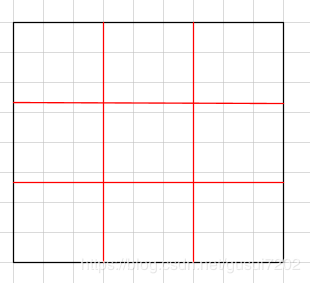
roi-pooling的输入是proposal的坐标,这些坐标由RPN计算得到,因为经过一次回归,所以跟原图上的proposal对应映射到feature map上是一个浮点数的坐标。可想而知,整个feature就是一叠矩阵,矩阵的下标不都是整数吗。所以映射过来的浮点数坐标要被向下取整,缩小为整数区域。如下图所示:可以明显的看到量化后的差异。
这还没到roi-pooling的步骤,只是获取Proposal对应的特征图。Roi-Pooling进行量化,如下图
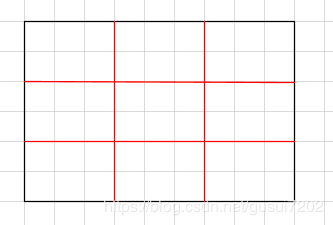
这是一个h*w=8*9的目标特征块,然后非要分成3x3,这样有一个边就不能整除,所以计算的时候roi-pooling再次量化如下
这下刚好够分了。但一个roi-pooling一共产生了两次量化误差。
Roi-Align的解决办法:
两次量化其实都是因为映射后坐标是浮点数,而特征值只在整数坐标上有。所以要量化。
Align两次都不量化,浮点数坐标就浮点数坐标吧。反正我只是计算,我又不按这个坐标去取feature map上的数值(浮点数的坐标在feature map上是没有值的)。
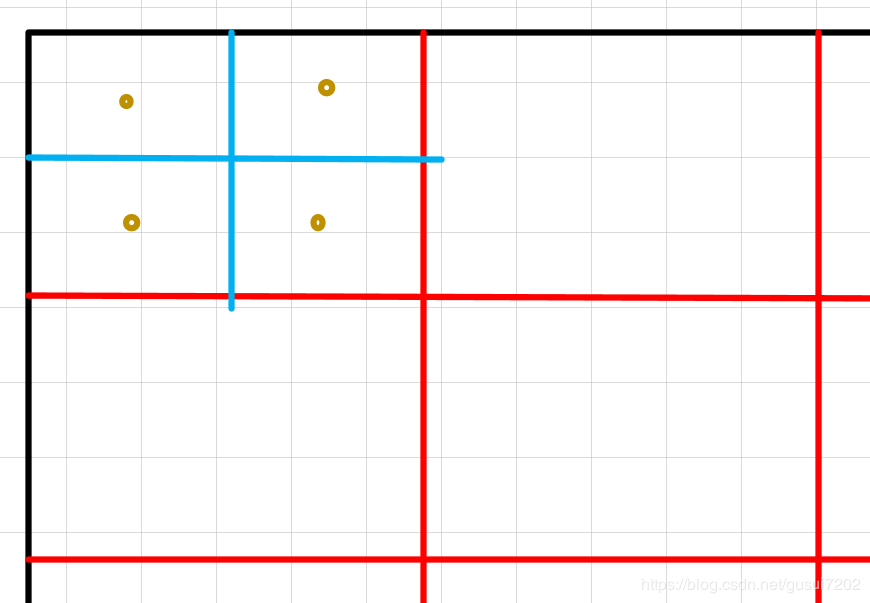
然后把浮点数坐标当成一个范围,范围的大小为浮点坐标 向上取整,得到两个整数坐标,画出一个规整的框,这个框里的所有特征都要用于计算roi-pooling。其实向上取整就能保证目标特征块不被缩小了,但这样引入了噪声呢。这个范围映射回原图对应的框应该是大于rpn得到的proposal的。引入了背景噪声。
所以计算的时候,用双线性插值,使得原图上任意一个浮点坐标,都将会有值。现在解决浮点坐标的取值问题了。然后怎么修改roi-pooling呢?计算roi-pooling在上图中分隔开的每一个小bin(一共3x3个,红线分出来的)的中心点,因为边界时浮点数,所以每一个中心点都时浮点数,然后用双线性插值得到这个浮点坐标的特征值。作为rop-pooling的结果。9个Bin格,9个中心点,9个特征值。ok,同样满足输入固定的要求,但是量化误差大大减小。
上面的例子为什么要取中心点?其实不一定要取中心点。作者在原文中发现,每一个Bin,划分为4个mini bin,计算每一个mini bin,上面的中心点对应的特征值。如下图所示:
就相当于每一个bin 得到一个2x2的矩阵,你可以取最大池化或者平均池化,把这四个数值像对特征图一样进行pooling,使得每一个Bin得到一个值,最后还是9个bin,得到固定输出3x3。
同样,你也可以取5、6、7、8、9个点,每一个浮点坐标因为双线性插值的缘故,都有取值。
Align反向传播的疑惑
roi-pooling的反向传播很好理解,最后用的最大池化,这个最大值来自于输入feature map的哪个像素,哪个像素就回传。但是Align这种不量化的就麻烦了,找不到对应的点啊,怎么办?范围。
如果我取的是中心点,那么回传的时候,这个浮点坐在原来的feature map上也是一个浮点坐标,我计算以这个坐标为中心,半径为1的圆,这个圆圈碰到的特征点都回传,原文好像说的是与这个点距离小于1的都回传,意思很明显了吧。
个人理解:
其实对于大目标来说,这些量化损失都在边上,丢那么一点点对目标的影响不大,但对于小目标影响就很大了。
并且我觉得回传的点,实际上是变多了。但也不能就此说计算量变大,还要具体计算才能知道。
--------------------------
个人理解有偏差。
---------------------
作者:南石北岸生
来源:CSDN
原文:https://blog.csdn.net/gusui7202/article/details/84799535
版权声明:本文为博主原创文章,转载请附上博文链接!