查找算法——分块查找 你掌握了吗?
齐心协力 一起抗疫
1.分块查找
分块查找又称索引顺序查找,是介于顺序查找和折半查找之间的查找算法,它是顺序查找算法的一种改进算法。
2.算法说明
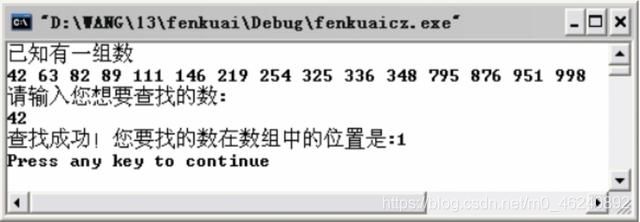
运行分块查找程序,系统会输出要查找的数组,提示用户输入想要查找的数。输入后系统判断并输出有无此数,如果该函数存在的话系统还会输出其在数组中的位置。程序运行结果如图所示。
3.算法分析
分块查找算法的描述是将n个数据元素“ 按块有序”划分为m块(m≤n)。每一块中的结点不必有序,但块与块之间必须“按块有序”;即第一 块中任一 元 素的关键字都必须小于第二块中任一元素的关键字; 而第二块中任一元素的关键字又都必须小于第三块中的任一元 素的关键…
操作步骤:
(1)选取各块中的最大关键字构成-一个索引表。
(2)查找分为两部分,先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中。
(3)然后,在已经确定的块中用顺序法进行查找。
分块查找的平均查找长度ASLbs。
分块查找是两次查找过程,整个查找过程的平均查找长度是两次查找的平均查找长度之和。其计算公式为:
ASLbs=Lb+Lw
其中Lb表示查找索引表以确定记录所在块的平均查找长度; Lw表示在查找到的块中, 查找记录的平均查找长度。
①以二分查找来确定块,分块查找成功时的平均查找长度ASLbs
=Lb+Lw
=lg(b+1)-1+(s+1)/2
=lg(n/s+1)+s/2。
②以顺序查找来确定块,分块查找成功时的平均查找长度ASLos=Lp+Lw
=(b+1)/2+(s+1)/2
= (s2+2s+n)/(2s)。
分块查找中块的大小:可根据表的特征进行分块,不一定要将线性表分成大小相等的若干块。各块可放在不同的向量中,也可将每一块存放在一个单链表中。
分块查找的优点:
(1)在表中插入或删除一个个 记录时,只要找到该记录所属的块,就在该块内进行插入和删除运算。
(2)因块内记录的存放是任意的,所以插入或删除比较容易,无须移动大量记录。分块查找算法的主要代价是增加一个辅助数组的存储空间。
实现过程
本程序实现过程如下:
(1)启动Microsoft Visual C++ 6.0。
(2)选择file/new菜单项,在弹出的对话框里选择files/C++ Source File选项,填写文件名,设置存储路径,单击OK按钮。
(3)编写程序代码。
定义结构体类型和变量,程序代码如下:
struct index
/*定义块的结构*/
int key;
int start;
int end;
} index[4];
/*定义结构体数组*/
变量定义并输出已知数组,程序代码如下:
int i,j=-1, k, key;
/*定义变量*/
int a[]={42,63,82,9,111,146,219,254,325,336,348,795,876,951,998};
/*已知的一组数*/
printf("已知有一组数\n");
for(i=0;i<15;i++)
printf("%d ",a[i]);
/*输出已知数组*/
printf("\n");
确认模块的起始值和最大值,程序代码如下:
for(i=0;i<3; i++)
{
index[i].start= j+1;
/*确定每个块范围的起始值*/
j=j+ 1;
index[i].end=j+4;
/*确定每个块范围的结束值*/
j=j+4;
index[i].key = a[j];
/*确定每个块范围中元素的最大值*/
}
输入要查询函数,并调用函数进行查找。程序代码如下:
printf(" 请输入您想要查找的数:\n");
scanf("%d", &key);
/*输入要查询的数值*/
k = search(key, a);
/*调用函数进行查找*/
输出查找结果,程序代码如下:
if(k>=0)
printf("查找成功!您要找的数字数组中的位置是:%d\n", k+1);
/*如果找到该数,则输出其位置*/
else
printf("查找失败!您要找的数不在数组中。\n");
/*若未找到则输出提示信息*/
}
定义函数search(实现分块查找,程序代码如下:
int search(int key, int a[])
/*自定义实现分块查找*/
{
int i,j;
i= 0;
while (i < 3 && key > index[i].key)
/*确定在哪个块中*/
i++;
if(i>=3);
/*大于分得的块数,则返回0*/
return -1;
j = index[i].start;
/*j等于块范围的起始值*/
while(i <= index[i].end && a[j] != key)
/*在确定的块内进行查找*/
j++;
if (i > index[i].end)
/*如果大于块范围的结束值,则说明没有要查找的数,j值0*/
j= -1;
return j;
}

或许命运有时候会不公,但只要我们努力地去奋斗,时刻谨记“奋斗”二字,我们就能“扼住命运的咽喉”,改写命运。 加油!!
扫描二维码
微信公众号:物达校园
让我知道你
再看
哦