顺序查找与"哨兵"的使用&&二分查找
查找:根据某个给定关键字X,从集合R中找出关键字与X相同的记录。
数组构成:
typedef struct LNode *List;
struct LNode{
ElementType Data[MAXSIZE];
int Last;//存储最后一个元素位置(记录长度)
}LNode;一. 顺序查找
- 1.不带“哨兵”的顺序查找
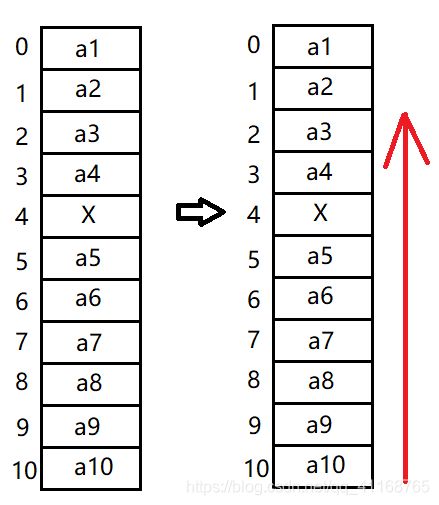
由于不带“哨兵”,数组的第一个位置(Data[0])用于存储数据,所以线性表的初始化中Last是从-1开始的,表示表中暂无元素。
/*初始化1
*实现功能:建立空的线性表
*传入形参:无
*返回值:线性表指针
*/
List MakeEmpty1()
{
List PtrL;
PtrL = (List)malloc(sizeof(LNode));
PtrL->Last = -1;//表示线性表中没有元素
return PtrL;
}相对应的查找函数如下:
/*顺序查找 (无"哨兵")
*函数功能:在Data[0]~Data[n]中查找关键字为X的数据元素
*传入形参:线性表指针 PtrL, 关键字 X
*返回值:查找成功返回所在单元下标,不成功返回 0
*/
int SequentialSearch1(List PtrL,ElementType X)
{
int i;
for(i = PtrL->Last; i > 0 && PtrL->Data[i] != X; i--);
return i;
}- 2.带“哨兵”的顺序查找
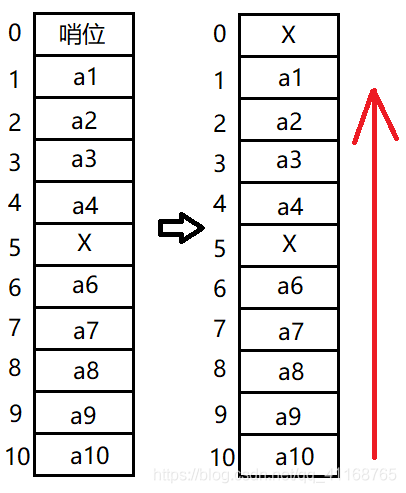
所谓“哨兵”就是用一个特殊值来作为数组的边界,使用“哨兵”可以少用一条判断语句,所以可以提高程序的效率。
这样就可以将数组的第一个位置作为“哨位”,数据的存储从Data[1]开始。因此线性表的初始化中Last是从0开始的,表示表中暂无元素。
/*初始化2
*实现功能:建立空的线性表
*传入形参:无
*返回值:线性表指针
*/
List MakeEmpty2()
{
List PtrL;
PtrL = (List)malloc(sizeof(LNode));
PtrL->Last = 0;//表示线性表中没有元素
return PtrL;
}相对应的查找函数如下:
/*顺序查找 (有"哨兵")
*函数功能:在Data[1]~Data[n]中查找关键字为X的数据元素
*传入形参:线性表指针 PtrL, 关键字 X
*返回值:查找成功返回所在单元下标,不成功返回 0
*/
int SequentialSearch2(List PtrL,ElementType X)
{
int i;
PtrL->Data[0] = X;//建立哨兵
for(i = PtrL->Last; PtrL->Data[i] != X; i--);//从后往前遍历查找
return i;
}将哨兵赋值为关键字X,这样判别条件便只有一个。并且同样当检索完的时候,会满足判别条件并返回“0”。
二. 二分查找(带哨兵)
二分查找,所针对的是有序数组,即数据在之前必须已经由小到大排序完成。
简单来说即通过寻找中间数并比较大小,确定目标数所在区间,并且不断通过这种方法缩小区间,直到找到目标数。
具体实现如下:
1. 通过Last确定左(left)右(right)边界,计算得出中间数位置(mid)。
2. 比较mid处的数与目标数X的大小,确定目标数所在区间(左半部分或右半部分或者该处就是X)。
3. (1)若X在左半部分,则将右边界right左移到mid的左边。再重新确定mid,重复1,2步骤。
(2)若X在右半部分,则将左边界left左移到mid的右边。再重新确定mid,重复1,2步骤。
(3)若X即为mid处的数,则返回mid的值。
该方法与“最大子列和”问题中“分而治之”的方法,有着异曲同工之妙。不同的是,在这个问题中,我们只需要要找到目标数的位置即可,所以通过“分”之后不需要两边都“治”,另一半部分直接舍弃。这样做较之顺序查找的方法便可大大增加查找效率。
下面通过一个例子来说明:
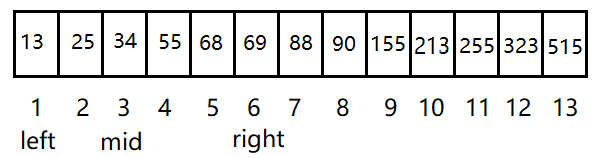
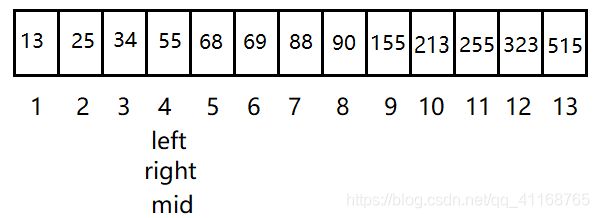
假如要从下面的数组中找数“55”
1. mid = (left + right)/2 = 14/2 = 7,此时mid位置上的数为 88 > 55. 55在左半部分,所以right = mid -1 = 6。
2. mid = (left + right)/2 = 7/2 = 3,此时mid位置上的数为34 < 55. 55在右半部分,所以left = mid + 1 = 4。
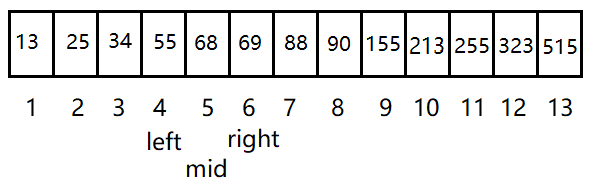
3. mid = (left + right)/2 = 10/2 = 5,此时mid位置上的数为68 > 55. 55在左半部分,所以right = mid - 1 = 4。
4. mid = (left + right)/2 = 8/2 = 4,此时mid位置上的数为55.成功找到目标数55的位置,返回mid的值。
那如果查找的数不在该数组内时,情况会如何呢?
如上例中如果我们要找的目标数为“42”,当进行到3时,mid位置上的数为55 > 42.
程序会判定42在左半部分,所以更改右边界right的值,right = mid - 1 = 3
此时,left = 4;right = 3;右边界(right)到了左边界(left)的左边,说明查找完毕。没找到42,返回 -1。
由此我们便可以知道,循环的截至条件为 left > right。
程序如下:
/*二分查找 (有"哨兵")
*函数功能:在Data[1]~Data[n]中查找关键字为X的数据元素
*传入形参:线性表指针 PtrL, 关键字 X
*返回值:查找成功返回所在单元下标,不成功返回 -1
*/
int BinarySearch(List PtrL,ElementType X)
{
int left,right,mid;
int NoFound = -1;
left = 1;
right = PtrL->Last;
while(left <= right){
mid = (left + right)/2;//计算中间元素坐标
if(X < PtrL->Data[mid]) right = mid - 1;//目标在左半部分,调整右边界
else if(X > PtrL->Data[mid]) left = mid + 1;// 目标在右半部分,调整左边界
else return mid;//目标即在 mid
}
return NoFound;
}测试主函数如下:
#include
#include
#define MAXSIZE 100
typedef int ElementType;
typedef struct LNode *List;
struct LNode{
ElementType Data[MAXSIZE];
int Last;
}LNode;
int SequentialSearch1(List PtrL,ElementType X);
int SequentialSearch2(List PtrL,ElementType X);
List MakeEmpty1();
List MakeEmpty2();
int BinarySearch(List PtrL,ElementType X);
int main()
{
int i;
int X;
List L;
printf("不带哨兵的顺序查找\n");
L = MakeEmpty1(); //不带哨兵的初始化
printf("输入元素:");
do{
scanf("%d",&L->Data[L->Last+1]);
L->Last++;
if(getchar() == '\n')
break;
}while(1);
printf("输入查找的数:");
scanf("%d",&X);
printf("Position:%d\n",SequentialSearch1(L,X));
free(L);
getch();
L = MakeEmpty2();//带哨兵的初始化
printf("输入元素(递增输入):");
do{
scanf("%d",&L->Data[L->Last+1]);
L->Last++;
if(getchar() == '\n')
break;
}while(1);
printf("带哨兵的顺序查找\n");
printf("输入查找的数:");
scanf("%d",&X);
printf("Position:%d\n",SequentialSearch1(L,X));
printf("二分查找\n");
printf("输入查找的数:");
scanf("%d",&X);
printf("Position:%d",BinarySearch(L,X));
free(L);
} 测试结果如下:
测试环境:win10 使用软件:DEV_C++
参考文献:何钦铭,《数据结构讲义》,浙江大学