数据结构中的查找(顺序查找、折半查找、分块查找)
查找,就是根据给定的某个值在一组记录集合中确定某个“特定的”数据元素(记录)或者找到属性值符合特定条件的某些记录。
查找表是由同一类型的数据元素(或记录)构成的集合。
关键字:是数据元素(或记录)中某个数据项的值,用以标识(识别)一个数据元素(或记录)。
主关键字:可以识别唯一的一个记录的关键字。
次关键字:可以识别若干记录的关键字。
对查找表常进行的操作:
(1)查询某个“特定的”数据元素是否在查找表中
(2)检索某个“特定的”数据元素的各种属性
(3)在查找表中插入一个数据元素
(4)从查找表中删去某个数据元素
一般(1)(2)称为静态查找,(3)(4)称为动态查找。
查找的方法取决于查找表的结构。
- 比较式查找
(1)基于线性表的查找
顺序查找、折半查找、分块查找
(2)基于树的查找
二叉排序树、B树、AVL树
分析查找的时间性能:
查找算法的平均查找长度(Average Search Length)
为确定记录在查找表中的位置,需和给定值进行比较的关键字个数的期望值(查找成功时)
ASL = ∑I=1nPiCi
其中:
n为表长;
Pi为查找表中第个记录的概率,且∑I=1nPi = 1;
Ci为找到该记录时,曾和给定值比较过的关键字的次数。
顺序查找
顺序查找表的数据类型描述为:
#define MAXSIZE 1000//顺序查找表记录数目
typedef int Key Type;//假设关键字类型为整型
typedef struct{
KeyType key;//关键字项OtherType
other_data;//其他数据项
}Record Type;
//记录类型
typedef struct{
RecordType r[MAXSIZE+1];
int length;//序列长度,即实际记录个数
}SeqRList;//记录序列类型,即顺序表类型
SeqRList L;//L为一个顺序查找表
顺序查找算法:
int SeqSearch(RecordList 1, Key Type k){
int i;
i=l.length;
while(i>=1&&1.r[i].key!=k)
i--;
if(i>=1) return(i);
else return(0);
}
改进后的查找算法(使用0号位置作为监视哨,记录待查的关键字):
int SeqSearch(RecordList l,Key Type k){
int i;
l.rl0].key=k; /*标识边界*/
i=l.length;
while(l.r[i].key!=k)
i--;
return(i);
}
对顺序表而言,ASL=nP1+(n-1)P2+……+2Pn-1+Pn,
在等概率查找的情况下,顺序表查找成功的平均查找长度为:Pi=1/n ,Ci=n-i+1
查找成功时的平均查找次数公式如下,几乎是表长的一半。当表长特别大的时候,这个查找效率就非常低了。

若查找概率无法事先测定,则查找过程采取的改进办法是,附设一个访问频度域或者在每次查找之后,将刚刚查找到的记录直接移至表尾的位置上。
折半查找
思路
设定查找范围的下限low,上限high,由此确定查找范围的中间位置mid;
中间位置的值等于待查的值,查找成功;
中间位置的值小于待查的值,low=mid+1;
中间位置的值大于待查的值,high=mid-1。
int BinSrch(RecordList l,KeyType k){
int low=1,high=l.length,mid;
while(low<=high){
mid=(low+high)/2;
if(k==l.r[mid].key) return mid;
else if(k<l.r[mid].key) high=mid-1;
else low=mid+1;
}
return 0;
}
折半查找是典型的分治类算法,所以算法也可以利用递归来实现。
平均查找长度
可以用判定树来进行分析。判定树中每一个结点对应表中的一个记录,该记录是在表中的位置序号。方块出现的位置就是查找失败的位置。根结点对应区间的中间位置。左子树对应前半部分子表,右子树对应后半部分子表。
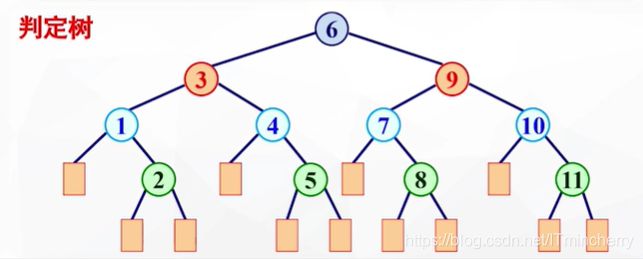
找到有序表中任一记录的过程就是走了一条从根结点到与该记录相应的结点的路径;
给定值进行比较的关键字个数恰是该结点在判定树上的层次数。
折半查找成功时,最多的比较次数不会超过判定树的深度。由于判定树的叶子结点所在层次之差最多为1,所以含有n个结点的判定树的深度与n个结点的完全二叉树的深度相等,均为(向下取整)[log2n]+1。由此,折半查找成功时,关键字的比较次数最多不会超过数最多不超过[log2n]+1。折半查找失败时,关键字比较次数最多也不超过判定树的深度[log2n]+1。
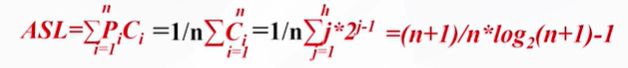
ASL = (n+1)/n*log2(n+1)-1
假设n=2h-1并且查找概率相等,则:在n>50时,可得近似结果 ≈ log2(n+1)-1
折半查找的优点在于:
关键字的查找次数较少,查找速度较快,平均性能好;
但是缺点是要求待查的表必须为有序表,基于顺序存储结构,对于插入、删除操作来说,比较困难。
因此,折半查找适用于一经建立,就很少改动,又需要经常查找的表。
分块查找
分块查找,又称为索引顺序查找,吸取了顺序查找和折半查找各自的优点,既有动态结构,又适合快速查找。
基本思想:将查找表分为若干个子块。块内元素可以无序,但块与块之间必须"按块有序",每个块内的最大元素小于下一块所有元素的任意一个值。在建立一个索引表,索引表中的每个元素含有各块的最大关键字和各块中第一个元素的地址,索引表按关键字有序排列。
分块查找的过程:先在索引表中确定待查记录所在的块,可以顺序查找或者折半查找索引表;然后根据所在块的索引开始位置在块内顺序查找。
例如,关键字集合为{88,24,72,61,21,6,32,11,8,31,22,83,78,54},按照关键码值为24、54、78、88,分为四个块和索引表:

分块查找的平均查找长度为索引查找和块内查找的平均长度之和,设索引查找和块内查找 的平均查找长度分别为L1,Ls,则分块查找的平均查找长度为: ASL=L1+Ls
设将长度为n的查找表均匀的分为b块,每块有s个记录,在等概率的情况下,若在块内和索引表中均采用顺序查找,则平均查找长度为
![]()
此时,若s=√n,则平均查找长度去最小值:√n+1;若对索引表采用折半查找时,则平均查找长度为:
ASL=L1+Ls=⌈log2(b+1)⌉+(s+1)/2