cs224n学习5：homework1 Exploring Word Vectors

所用到的数据集，nltk_data里的reuters，
gensim-data里的GoogleNews-vectors-negative300
可自行下载

导入包：

# All Import Statements Defined Here
# Note: Do not add to this list.
# All the dependencies you need, can be installed by running .
# ----------------

import sys
assert sys.version_info[0]==3
assert sys.version_info[1] >= 5

from gensim.models import KeyedVectors
from gensim.test.utils import datapath
import pprint
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 5]

#导入nltk，并下载新闻数据集
import nltk
nltk.download('reuters')
from nltk.corpus import reuters
import numpy as np
import random
import scipy as sp

#降维
from sklearn.decomposition import TruncatedSVD
from sklearn.decomposition import PCA

#设置token
START_TOKEN = ''
END_TOKEN = ''

#设置相同的seed，使每次生成的随机数相同
np.random.seed(0)
random.seed(0)
# ----------------

单词向量通常被用作下游NLP任务的基本组成部分，例如回答问题、生成文本、翻译等，因此对它们的优缺点建立一些直觉是很重要的。在这里，您将探索两种类型的单词向量:从共现矩阵派生的单词向量，以及通过word2vec派生的单词向量。

Part 1: Count-Based Word Vectors

Co-Occurrence：
共现矩阵计算某些环境中事物同时发生的频率。考虑到文档中出现了一些单词，我们考虑围绕的上下文窗口。假设我们的固定窗口大小是，那么这就是文档中的前两个单词，即单词-…−1和+1…+。我们建立了一个共现矩阵，它是一个对称的逐字矩阵，其中是出现在窗口内的次数。
Example: Co-Occurrence with Fixed Window of n=1:

Document 1: “all that glitters is not gold”

Document 2: “all is well that ends well”

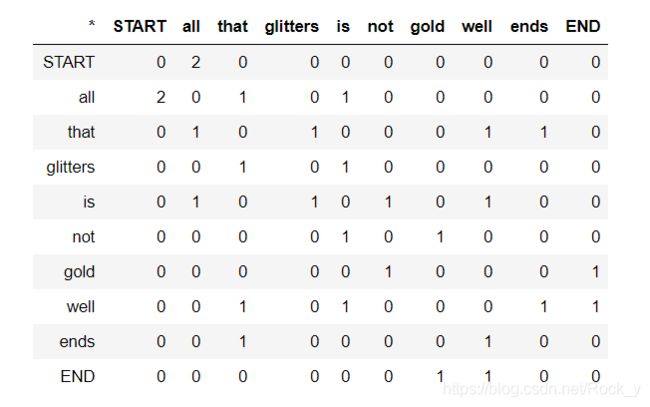
注意:在NLP中，我们经常添加 START and END符号来表示句子、段落或文档的开始和结束。在这种情况下，我们想象开始和结束标记封装每个文档，例如，“开始所有闪光的不是黄金的结束”，并包括这些标记在我们的共现计数。
这个矩阵的行（或列）提供了一种类型的词向量（基于词-词共现的词向量），但向量通常很大（语料库中不同单词的数量呈线性）。因此，我们的下一步是运行降维。特别地，我们将运行SVD（奇异值分解），这是一种广义PCA（主成分分析）来选择顶部主成分。这是一个用奇异值分解实现维数缩减的可视化。在这幅图中，我们的共现矩阵是，其中行对应于字。我们得到了一个完整的矩阵分解，奇异值排序在对角矩阵中，新的、较短长度的-字向量在中。

这种降维共现表示保留了单词之间的语义关系，例如doctor和hospital比doctor和dog更接近。
Plotting Co-Occurrence Word Embeddings：

#定义read_corpus函数，在输入语句的前后分别加 START 和 END ,并将所有的字母改为小写
def read_corpus(category="crude"):
    """ Read files from the specified Reuter's category.
        Params:
            category (string): category name
        Return:
            list of lists, with words from each of the processed files
    """
    files = reuters.fileids(category)
    return [[START_TOKEN] + [w.lower() for w in list(reuters.words(f))] + [END_TOKEN] for f in files]

reuters_corpus = read_corpus()
pprint.pprint(reuters_corpus[:3], compact=True, width=100)

Question 1.1: Implement distinct_words

编写一个方法来找出出现在语料库中的不同单词(单词类型)。

def distinct_words(corpus):
    """ Determine a list of distinct words for the corpus.
        Params:
            corpus (list of list of strings): corpus of documents  
            文档语料库
        Return:
            corpus_words (list of strings): list of distinct words across the corpus, sorted (using python 'sorted' function)
            整个语料库中不同单词列表
            num_corpus_words (integer): number of distinct words across the corpus
            整个语料库中不同单词数量
            
    """
    corpus_words = []
    num_corpus_words = -1
    
    # ------------------
    # Write your implementation here.
    
     #首先将corpus中的多个list压成一个list的形式
    corpus = [w for _ in corpus for w in _]
    #利用set中不含重复元素的性质保留corpus中不同的单词，再使用lsit()将结果转化为list的形式
    corpus_words = list(set(corpus))
    #使用内置的排序函数sorted()按字母的升序方式进行排序
    corpus_words = sorted(corpus_words)
    #使用len()获取list的长度
    num_corpus_words = len(corpus_words)

    # ------------------
    print(corpus_words[:], num_corpus_words)
    return corpus_words, num_corpus_words

# ---------------------
# Run this sanity check
# Note that this not an exhaustive check for correctness.
# ---------------------

# Define toy corpus
test_corpus = ["START All that glitters isn't gold END".split(" "), "START All's well that ends well END".split(" ")]
test_corpus_words, num_corpus_words = distinct_words(test_corpus)

# Correct answers
ans_test_corpus_words = sorted(list(set(["START", "All", "ends", "that", "gold", "All's", "glitters", "isn't", "well", "END"])))
ans_num_corpus_words = len(ans_test_corpus_words)

# Test correct number of words  测试正确的单词数量
assert(num_corpus_words == ans_num_corpus_words), "Incorrect number of distinct words. Correct: {}. Yours: {}".format(ans_num_corpus_words, num_corpus_words)

# Test correct words  测试正确的单词
assert (test_corpus_words == ans_test_corpus_words), "Incorrect corpus_words.\nCorrect: {}\nYours:   {}".format(str(ans_test_corpus_words), str(test_corpus_words))

# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

Question 1.2: Implement compute_co_occurrence_matrix

编写一个方法，构造一个特定窗口大小（默认值为4）的共现矩阵，考虑窗口中心单词前和后的单词。这里，我们开始使用numpy（np）来表示向量、矩阵和张量。如果您不熟悉NumPy，在cs231n Python NumPy教程的后半部分有一个NumPy教程。

def compute_co_occurrence_matrix(corpus, window_size=4):
    """ Compute co-occurrence matrix for the given corpus and window_size (default of 4).
        计算给定语料库和窗口大小(默认为4)的共现矩阵。
    
        Note: Each word in a document should be at the center of a window. Words near edges will have a smaller
              number of co-occurring words. 
              文档中的每个单词都应该位于窗口的中央。靠近边缘的单词会有更少的同时出现的单词。
              
              For example, if we take the document "START All that glitters is not gold END" with window size of 4,
              "All" will co-occur with "START", "that", "glitters", "is", and "not".
              例如，如果我们取窗口大小为4的文档“START All that glitters is not gold END”，
              “All”将与“START”、“that”、“glitters”、“is”和“not”同时出现。
    
        Params:
            corpus (list of list of strings): corpus of documents 文档的语料库
            window_size (int): size of context window 上下文窗口的大小
        Return:
            M (numpy matrix of shape (number of corpus words, number of corpus words)): M(形状的numpy矩阵(语料库词数，语料库词数)):
                Co-occurence matrix of word counts. 
                The ordering of the words in the rows/columns should be the same as the ordering of the words given by the distinct_words function.
                行/列中单词的顺序应该与distinct_words函数给出的单词的顺序相同。
            word2Ind (dict): dictionary that maps word to index (i.e. row/column number) for matrix M.
            将单词映射到矩阵M的索引(即行/列号)的字典。
    """
    words, num_words = distinct_words(corpus)
    M = None
    word2Ind = {}
    
    # ------------------
    # Write your implementation here.
    
    #定义一个空的词共现矩阵，这里采用零矩阵，因为M为对称阵，所以尺寸为num_words * num_words
    M = np.zeros(shape = (num_words,num_words),dtype = np.int32)
    
    #建立words中词和索引的映射关系，将其存到字典word2Int
    for i in range(num_words):
        word2Ind[words[i]] = i
    
    #对corpus中的每一部分分别进行处理
    for sent in corpus:
        for p in range(len(sent)):
            #找到当前sent中的词在word2Ind中的索引
            ci = word2Ind[sent[p]]
        
            #前
            #因为某些位置前面词的个数可能会小于window_size，所以如果个数小与window_size就从头开始
            for w in sent[max(0,p-window_size):p]:
                wi = word2Ind[w]
                M[ci][wi] += 1 
            
            #后
            for w in sent[p + 1:p + 1 + window_size]:
                wi = word2Ind[w]
                M[ci][wi] += 1
    # ------------------

    return M, word2Ind

# ---------------------
# Run this sanity check
# Note that this is not an exhaustive check for correctness.
# ---------------------

# Define toy corpus and get student's co-occurrence matrix
test_corpus = ["START All that glitters isn't gold END".split(" "), "START All's well that ends well END".split(" ")]
M_test, word2Ind_test = compute_co_occurrence_matrix(test_corpus, window_size=1)

# Correct M and word2Ind
M_test_ans = np.array( 
    [[0., 0., 0., 1., 0., 0., 0., 0., 1., 0.,],
     [0., 0., 0., 1., 0., 0., 0., 0., 0., 1.,],
     [0., 0., 0., 0., 0., 0., 1., 0., 0., 1.,],
     [1., 1., 0., 0., 0., 0., 0., 0., 0., 0.,],
     [0., 0., 0., 0., 0., 0., 0., 0., 1., 1.,],
     [0., 0., 0., 0., 0., 0., 0., 1., 1., 0.,],
     [0., 0., 1., 0., 0., 0., 0., 1., 0., 0.,],
     [0., 0., 0., 0., 0., 1., 1., 0., 0., 0.,],
     [1., 0., 0., 0., 1., 1., 0., 0., 0., 1.,],
     [0., 1., 1., 0., 1., 0., 0., 0., 1., 0.,]]
)
word2Ind_ans = {'All': 0, "All's": 1, 'END': 2, 'START': 3, 'ends': 4, 'glitters': 5, 'gold': 6, "isn't": 7, 'that': 8, 'well': 9}

# Test correct word2Ind
assert (word2Ind_ans == word2Ind_test), "Your word2Ind is incorrect:\nCorrect: {}\nYours: {}".format(word2Ind_ans, word2Ind_test)

# Test correct M shape
assert (M_test.shape == M_test_ans.shape), "M matrix has incorrect shape.\nCorrect: {}\nYours: {}".format(M_test.shape, M_test_ans.shape)

# Test correct M values
for w1 in word2Ind_ans.keys():
    idx1 = word2Ind_ans[w1]
    for w2 in word2Ind_ans.keys():
        idx2 = word2Ind_ans[w2]
        student = M_test[idx1, idx2]
        correct = M_test_ans[idx1, idx2]
        if student != correct:
            print("Correct M:")
            print(M_test_ans)
            print("Your M: ")
            print(M_test)
            raise AssertionError("Incorrect count at index ({}, {})=({}, {}) in matrix M. Yours has {} but should have {}.".format(idx1, idx2, w1, w2, student, correct))

# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

Question 1.3: Implement reduce_to_k_dim

构造一种方法，对矩阵进行降维以产生k维的嵌入。使用SVD取顶部的k个分量，并产生一个新的k维嵌入矩阵。

def reduce_to_k_dim(M, k=2):
    """ Reduce a co-occurence count matrix of dimensionality (num_corpus_words, num_corpus_words)
        to a matrix of dimensionality (num_corpus_words, k) using the following SVD function from Scikit-Learn:
            - http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.TruncatedSVD.html
    
        Params:
            M (numpy matrix of shape (number of corpus words, number of corpus words)): co-occurence matrix of word counts
            k (int): embedding size of each word after dimension reduction
            降维后每个单词的嵌入大小
        Return:
            M_reduced (numpy matrix of shape (number of corpus words, k)): matrix of k-dimensioal word embeddings.
            k维词嵌入矩阵。
                    In terms of the SVD from math class, this actually returns U * S
    """    
    n_iters = 10     # Use this parameter in your call to `TruncatedSVD`
    M_reduced = None
    print("Running Truncated SVD over %i words..." % (M.shape[0]))
    
        # ------------------
        # Write your implementation here.
        
        #导入TruncatedSVD函数
    svd = TruncatedSVD(n_components = k)
    svd.fit(M.T)
    M_reduced = svd.components_.T

        # ------------------

    print("Done.")
    return M_reduced

# ---------------------
# Run this sanity check
# Note that this not an exhaustive check for correctness 
# In fact we only check that your M_reduced has the right dimensions.
# ---------------------

# Define toy corpus and run student code
test_corpus = ["START All that glitters isn't gold END".split(" "), "START All's well that ends well END".split(" ")]
M_test, word2Ind_test = compute_co_occurrence_matrix(test_corpus, window_size=1)
M_test_reduced = reduce_to_k_dim(M_test, k=2)

# Test proper dimensions
assert (M_test_reduced.shape[0] == 10), "M_reduced has {} rows; should have {}".format(M_test_reduced.shape[0], 10)
assert (M_test_reduced.shape[1] == 2), "M_reduced has {} columns; should have {}".format(M_test_reduced.shape[1], 2)

# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

Question 1.4: Implement plot_embeddings

这里你要写一个函数来画出二维空间中的二维向量。对于图，我们将使用Matplotlib (plt)。

def plot_embeddings(M_reduced, word2Ind, words):
    """ Plot in a scatterplot the embeddings of the words specified in the list "words".
        NOTE: do not plot all the words listed in M_reduced / word2Ind.
        Include a label next to each point.
        在散点图中绘制“words”列表中指定的单词的嵌入。
        
        Params:
            M_reduced (numpy matrix of shape (number of unique words in the corpus , k)): matrix of k-dimensioal word embeddings
            word2Ind (dict): dictionary that maps word to indices for matrix M
            words (list of strings): words whose embeddings we want to visualize
    """

    # ------------------
    # Write your implementation here.
    
    for _ in words:
        x = M_reduced[word2Ind[_]][0]
        y = M_reduced[word2Ind[_]][1]
        #画散点图
        plt.scatter(x,y,marker= 'x')
        plt.text(x,y,_)
    plt.show()

    # ------------------

# ---------------------
# Run this sanity check
# Note that this not an exhaustive check for correctness.
# The plot produced should look like the "test solution plot" depicted below. 
# ---------------------

print ("-" * 80)
print ("Outputted Plot:")

M_reduced_plot_test = np.array([[1, 1], [-1, -1], [1, -1], [-1, 1], [0, 0]])
word2Ind_plot_test = {'test1': 0, 'test2': 1, 'test3': 2, 'test4': 3, 'test5': 4}
words = ['test1', 'test2', 'test3', 'test4', 'test5']
plot_embeddings(M_reduced_plot_test, word2Ind_plot_test, words)

print ("-" * 80)

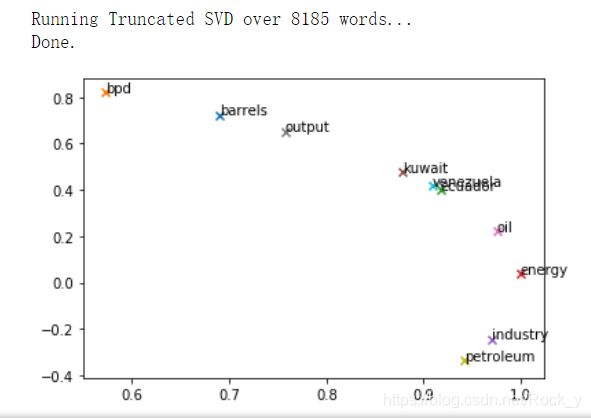
Question 1.5: Co-Occurrence Plot Analysis

现在我们将把你写的所有部分放在一起!我们将在Reuters“crude”语料库上计算固定窗口为4的共现矩阵。然后使用TruncatedSVD计算每个单词的二维嵌入。TruncatedSVD返回U*S，因此我们对返回的向量进行归一化，使所有的向量都出现在单位圆的周围(因此亲密是方向上的亲密)。

# -----------------------------
# Run This Cell to Produce Your Plot
# ------------------------------
reuters_corpus = read_corpus()
M_co_occurrence, word2Ind_co_occurrence = compute_co_occurrence_matrix(reuters_corpus)
M_reduced_co_occurrence = reduce_to_k_dim(M_co_occurrence, k=2)

# Rescale (normalize) the rows to make them each of unit-length
M_lengths = np.linalg.norm(M_reduced_co_occurrence, axis=1)
M_normalized = M_reduced_co_occurrence / M_lengths[:, np.newaxis] # broadcasting

words = ['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'venezuela']
plot_embeddings(M_normalized, word2Ind_co_occurrence, words)

Part 2: Prediction-Based Word Vectors

正如在课堂上讨论的那样，最近更流行的基于谓词的单词向量，例如word2vec。在这里，我们将探讨word2vec生成的嵌入。请重新阅读课堂笔记和幻灯片以获得更多关于word2vec算法的细节。如果你想冒险，挑战一下自己，试着阅读原文。
然后运行以下单元格将word2vec向量加载到内存中。注意:这可能需要几分钟。

def load_word2vec():
    """ Load Word2Vec Vectors
        Return:
            wv_from_bin: All 3 million embeddings, each lengh 300
    """
    import gensim.downloader as api
    wv_from_bin = api.load("word2vec-google-news-300")
    vocab = list(wv_from_bin.vocab.keys())
    print("Loaded vocab size %i" % len(vocab))
    return wv_from_bin

# -----------------------------------
# Run Cell to Load Word Vectors
# Note: This may take several minutes
# -----------------------------------
wv_from_bin = load_word2vec()

上述代码出现了一些问题，
所以改变方法。

def load_word2vec(embeddings_fp="C:\\Users\\17869\\gensim-data./GoogleNews-vectors-negative300.bin"):
    """ Load Word2Vec Vectors
        Param:
            embeddings_fp (string) - path to .bin file of pretrained word vectors
        Return:
            wv_from_bin: All 3 million embeddings, each lengh 300
                This is the KeyedVectors format: https://radimrehurek.com/gensim/models/deprecated/keyedvectors.html
    """
    embed_size = 300
    print("Loading 3 million word vectors from file...")
    ## 自己下载的文件
    wv_from_bin = KeyedVectors.load_word2vec_format(embeddings_fp, binary=True)
    vocab = list(wv_from_bin.vocab.keys())
    print("Loaded vocab size %i" % len(vocab))
    return wv_from_bin
wv_from_bin = load_word2vec()
print()

减少Word2Vec单词嵌入的维数：
让我们直接比较word2vec嵌入和共现矩阵的嵌入。运行以下单元格:

1.将300万个word2vec向量放入矩阵M中

2.运行reduce_to_k_dim(被截断的SVD函数)将向量从300维减少到2维。

def get_matrix_of_vectors(wv_from_bin, required_words=['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'venezuela']):
    """ Put the word2vec vectors into a matrix M.
        将word2vec向量放入矩阵M中。
        Param:
            wv_from_bin: KeyedVectors object; the 3 million word2vec vectors loaded from file
            从文件中加载的300万个word2vec向量
        Return:
        
            M: numpy matrix shape (num words, 300) containing the vectors
            M:包含向量的numpy矩阵形状(num字，300)
            word2Ind: dictionary mapping each word to its row number in M
            word2Ind:字典将每个单词映射到它在M中的行号
    """
    import random
    words = list(wv_from_bin.vocab.keys())
    print("Shuffling words ...")
    random.shuffle(words)
    words = words[:10000]
    print("Putting %i words into word2Ind and matrix M..." % len(words))
    word2Ind = {}
    M = []
    curInd = 0
    for w in words:
        try:
            M.append(wv_from_bin.word_vec(w))
            word2Ind[w] = curInd
            curInd += 1
        except KeyError:
            continue
    for w in required_words:
        try:
            M.append(wv_from_bin.word_vec(w))
            word2Ind[w] = curInd
            curInd += 1
        except KeyError:
            continue
    M = np.stack(M)
    print("Done.")
    return M, word2Ind

# -----------------------------------------------------------------
# Run Cell to Reduce 300-Dimensinal Word Embeddings to k Dimensions
#运行单元格将300维的单词嵌入减少到k维
# Note: This may take several minutes
# -----------------------------------------------------------------
M, word2Ind = get_matrix_of_vectors(wv_from_bin)
M_reduced = reduce_to_k_dim(M, k=2)

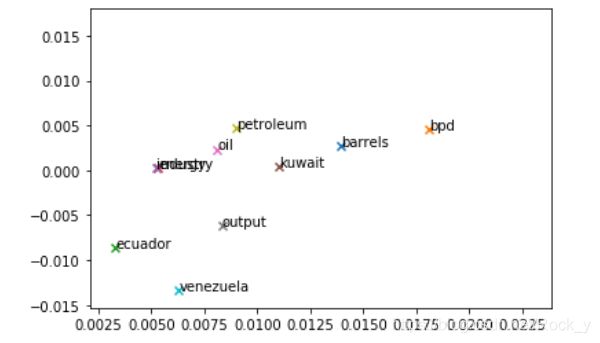
Question 2.1: Word2Vec Plot Analysis

运行下面的单元格，绘制[‘barrels’, ‘bpd’, ‘ecuador’, ‘energy’, ‘industry’, ‘kuwait’, ‘oil’, ‘output’, ‘petroleum’, ‘venezuela’]的2D word2vec嵌入图。

words = ['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'venezuela']
plot_embeddings(M_reduced, word2Ind, words)

Cosine Similarity 余弦相似度：
现在我们有了单词向量，我们需要一种方法来根据这些向量量化单个单词之间的相似性。其中一个度量是余弦相似度。我们将用它来寻找彼此“接近”和“远离”的单词。

我们可以把n维向量想象成n维空间中的点。如果我们采用这种观点，L1和L2距离有助于量化在这两点之间“我们必须走”的空间量。另一种方法是研究两个向量之间的夹角。从三角学中我们知道:

Question 2.2: Polysemous Words 多义词

找出一个多义词(例如，“叶子”或“勺子”)，使前10个最相似的词(根据余弦相似度)包含两个意思的相关词。例如，“leaves”(叶子)在前10名中有“vanishes”(消失)和“茎秆”(茎秆)，“scoop(勺子)”(勺子)有“handed_waffle_cone(华夫饼)”和“lowdown (lowdown)”。在你找到一个多义词之前，你可能需要尝试几个多义词

# ------------------
# Write your polysemous word exploration code here.

wv_from_bin.most_similar("women")

# ------------------

这里选用“women”，最相似的词如下

Question 2.3: Synonyms & Antonyms 同义词和反义词

在考虑余弦相似度时，考虑余弦距离通常更方便，即1 -余弦相似度。

找出三个单词(w1,w2,w3)，其中w1和w2是同义词，w1和w3是反义词，但是余弦距离(w1,w3) <余弦距离(w1,w2)。例如，w1=“快乐”比w2=“快乐”更接近于w3=“悲伤”。

# ------------------
# Write your synonym & antonym exploration code here.

w1 = "happy"
w2 = "cheerful"
w3 = "sad"
w1_w2_dist = wv_from_bin.distance(w1, w2)
w1_w3_dist = wv_from_bin.distance(w1, w3)

print("Synonyms {}, {} have cosine distance: {}".format(w1, w2, w1_w2_dist))
print("Antonyms {}, {} have cosine distance: {}".format(w1, w3, w1_w3_dist))

# ------------------

Solving Analogies with Word Vectors（用单词向量解决类比）：
Word2Vec向量有时显示出解决类比的能力。
举个例子，“男人:国王::女人:x”这个比喻，x是什么?
在下面的单元格中，我们向您展示了如何使用单词向量来查找x。most_similar函数查找与positive列表中单词最相似、与negative列表中单词最不相似的单词。这个类比的答案将是排名最相似的单词(最大的数值)。

# Run this cell to answer the analogy -- man : king :: woman : x
pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'king'], negative=['man']))

这里women:king:: man:x
x为：

Question 2.4: Finding Analogies（寻找类比）

根据这些向量找到一个类比的例子(例如，想要的单词排在最前面)。在你的解决方案中，请以x:y:: a:b的形式陈述完整的类比。如果你认为这个类比很复杂，用一两个句子解释为什么这个类比是成立的

# ------------------
# Write your analogy exploration code here.

pprint.pprint(wv_from_bin.most_similar(positive=['China','beijing'], negative=['American']))

# ------------------

Question 2.5: Incorrect Analogy （错误的类比）

根据这些向量找到一个不成立的类比的例子

# ------------------
# Write your incorrect analogy exploration code here.

pprint.pprint(wv_from_bin.most_similar(positive=['China','American'], negative=['Japan']))

# ------------------

Question 2.6: Guided Analysis of Bias in Word Vectors（引导词向量偏差分析）

重要的是要认识到我们的单词嵌入隐含的偏见(性别、种族、性取向等)。

运行下面的单元格，检查
(a)哪些词与“woman”和“boss”最相似，而与“man”最不相似;
(b)哪些词与“man”和“boss”最相似，而与“woman”最不相似。
你在前10名中发现了什么?

# Run this cell
# Here `positive` indicates the list of words to be similar to and `negative` indicates the list of words to be
# most dissimilar from.
#这里“positive”表示类似的单词列表，而“negative”表示是最不相似于。
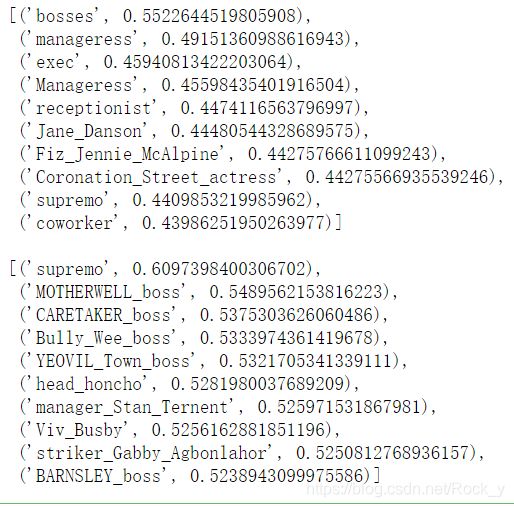
pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'boss'], negative=['man']))
print()
pprint.pprint(wv_from_bin.most_similar(positive=['man', 'boss'], negative=['woman']))

Question 2.7: Independent Analysis of Bias in Word Vectors （独立的单词向量偏差分析）

使用“most_similar”函数找到另一种情况，其中一些偏差显示的向量。请简要解释你发现的偏见的例子。

# ------------------
# Write your bias exploration code here.

pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'doctor'], negative=['man']))
print()
pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'nurse'], negative=['man']))

# ------------------

Question 2.8: Thinking About Bias [written]

是什么导致了向量这个词的偏差呢?

• 取决于训练集本身
• 数据量不足

参考

https://blog.csdn.net/Forlogen/article/details/93341527
https://blog.csdn.net/weixin_42691585/article/details/107154134