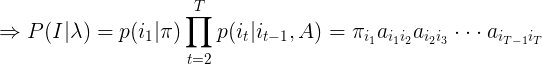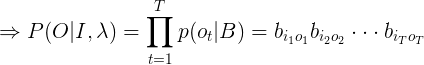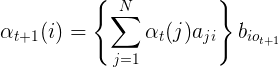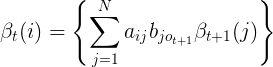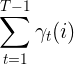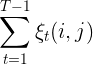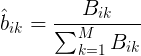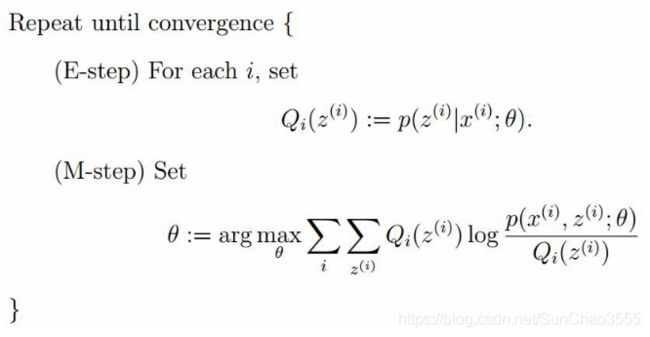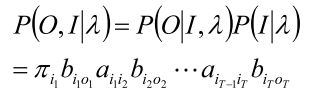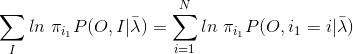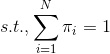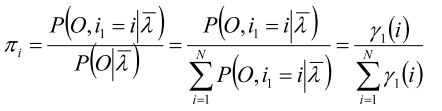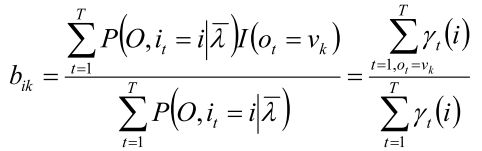HMM(Hidden Markov Model)
目录
HMM定义
HMM的确定
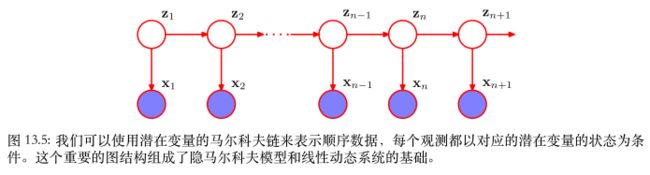
从⽣成式的观点考虑隐马尔科夫模型,我们可以更好地理解隐马尔科夫模型。
HMM的参数
统一定义:
HMM举例
HMM的3个基本问题
概率计算问题
定义:前向概率-后向概率
前向算法
后向算法
前后向关系
单个状态的概率:
两个状态的联合概率
期望
学习问题
监督学习方法
Baum-Welch算法(非监督学习方法)
预测问题
近似算法
Viterbi算法
python实现中文分词
-------七月算法机器学习笔记
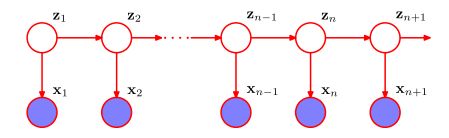
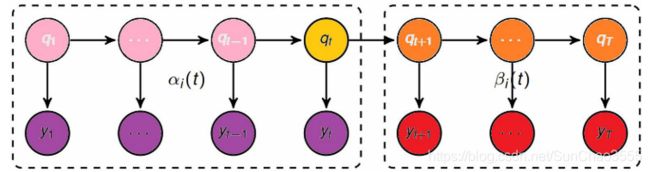
HMM定义
上图为HMM的贝叶斯网络,【![]() 不可观察的前提下,
不可观察的前提下,![]() 都不独立,不满足条件独立判定条件(tail-to-tail)】
都不独立,不满足条件独立判定条件(tail-to-tail)】
隐马尔科夫模型(HMM, Hidden Markov Model)可用于标注问题,在语音识别、NLP、生物信息、模式识别等领域被实践证明是有效的算法。
HMM是关于“时序”的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测,而产生观测随机序列的过程。
HMM随机生成的状态的序列,称为状态序列;每个状态生成一个观测,由此产生的观测随机序列,称为观测序列
--序列的每个位置可看做是一个时刻。
HMM的确定
根据马尔可夫随机过程,我们现在让潜在变量![]() 的概率分布
的概率分布![]() 对前一个潜在变量
对前一个潜在变量![]() 产生依赖。由于潜在变量是K维二值变量,因此条件概率分布对应于数字组成的表格,记做A,它的元素被称为转移概率。元素
产生依赖。由于潜在变量是K维二值变量,因此条件概率分布对应于数字组成的表格,记做A,它的元素被称为转移概率。元素![]() .由于它们是概率值,因此满足
.由于它们是概率值,因此满足![]() ,即行和为1.
,即行和为1.
直观意思是第n-1个时间步处于状态j时,那么在第n个时间步处于状态k的概率,(即下一个时间步,状态从j转移到k的概率)
从而矩阵A由K(K-1)个独立的参数。可以显式地将条件概率分布写成
初始潜在结点
很特别,因为它没有父结点,因此它的边缘概率分布
由一个概率向量
表示,元素为
即
,
(2)
可以通过定义观测变量的条件概率分布
来确定一个概率模型,其中B是控制概率分布的参数集合。这些条件概率被称为发射概率。因此对于一个给定的B值,概率分布
由一个K维的向量组成,对应于二值向量
的K个可能状态。我们可以将发射概率表示为,
从而观测变量和潜在变量上的联合概率分布为,
其中
表示控制模型参数的集合。
从⽣成式的观点考虑隐马尔科夫模型,我们可以更好地理解隐马尔科夫模型。
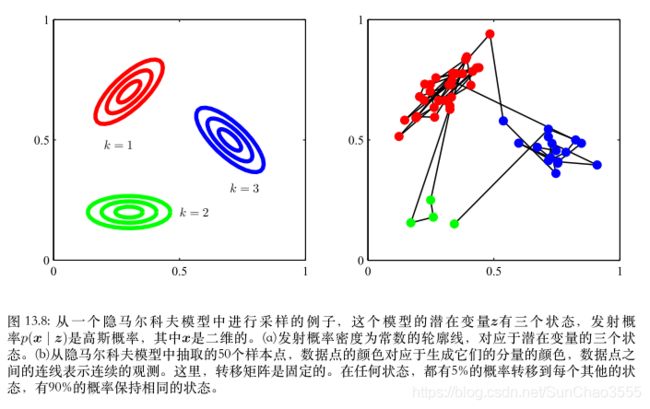
【马尔科夫模型为了从⼀个混合⾼斯分布中⽣成样本,我们⾸先随机算侧⼀个分量,选择的概率为混合系数πk, 然后从对应的⾼斯分量中⽣成⼀个样本向量x。这个过程重复N次,产⽣N个独⽴样本组成的数据集。
在【隐马尔科夫模型】的情形,这个步骤修改如下。⾸先我们选择初始的潜在变量z1,概率由参数πk控制,然后采样对应的观测x1。现在我们使⽤已经初始化的z1的值,根据转移概 率p(z2 | z1)来选择变量z2的状态。从⽽我们以概率Ajk选择z2的状态k,其中k = 1, . . . ,K。⼀ 旦我们知道了z2,我们就可以对x2采样,从⽽也可以对下⼀个潜在变量z3采样,以此类推。
这是有向图模型的祖先采样的⼀个例⼦。例如,如果我们有⼀个模型,其中对⾓转移元素Akk⽐ ⾮对⾓的元素⼤得多,那么⼀个典型的数据序列中,会有连续很长的⼀系列点由同⼀个概率分布⽣成,⽽从⼀个分量转移到另⼀个分量不会经常发⽣。图13.8说明了从隐马尔科夫模型⽣成样本的过程。
HMM的参数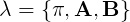
统一定义:
Q是所有可能的状态的集合----N是可能的状态数(等价于前面说的K维)
V是所有可能的观测的集合----M是可能的观测数(等价于观测值x的维度)
是长度为T的状态序列,O是对应的观测序列
A:状态转移概率矩阵
,
即在时刻t处于状态
的条件下时刻t+1转移到状态
的概率
B:观测(发射)概率矩阵
,
, 即在时刻t处于状态
的条件下生成观测
的概 率。
是初始状态概率向量
,
, 即 时刻t=1处于状态
的概率
HMM举例
该示例的各个参数
那么,在给定参数π、A、B的前提下,得到观测序列“红红白白红”的概率是多少?即
。 由此引出HMM的3个基本问题
HMM的3个基本问题
1)概率计算问题:前向-后向算法——动态规划
给定模型
和观测序列,计算模型λ下观测序列
出现的概率
2)学习问题:Baum-Welch算法(状态未知)——EM
已知观测序列
,估计模型
的参数,使得在该模型下观测序列
最大
3)预测问题:Viterbi算法——动态规划
解码问题:已知模型
和观测序列
求给定观测序列条件概率
最大的状态序列
概率计算问题
直接计算法:暴力算法
由公式(1)(2)
表示只与状态转移概率矩阵A和初始概率分布π有关
由公式(3)
表示只与观测(发射)概率矩阵B有关
由公式(4)![]() 和
和![]() 同时出现的联合概率:
同时出现的联合概率:
(7)
因此,对公式(7)中的所有可能的状态序列![]() 求和,即可得到
求和,即可得到![]() ,即
,即
对(8)式进行分析:加和符号中共有2T个因子,![]() 的遍历个数为
的遍历个数为![]() ,因此,时间复杂度为
,因此,时间复杂度为![]() ,指数级增长,复杂度过高。
,指数级增长,复杂度过高。
借鉴动态规划的方法,选择一个状态推算出它的状态转移方程。
chow-liu tree
【凡是树状或者链状(类树)的图,将任何一个节点作为某一时刻状态值,能够看到的输出就是它的前向;以它作为条件能够看到的输出就是它的后向】
思考:用贝叶斯网络的这套思维体系去影响深度学习的网络,从而将深度网络精简。
定义:前向概率-后向概率
这里y等价于(前面提到的)o;q即i
前向概率:
![]() , 表示第t个时刻位于第i号状态并且观察到了前t个观测值的概率;
, 表示第t个时刻位于第i号状态并且观察到了前t个观测值的概率;
或者说,前t个观测和第t个时刻位于状态i的联合概率
后向概率:
![]() ,表示在第t个时刻位于第i号状态时,能够观察到t+1及其后面的观测的概率
,表示在第t个时刻位于第i号状态时,能够观察到t+1及其后面的观测的概率
前向算法
定义:给定![]() ,到t时刻部分观测序列为
,到t时刻部分观测序列为![]() 且状态为
且状态为![]() 的概率称为前向概率
的概率称为前向概率
记做:![]()
可以递归计算前向概率![]() 及观测序列概率
及观测序列概率![]()
初值:
, (9)
即在时刻t=1时位于状态i且观察到了
的概率
递归:对于t=1,2…T-1
t+1时刻位于状态i的概率:t时刻的状态
转移到 t+1 时刻状态 i 的概率的和
----表示到达了t+1时刻的状态 i【我们只关注t+1时刻的状态,所以不关心t时刻的状态j,所以积分消去j】<类似全概率公式,加和规则,下面(11)同理>
那么,
即 (t+1时刻位于状态i的概率)且(观测到
)的概率
最终:我们得到
【T时刻位于状态i时,已经观测到整个序列O的概率】,将i积分掉,即得给定参数
,观测到序列O的概率
分析时间复杂度:
(11)![]() (10)
(10)
后向算法
![]() ,表示在第t个时刻位于第i号状态时,能够观察到t+1及其后面的观测的概率
,表示在第t个时刻位于第i号状态时,能够观察到t+1及其后面的观测的概率
初值:
, (12)
在最后时刻T,已经不需要(没有)后面的观测,存在即为1
递推:对于t=T-1,T-2,...,1
保证t+1时刻已经观测到序列
的前提下(即
),
还要求t时刻状态i能够转移到下一个时刻t+1的某一个状态且能够观测到
【t时刻状态i转移到t+1时刻的任一状态时,只要能观测到
即可保证
能够观测到序列
,
因此与j无关,积分消掉】
最终:当递归到最后一步t=1时,还有
未观测到,因此同理
前后向关系
根据定义,公式(7):
( 15 )
单个状态的概率:
给定模型λ和观测O,在时刻t处于状态![]() 的概率。 记,
的概率。 记,
![]() (16)
(16)
结合公式(15)以及前后向概率的定义,化简得
![]() 的意义:
的意义:
在每个时刻t选择在该时刻最有可能出现的状态![]() ,从而得到一个状态序列
,从而得到一个状态序列![]() ,将它作为预测的结果。
,将它作为预测的结果。
两个状态的联合概率
求给定模型λ和观测O,在时刻t处于状态![]() 并且时刻t+1处于状态
并且时刻t+1处于状态![]() 的概率。
的概率。
(18)
而
(19)
期望
学习问题
1)若训练数据包括观测序列和状态序列,则HMM的学习非常简单,是监督学习;
2)若训练数据只有观测序列,则HMM的学习需要使用EM算法,是非监督学习。
监督学习方法
假设已给定训练数据包含S个长度相同的观测序列和对应的状态序列![]() ,那么,可以直接利用Bernoulli大数定理的结论“频率的极限是概率”,给出HMM的参数估计。
,那么,可以直接利用Bernoulli大数定理的结论“频率的极限是概率”,给出HMM的参数估计。
转移概率
的估计:
设样本中时刻t处于状态i时刻t+1转移到状态j的频数为
,则
观测概率
的估计:
设样本中状态i并观测为k的频数为
,则
初始状态概率
的估计为S个样本中初始状态为
的概率。
Baum-Welch算法(非监督学习方法)
EM算法整体框架
EM过程:对数似然
所有观测数据写成
,所有隐数据写成
,完全数据是
, 完全数据的对数似然函数是
假设
是HMM参数的当前估计值,
为待求参数。
( 20 )
根据公式(7)
函数可写成:
(21)
极大化Q,求得参数A,B,π
由于该三个参数分别位于三个项中【公式(21)】,可分别极大化
第一项:π
利用lagrange乘子法,得:
对
求偏导,并等0,得
(25)
将公式(25)回带到(24)得
第二项:转移概率
仍然使用Lagrange乘子法,得
第三项:观测(发射)概率
同理,得
预测问题
近似算法
Viterbi算法
近似算法
Viterbi算法
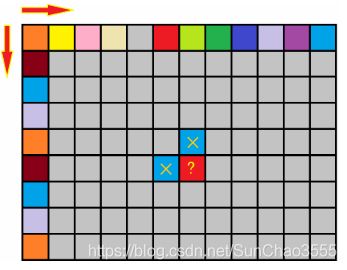
思考:算法(走棋盘/格子取数)
给定m*n的矩阵,每个位置是一个非负整数,从左上角开始,每次只能朝右和下走, 走到右下角,求总和最小的路径。
动态规划状态转移方程:
走的方向决定了同一个格 子不会经过两次。
若当前位于(x,y)处,它来自于哪些格子呢?
dp[0,0]=a[0,0] / 第一行(列)累积
dp[x,y] = min(dp[x-1,y]+a[x,y],dp[x,y-1]+a[x,y])
即:dp[x,y] = min(dp[x-1,y],dp[x,y-1]) +a[x,y]
思考:若将上述问题改成“求从左上到右下的最大路径”呢?
Viterbi算法实际是用动态规划解HMM预测问题,用DP求概率最大的路径(最优路径), 这条路径对应一个状态序列。
定义变量![]() :在时刻t状态为i的所有路径中,概率的最大值。
:在时刻t状态为i的所有路径中,概率的最大值。
与前向算法过程类似
定义:
递推:
终止:
python实现中文分词
训练集和测试集均使用开源数据集:http://sighan.cs.uchicago.edu/bakeoff2005/
参考了博客:https://blog.csdn.net/aaalswaaa1/article/details/83745785
参数学习使用了监督学习
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pylab
from pandas import DataFrame, Series
import os
plt.rcParams['font.sans-serif'] = ['SimHei'] #指定默认字体
plt.rcParams['axes.unicode_minus'] = False #解决保存图像是负号'-'显示为方块的问题
import pickle
class HMM(object):
def __init__(self):
self.state_list=[0,1,2,3]#['B','M','E','S']
self.words=set()
self.count=np.zeros((4,1))
self.model_file = 'datasets/hmm_model2.pkl'
def load_model(self,trained=True):
if trained:
with open(self.model_file,'rb') as f:
self.A=pickle.load(f)
self.B=pickle.load(f)
self.pi=pickle.load(f)
self.load_parameter=True
f.close()
else:
self.A = np.zeros((4, 4))
self.B = np.ones((4, 65536))
self.pi = np.zeros((4, 1))
self.load_parameter=False
def markLabel(self,text):
out_text=[]
if len(text)==1:
out_text.append(3)
else:
out_text+=[0]+[1]*(len(text)-2)+[2]
return out_text
def train(self,path):
self.load_model(False)
line_num=-1
#'datasets/pku_training.txt'
with open(path) as f:
for line in f:
line_num+=1
line=line.strip()
# print(line)
if not line:
continue
# if line_num==10:
# break
word_list=[i for i in line if i !=' ']
# print(word_list)
self.words |=set(word_list)
line_list = line.split()
# print(line_list)
O_state=[]
for w in line_list:
O_state.extend(self.markLabel(w))
# print(line)
print(O_state)
# print(word_list)
for k,v in enumerate(O_state):
self.count[v]+=1
if k==0:
self.pi[v,0]+=1
else:
self.A[O_state[k-1],v]+=1
self.B[v,ord(word_list[k])]+=1
# print(word_list[k])
f.close()
self.pi/=line_num
self.A/=(np.sum(self.A,axis=1).reshape(4,1))
print(self.A)
self.B/=np.sum(self.B,axis=1).reshape(4,1)
print(self.B)
with open(self.model_file,'wb') as f:
pickle.dump(self.A,f)
pickle.dump(self.B,f)
pickle.dump(self.pi,f)
f.close()
def viterbi(self, pi, A, B, o):
T = len(o) # 观测序列
delta = [[0 for i in range(4)] for t in range(T)]
pre = [[0 for i in range(4)] for t in range(T)] # 记录前一个状态
for i in range(4):
delta[0][i] = pi[i,0]*B[i,ord(o[0])]
for t in range(1, T):
for i in range(4):
delta[t][i] = delta[t - 1][0]*A[0,i]
for j in range(1, 4):
vj = delta[t - 1][j]*A[j,i]
if delta[t][i] < vj:
delta[t][i] = vj
pre[t][i] = j
delta[t][i] *= B[i,ord(o[t])]
decode = [-1 for t in range(T)] # 解码:回溯查找最大路径
q = 0
for i in range(1, 4):
if delta[T - 1][i] > delta[T - 1][q]:
q = i
decode[T - 1] = q
for t in range(T - 2, -1, -1):
q = pre[t + 1][q]
decode[t] = q
return decode
def segment(self,sentence,decode):
'''
B:一个词的开始
E:一个词的结束
M:一个词的中间
S:单字成词
举例:你S现B在E应B该E去S幼B儿M园E了S
'''
print(decode)
N=len(sentence)
i=0
while i非监督学习参数(未完)
def log_sum(self,array):
t=0
for i in range(len(array)):
t+=array[i]
return t
def cal_alpha(self,pi,A,B,o,alpha):
for i in range(4):
alpha[0][i]=pi[i]+B[i][ord(o[0])]
T=len(o)
temp=[0 for k in range(4)]
for t in range(1,T):
for i in range(4):
for j in range(4):
temp[j]=(alpha[t-1][j]+A[j][i])
alpha[t][i]=self.log_sum(temp)
alpha[t][i]+=B[i][ord(o[t])]
return alpha
def cal_beta(self,pi,A,B,o,beta):
T=len(o)
for i in range(4):
beta[T-1][i]=1
temp=[0 for k in range(4)]
for t in range(T-2,-1,-1):
for i in range(4):
beta[t][i]=0
for j in range(4):
temp[j]=A[i][j]+B[j][ord(o[t+1])]+beta[t+1][j]
beta[t][i]+=self.log_sum(temp)
return beta
def cal_gamma(self,alpha,beta,gamma):
for t in range(len(alpha)):
for i in range(4):
gamma[t][i]=alpha[t][i]+beta[t][i]
s=self.log_sum(gamma[t])
for j in range(4):
gamma[t][j]-=s
return gamma
def cal_xi(self,alpha,beta,A,B,o,xi):
T=len(alpha)
temp=[0 for x in range(16)]
for t in range(T-1):
k=0
for i in range(4):
for j in range(4):
xi[t][i][j]=alpha[t][i]+A[i][j]+B[j][ord(o[t+1])]+beta[t+1][j]
temp[k]=xi[t][i][j]
k+=1
s=self.log_sum(temp)
for i in range(4):
for j in range(4):
xi[t][i][j]-=s
return xi
def bw(self,pi,A,B,alpha,beta,gamma,xi,o):
T=len(alpha)
for i in range(4):
pi[i]=gamma[0][i] #π
s1=[0 for x in range(T-1)]
s2=[0 for x in range(T-1)]
for i in range(4):
for j in range(4):
for t in range(T-1):
s1[t]=xi[t][i][j]
s2[t]=gamma[t][i]
A[i][j]=self.log_sum(s1)-self.log_sum(s2)#A
s1=[0 for x in range(T)]
s2=[0 for x in range(T)]
for i in range(4):
for k in range(65536):
valid=0
for t in range(T):
if ord(o[t])==k:
s1[valid]=gamma[t][i]
valid+=1
s2[t]=gamma[t][i]
if valid==0:
B[i][k]=-3.14e+100
else:
print('**********')
B[i][k]=self.log_sum(s1[:valid])-self.log_sum(s2)#B
return A,B,pi
def baum_welch(self,pi,A,B):
df = pd.read_excel('datasets/meituan.xls', usecols=['comment'])
df = df.dropna()
preprocessed = set(df['comment'])
df2 = DataFrame(preprocessed, columns=['comment'])
# df=pd.read_excel('datasets/meituan1.xls')
sentence=df2.ix[2,0]
print(sentence)
# sentence=list(df2['comment'])
T=len(sentence)
print(T)
alpha=[[0 for i in range(4)] for t in range(T)]
beta=[[0 for i in range(4)] for t in range(T)]
gamma=[[0 for i in range(4)] for t in range(T)]
xi=[[[0 for j in range(4)] for i in range(4)] for t in range(T-1)]
for time in range(100):
print(B)
alpha=self.cal_alpha(pi,A,B,sentence,alpha)
beta=self.cal_beta(pi,A,B,sentence,beta)
gamma=self.cal_gamma(alpha,beta,gamma)
xi=self.cal_xi(alpha,beta,A,B,sentence,xi)
A,B,pi=self.bw(pi,A,B,alpha,beta,gamma,xi,sentence)
# print(A,B,pi)
decode=self.viterbi(pi, A, B, df2.ix[4,0])
self.segment(df2.ix[4,0],decode)
return pi,A,B
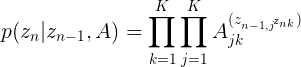
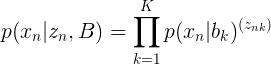
![\large p(X,Z|\lambda)=p(z_1|\pi)\left [ \prod_{n=2}^Np(z_n|z_{n-1},A) \right ]\prod_{m=1}^Mp(x_m|z_m,B)](http://img.e-com-net.com/image/info8/03edf0b5de744cf8bfdf7dbe20591d14.gif)