第九次模拟测试-3
题目描述 在瑞神大战宇宙射线中我们了解到了宇宙狗的厉害之处,虽然宇宙狗凶神恶煞,但是宇宙狗有一 个很可爱的女朋友。
最近,他的女朋友得到了一些数,同时,她还很喜欢树,所以她打算把得到的数拼成一颗树。
这一天,她快拼完了,同时她和好友相约假期出去玩。贪吃的宇宙狗不小心把树的树枝都吃掉 了。所以恐惧包围了宇宙狗,他现在要恢复整棵树,但是它只知道这棵树是一颗二叉搜索树,同 时任意树边相连的两个节点的gcd(greatest common divisor)都超过1。
但是宇宙狗只会发射宇宙射线,他来请求你的帮助,问你能否帮他解决这个问题。
补充知识:
GCD:最大公约数,两个或多个整数共有约数中最大的一个 ,例如8和6的最大公约数是2。
一个简短的用辗转相除法求gcd的例子:
int gcd(int a,int b)
{
return b == 0 ? a : gcd(b,a%b);
}
输入描述 输入第一行一个t,表示数据组数。
对于每组数据,第一行输入一个n,表示数的个数
接下来一行有n个数 a i a_i ai,输入保证是升序的。 输出描述 每组数据输出一行,如果能够造出来满足题目描述的树,输出Yes,否则输出No。
无行末空格。 样例输入1
1 6 3 6 9 18 36 108
样例输出1
Yes
样例输入2
2 2 7 17 9 4 8 10 12 15 18 33 44 81
样例输出2
No Yes
样例解释 样例1可构造如下图
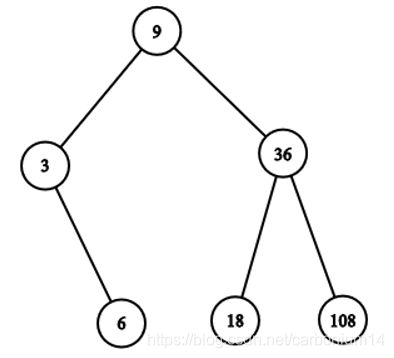
数据组成 给出的数为上限。
数据点数 t n a i a_i ai 1,2,3 5 15 1 0 9 10^9 109 4,5,6 5 35 1 0 9 10^9 109 7,8,9,10 5 700 1 0 9 10^9 109
题目分析:
本题可以用暴力解决,但是遇到四个点的时候就发现解决不了了,于是一分也没拿到QAQ。后来想了想这里实际上是一个动态规划问题,由于这是一个二叉搜索树,这样意味着他是有序的,也就是对于合适的数,看看他的两边的数是不是符合要求,如果符合要求了,那就把范围缩小到符合要求的范围当中,一直递归直到所有的点都符合那就符合要求,如果遇到了一个点不符合要求(比他小的比他大的都不能构成相邻的孩子)那就意味着不符合要求了。
不过如果仅仅这中递归会导致时间复杂度非常的高,因为重复操作太多了,所以我们把它分开,维护四个数组,两个是判断操作有没有进行过,两个是判断是不是可行,l意味着从左孩子到自己,r意味着从自己到右孩子。
bool al[710][710];
bool ar[710][710];
bool cl[710][710];
bool cr[710][710]
然后就可以开始检测了,如果发现对应范围内的数组都已经检测过了,就看他的结果是不是满足要求。(这里要注意你的范围是闭区间,所以要++表示是下一个的开头)
if(al[l+1][n+1]==true&&ar[n+1][r+1]==true)
{
if(cl[l+1][n+1]==true&&cr[n+1][r+1]==true)
{
return true;
}
else
{
return false;
}
}
当然了,如果递归到后来发现左孩子或者右孩子和自己重合了,那也意味着成功了,因为这样就意味着不断的递归过程中都满足要求(否则就不敌跪了,直接返回false),所以是符合要求了。
if(l>=n-1&&r<=n+1)
{
return true;
}
如果发现还没有经历过,那就对中间的每一个gcd都大于1的点进行遍历,如果符合要求了或者发现左右孩子和自己重合了(原因见上)就符合要求,然后更新数组,记录状态。右边和左边是一样的,只不过是符号不用而已
if(al[l+1][n+1]==false)
{
bool judgel=false;
if(l==n-1)
{
judgel=true;
}
for(int u=l+1;u<n;u++)
{
if(gcda[u][n]>1)
{
if(try_(l,u,n)==true)
{
judgel=true;
}
}
}
al[l+1][n+1]=true;
cl[l+1][n+1]=judgel;
}
if(ar[n+1][r+1]==false)
{
bool judger=false;
if(r==n+1)
{
judger=true;
}
for(int u=n+1;u<r;u++)
{
if(gcda[n][u]>1)
{
if(try_(n,u,r)==true)
{
judger=true;
}
}
}
ar[n+1][r+1]=true;
cr[n+1][r+1]=judger;
}
然后就可以进行判断是不是符合要求了。
if(cl[l+1][n+1]==true&&cr[n+1][r+1]==true)
{
return true;
}
else
{
return false;
}
这样我们首先输入他们的gcd,当然gcd运算是可交换的,所以对于存储而言我们可以扫描半边,然后另一半通过手动来加入。
for(int i=0;i<n;i++)
{
for(int j=i;j<n;j++)
{
gcda[i][j]=gcd(a[i],a[j]);
gcda[j][i]=gcda[i][j];
}
}
之后对着0到n-1的范围扫描每一个数是不是符合要求就可以了。
bool judge=false;
for(int i=0;i<n;i++)
{
if(try_(-1,i,n)==true)
{
judge=true;
break;
}
}
当然了,他要求的是不能有多余的行,那么我们在非最后一行就输出换行,其余的不输出换行。
if(t!=temp-1)
{
cout<<endl;
}
代码如下:
#include