精度、召回率、准确率、F1、ROC、AUC的理解
1. 错误率、精度
精度(accuracy) 分类正确的样本数占总样本数的比例
错误率(error rate) 分类错误的样本数占总样本数的比例
通常来说精度(accuracy)不是一个好的性能指标,尤其是处理数据有偏差时候比如一类非常多,一类很少
比如手写数字识别问题,只判断一副图片是不是5,由于5的图片只占百分之10左右,所以分类器总是预测图片不是5都会有90%左右的可能性是对的
2. 混淆矩阵、准确率、召回率、F1
为了更好的度量性能所以引入准确率、召回率等概念。
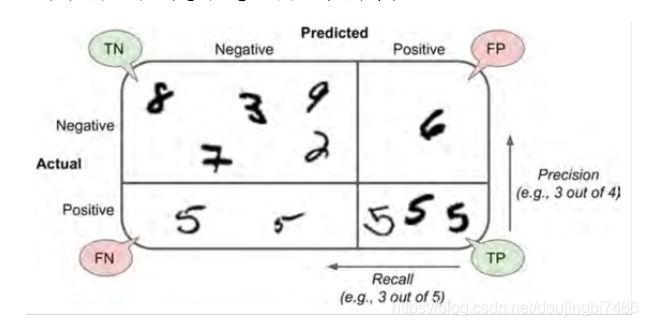
混淆矩阵 每一行代表实际的类,每一列代表预测的类
| 预测为正 | 预测为反 | |
|---|---|---|
| 实际为正 | true positive | false negative |
| 实际为反 | false positive | true negative |
其格式为 [预测正确性,预测结果]
准确率(precision):及正例预测的精度 p r e c i s i o n = T P T P + F P precision = \frac{TP}{TP + FP} precision=TP+FPTP, 查的准确的程度
召回率(recall):也叫做敏感度,或者真正例率,这是正例被分类器正确探测出的比率 r e c a l l = T P T P + F N recall = \frac{TP}{TP + FN} recall=TP+FNTP 查全的程度
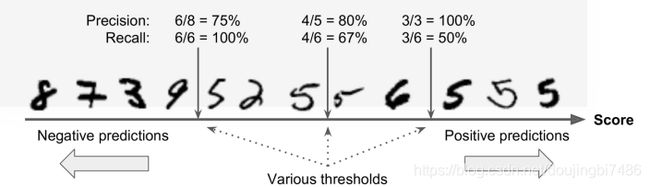
例如 precision = 0.7 那么说明分类器预测为正例的结果中,只有70%是真正的正例,是正确的,即对于一个预测为正例的结果,只有70%的可能性是正确的
recall = 0.7 时候说明分类器只能查出70%的正例
F 1 F_1 F1socre是召回率和准确率的结合,使两者的调和平均,所谓调和平均就是会给小的值更大的权重,而不是同等地位看待,所以若要F1值高,那么需要两者都高.
F 1 = 2 1 r e c a l l + 1 p r e c i s i o n = 2 ∗ p r e c i s i o n ∗ r e c a l l r e c a l l + p r e c i s i o n = T P T P + F N + F P 2 F1 = \frac{2}{\frac{1}{recall} + \frac{1}{precision}} = 2* \frac{precision*recall}{recall + precision} = \frac{TP}{TP + \frac{FN+FP}{2}} F1=recall1+precision12=2∗recall+precisionprecision∗recall=TP+2FN+FPTP
3. 准确率和召回率的折中
召回率和准确率不可兼得,增加准确率会降低召回率,增加召回率会降低准确率,因为保证准确率,那么将会对预测结果严格筛选,这将导致部分正例被筛选淘汰,导致召回率降低。保证召回率,那么就会降低筛选的门槛,尽可能多的将正例筛选出来,那么就会有一些反例被筛选进去,导致准确率下降。
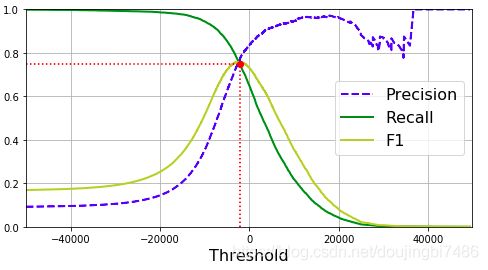
如图所示,随着阈值的提高,精确度不断上升,召回率不断下降,阈值下降,那么精准度不断下降,召回率不断上升。
注意:阈值的提升不见得准确率一定会提升,会出现抖动的情况,只取决于淘汰正例以及反例的数量多少关系
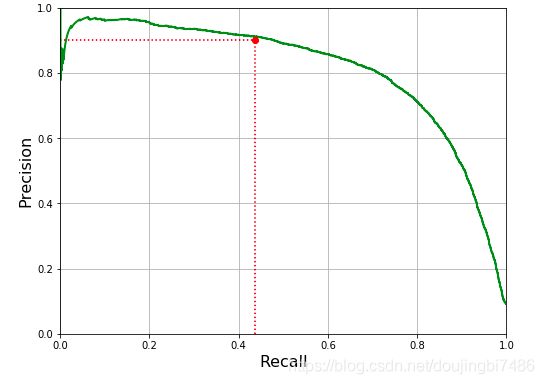
也可以通过直接画出召回率对准确率的曲线来进行观察,在其急剧下降之前根据需求选择合适点
4. ROC 曲线
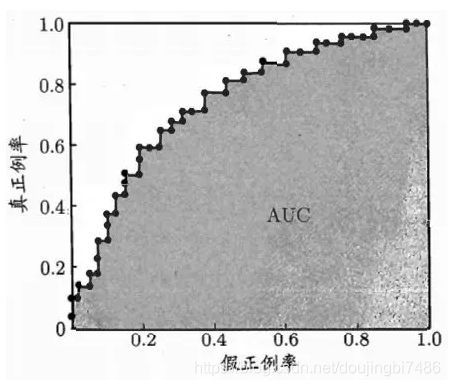
ROC 曲线是从阈值选取角度出发来研究学习器泛化性能的工具,可以通过ROC曲线来比较不同分类器的性能。ROC 曲线是召回率(TPR)对假正例率(FPR)的曲线(FPR 是反例被错误分成正例的比率),其横轴为FPR,纵轴为TPR。
其中 FPR = 1 - TNR ,TNR 为 真反例率反例被正确分类的比率,也叫作特异性。
其中召回率越高,那么假正例就越高。
ROC曲线绘制
现实中由于样例数量的限制,ROC曲线并非光滑的。
绘制过程:给定 m + m^+ m+正例和 m − m^- m−个反例,然后将模型预测的结果进行排序(从大到小)。首先降分类的阈值设置为最大,这样所有的样例都被预测为为反例,所以真正例率和假正例率都是0,即对应标记点(0,0)点。然后调整阈值,将阈值设置为每个样例的预测结果值,从而依次划分每个样例。设前一个标记点为(x,y),若当前样例为真正例,那么新的标记点为 ( x , y + 1 m + ) (x,y+\frac{1}{m^+}) (x,y+m+1),若为假正例,那么新的标记点为 ( x + 1 m + , y ) (x+\frac{1}{m^+},y) (x+m+1,y),然后依次操作下去直至遍历所有的样例,得到如下图。
AUC
对于两条ROC曲线若没有相交,那么左上角的曲线对应的学习器性能更好,但是若存在相交那么就难以判断,所以引入ROC的面积来作为评判依据。
ROC曲线下面的面积数值叫做AUC,利用数值可以直观的评价分类器好坏。好的分类器AUC值大,纯粹随机的分类器ROC为 0.5。
AUC 计算方法
假设ROC曲线对应的坐标分别为 { ( x 1 , y 1 ) , ( x 2 , y 2 ) ( x 3 , y 3 ) , . . . , ( x n , y n ) } \{(x_1,y_1),(x_2,y_2)(x_3,y_3),...,(x_n,y_n)\} {(x1,y1),(x2,y2)(x3,y3),...,(xn,yn)},那么AUC估算公式如下:
A U C = 1 2 ∑ i = 1 m − 1 ( x i + 1 − x i ) ∗ ( y i + 1 + y i ) AUC =\frac{1}{2} \sum_{i=1}^{m-1}{(x_{i+1} -x_{i})*(y_{i+1} + y_{i})} AUC=21i=1∑m−1(xi+1−xi)∗(yi+1+yi)
AUC 意义
AUC代表着预测为正例排在负例前面的概率。AUC就是从所有正样本中随机选择一个样本,从所有负样本中随机选择一个样本,然后利用学习器进行预测,正样本被预测为正的概率为 P 1 P_1 P1,负样本被预测为正的概率为 P 2 P_2 P2, P 1 > P 2 P_1 > P_2 P1>P2的概率被称为AUC
ROC和准确率/召回率曲线相似,当正例很少的时候采用准确率召回率曲线,其它情况使用ROC
5. 参考
- ROC曲线和AUC面积理解
https://blog.csdn.net/program_developer/article/details/79946787 - hands on machine learning with sk-learn and tf