时频分析:短时傅里叶变换(1)
目录:
文章目录
- 目录:
- 前言
- 1傅里叶变换的缺陷
- 2短时傅里叶变换(窗式傅里叶变换)
- 3小波部分
- 4补充部分
- 补充
前言
最近需要对处理的数据做时频分析,因此恶补了一下相关的知识,光是学习并没有用处,因此,总结了一下自己的学习经验,写下了这篇帖子,方便大家学习。
怕什么真理无穷,进一寸有一寸的欢喜 胡适
学以致用,以用促学。
1傅里叶变换的缺陷
先写完这个,再补一篇傅里叶分析。
FT在平稳信号的分析和处理中有着突出贡献的原因在于,人们利用它可以把复杂的时间信号和空间信号变换到频率域中,然后用相对简单的频谱特性去分析和发现原信号的动态特性。
FT 正变换告诉我们:从时间(空间)信号中提取信号的频谱信息 F ( W ) F(W) F(W),就是使用整个时间域的所有信息来计算单个确定频率的谱值(频域函数 F ( w ) F(w) F(w)的任一频率 w 0 w_0 w0对应的函数值),这是由时间轴 ( − ∞ , ∞ ) (-\infty ,\infty) (−∞,∞)上的确定信号 f ( t ) f(t) f(t)决定的。因此,它求出的频域函数对应的时整个时间轴,所以可以知道,傅里叶变换对频谱的描绘是“全局性”的,不能反映时间维度局部区域上的特征,人们虽然从傅立叶变换能清楚地看到一整段信号包含的每一个频率的分量值,但很难看出对应于频率域成分的不同时间信号的持续时间和发射的持续时间,缺少时间信息使得傅立叶分析再更精密的分析中失去作用。
伊利诺依斯大学教授曾说:“若你记录1小时长的信息而在最后5分钟出错,这一错误就会毁了整个傅立叶变换。相位的错误是灾难性的,如果在相位上哪怕犯了一个错误,你最后就会发现你所干的事与最初的信号无关了。”1
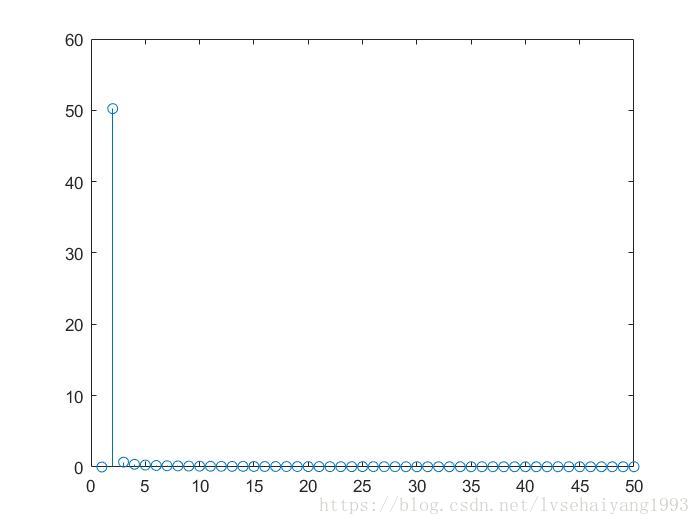
t=0:.01:5;
x=sin(2pit);
figure,plot(t)
y=fft(x(1:101));
figure,stem(abs(y(1:50)))
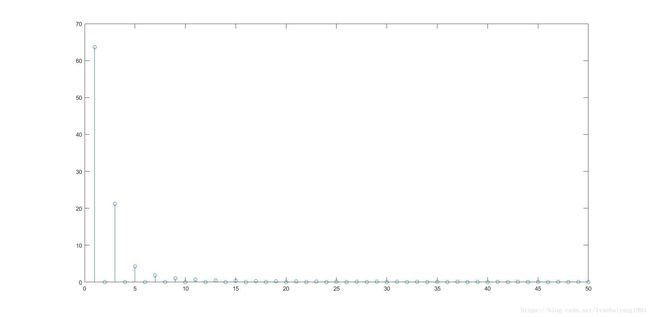
> x2=[x(1:50),x(1:50)];
> y2=fft(x2);
> figure,stem(abs(y2(1:50)))
而这个频谱图却很杂乱,但事实上这两个信号的主频应该是一样的,只是相位发生了跳变,因此,相位很关键。
2短时傅里叶变换(窗式傅里叶变换)
基本思想:局部平稳化-把长的非平稳随机过程看成是一系列短时随机平稳信号的叠加,短时性可通过在时间上加窗口函数实现(即截取一部分源数据)。通过该方法,人们至少可以说,无论发现了什么频率成分,它一定是发生在信号被截取的某个特定时间段内。
具体实现则是通过在傅立叶变换中,使用时间窗口函数 g ( t − u ) g(t-u) g(t−u)与源信号 f ( t ) f(t) f(t)相乘,实现在 u u u附近的加窗口和平移,然后进行傅立叶变换。在线性空间有一个可测的、平方可积的函数$f(t) \in L^2® $,对其进行短时傅立叶变换:
G f ( ϵ , u ) = ∫ f ( t ) g ( t − u ) e j ϵ t d t G_f(\epsilon,u)=\int f(t)g(t-u)e^{j\epsilon t}dt Gf(ϵ,u)=∫f(t)g(t−u)ejϵtdt
窗口傅立叶变换的逆变换式:
f ( t ) = 1 2 π A ∫ ∫ G f ( ω , u ) e − j ω t g ( t − u ) d ω d u f(t)=\frac{1}{2\pi A}\int \int G_f(\omega,u)e^{-j\omega t }g(t-u)d\omega du f(t)=2πA1∫∫Gf(ω,u)e−jωtg(t−u)dωdu
3小波部分
由短时傅立叶变换对函数(信号)进行的分析,相当于用一个形状、大小和放大倍数相同的“放大镜”在时-频域平面上移动去观察某固定长度时间内的频率特性。这里的问题是:尽管窗式傅立叶变换能解决变换函数的时域局域化问题,但是,其窗口的大小和形状是固定的,即窗口没有自适应性。这意味着什么?不能针对具体的问题进行优化。
而实际问题中,则各个要求“私人定制”,对于信息集中在高频的信号,由于波形相对较窄,时间间隔要小,采样频率要高,以求给出比较好的精度,进而更好地确定峰值,或者说需要用窄的时域窗来反映信息的高频成分;而对于低频谱信息,由于波形相对是宽的,时间段要相对的长才能给出完整的信号信息,或者说必须用较宽的时域窗来反映信息的低频成分。如果用固定的短时傅里叶变换,你选择一扇宽窗子,低频成分可以看得清楚,在高频部分确定时间时就很糟糕;若你选一扇窄窗子,在高频可以很好确定时间,但在低频的频率就可能装不进去。
这样,真正合适的做法是“放大镜”的长宽是可以变化的,正是为了实现这样的目的,人们引进了小波变换
4补充部分
短时傅里叶变换是最常用的一种时频分析方法,它通过时间窗内的一段信号来表示某一时刻的信号特征。在短时傅里叶变换过程中,窗的长度决定频谱图的时间分辨率和频率分辨率,窗长越长,截取的信号越长,信号越长,傅里叶变换后频率分辨率越高,时间分辨率越差;相反,窗长越短,截取的信号就越短,频率分辨率越差,时间分辨率越好,也就是说短时傅里叶变换中,时间分辨率和频率分辨率之间两者不可兼得,必须根据具体需求进行取舍。
简单来说,短时傅里叶变换就是先把一个函数和窗函数进行相乘,然后再进行一维的傅里叶变换。并通过窗函数的滑动得到一系列的频谱函数,将这些结果依次开便得到一个二维的时频图。
短时傅里叶变换的公式为
S T F T z = ∫ − ∞ + ∞ [ z ( u ) g ( u − t ) ] e − j 2 π f u d u STFT_z=\int_{-\infty} ^{+\infty} [z(u)g(u-t)]e^{-j2\pi fu}du STFTz=∫−∞+∞[z(u)g(u−t)]e−j2πfudu
其中Z(u)为源信号,g(u-t )为窗函数。
补充
如果还是有不会的,可以扫码关注这个公众号:博主会在24小时内回复

参考:
小波与短时
spectrogram函数
短时傅里叶变换
发言稿
这话该如何理解呢?
举个显示的例子,对于一个信号,
`b ↩︎