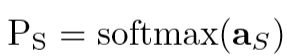FITNETS: Hints For Thin Deep Nets论文初读
目录
摘要
引言
方法
KD的回顾
提出基于Hint的训练方式(应该就是CL)
与CL训练的关系
实验结果(挑选的有意思的)
实验分析
结论
摘要
不仅仅用到了输出,还用到了中间层作为监督信息
让学生网络变得更深的同时,让它变的更快
引言
- 之前蒸馏的做法:
之前一篇论文是用集成的模型作为老师模型,来得到一个更宽但更浅的网络;
另一篇论文是将老师模型的输出的软标签作为监督信息,来得到一个相同深度的网络
- 深层次网络有好处的证据:
相对于浅层信息,深度信息是呈指数形式地有表达能力;
sota都是深层的(19,22层)
- Curriculum Learning strategies有好处的原因:
使得模型一层一层低接受更难的问题,而不是直接接受最难的问题;
加速收敛,在一个非凸问题上找到更好的局部最小值
- 本文的目的:
利用网络深度的优势和CL训练的优势,从宽深网络出发训练出一个窄但更深网络
方法
KD的回顾
- 损失函数
H表示交叉熵损失函数,小写的弯曲T表示一个soften因子
- 损失函数的分析
第一部分是常规的交叉熵;
第二部分是为了引入除了概率最高的类别以外的其他类别的相对相似性的更多信息
在T非常小的情况下,梯度会接近于pi-qi,所以当多个类别的qi接近于0时,最终输出的相似性信息是没有体现在梯度中的,所以网络会忽略掉这些信息;当T非常大的情况下,梯度会接近li-zi,这时的梯度是logits之间的差,就算最终的概率值都很小的情况下,由于logits的值并不小,而且logits之间也是有明显区别的,所以也会将概率接近于0的类别的相似性信息考虑到
提出基于Hint的训练方式(应该就是CL)
- 损失函数
其中:
uh代表teacher网络中的第一层到hint层的函数映射,Whint表示其中的参数;
vg代表student网络中的第一层到hidden层的函数映射,Wguided表示其中的参数;
r代表hidden层的一个额外的映射关系,Wr是其中的参数,这是为了使得hidden层与hint层的神经元大小一致
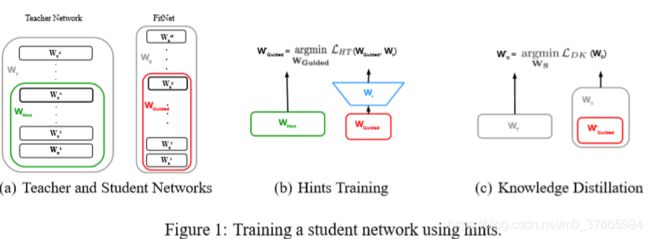
- Fitnet的分阶段训练
用很小的随机值初始化Wr
通过HT损失训练Wguided(Figure 1(b))
通过KD损失训练Ws(Figure 1 (c))
与CL训练的关系
退化在KD损失中的lamda参数,使得在第二阶段训练的时候先着重训练简单样本,然后再降低简单样本的权重,这与CL的训练方式一样,只不过省掉了针对任务手动设计的先验信息。
实验结果(挑选的有意思的)
- 对比试验-关于用desired output代替hint的实验
分阶段训练,第一阶段用交叉熵代替HT,第二阶段不变,结果失败;
分阶段训练,第一阶段用KD代替HT,第二阶段不变,结果失败;
联合训练,第一阶段不变(HT),第二阶段用交叉熵;结果失败;
联合训练,第一阶段不变(HT),第二阶段用KD,结果失败;
前两个实验说明了HT损失的重要性,不能被KD或者交叉熵代替的原因可能是KD或者交叉熵中的输出代表的是预测目标的类别信息,而要得到这个信息,需要网络得到一个较深语义的信息,这种特征需要比较深的层数才能提取到,而在网络的中间是提取不到的;
后两个实验说明了分段训练的重要性,原因,不知道,待补充。。。
不重要,待补充。。。。。
实验分析
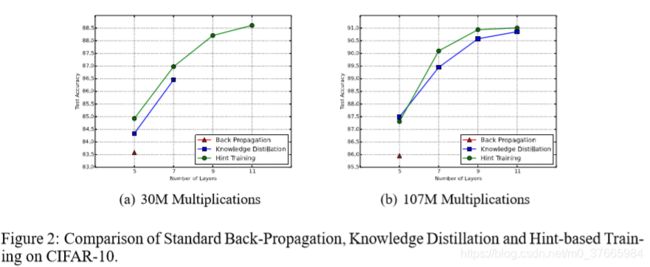
- 实验结果
相比于用KD和普通交叉熵,用HT更容易训练一个深的网络
在相同的计算量的情况下,更深的网络具有更好的性能
- 重要的分析
KD与HT都相当于一种正则化,而HT的正则化效果要好与KD
- 关于正则化的感悟
正则化相当于不要让网络去自己仅仅根据自己的经验学一些不普适的规则,而要干预网络,帮助它学习一些好的泛化规则
KD在损失中加入了teacher的经验,包含了除最大概率类别外的其他类别的分布信息,帮助网络学习较好的泛化规则
HT在KD的基础上,加入了hint损失,干预了网络对浅层单元的自我学习,帮助student网络学习好的特征
结论
用hint作为监督信息训练中间层要好于target
深层网络的性能能达到甚至超过10倍参数于它的浅层网络的性能