Meanshift算法学习笔记

Meanshift算法实际是一个自适应的梯度上升搜索峰值的算法

首先介绍两种核函数：

Epanechnikov核：

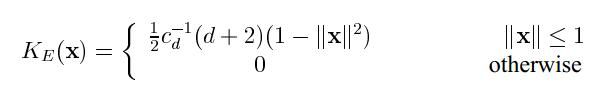
剖面函数位为：

高斯核：

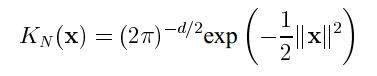
剖面函数为：

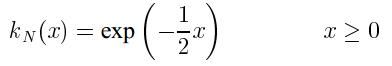
在使用时，对核函数进行对称的截断，可以得到有限的支撑集。本文的核函数都是径向对称的核函数，满足：

在x≥0时，定义核函数的剖面函数为k(x)，c_(k,d)是归一化常量，并假设其为严格正实性。
采用只有一个参数的核密度估计得到如下公式：

采用剖面函数使得上式变为：

核函数这种东西，有可能说的不够明白，想深入了解的可以再找找其他相关资料。

Meanshift算法的推导过程：

给定d维空间R^d的n个样本点 ,i=1,…,n,在空间中任选一点x，那么Mean Shift向量的基本形式定义为:

S_k是一个半径为h的高维球区域,满足以下关系的y点的集合

k表示在这n个样本点xi中,有k个点落入Sk区域中。

简单地说，在d维空间中，任选一个点，然后以这个点为圆心，h为半径做一个高维球（因为有d维，d可能大于2，所以是高维球）。落在这个球内的所有点和圆心都会产生一个向量，向量是以圆心为起点落在球内的点为终点。然后把这些向量都相加。相加的结果就是Meanshift向量。

如下图所示。其中黄色箭头就是M_h（meanshift向量）

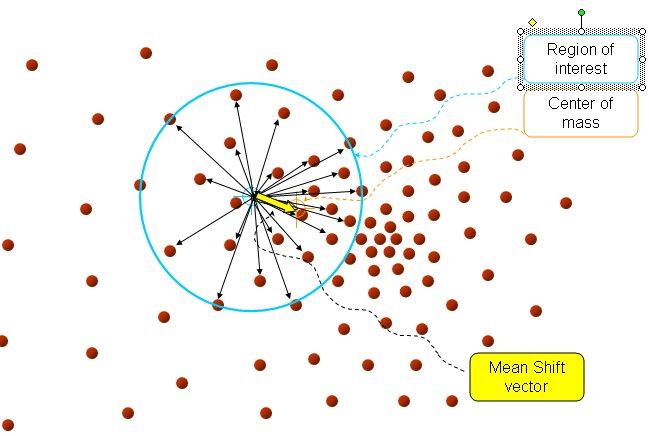
再以meanshift向量的终点为圆心，做一个高维的球。如下图所以，重复以上步骤，就可得到一个meanshift向量。如此重复下去，meanshift算法可以收敛到概率密度最大的地方（也就是最稠密的地方）。

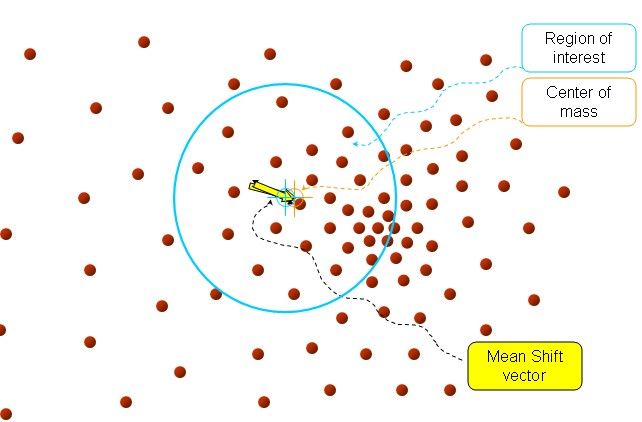
最终的结果如下：

Meanshift算法中加入核函数，那么，meanshift算法变形为:

其中k(x)为核函数，h为半径， c_(k,d)/nh^d 为单位密度，要使得上式f得到最大，对其求导，得到：

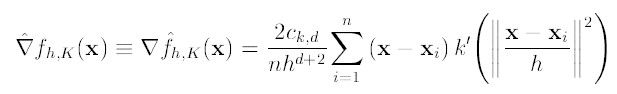
令g(x) = -k’(x)，K(x)叫做G(x)的影子核，那么上式可以表示为：

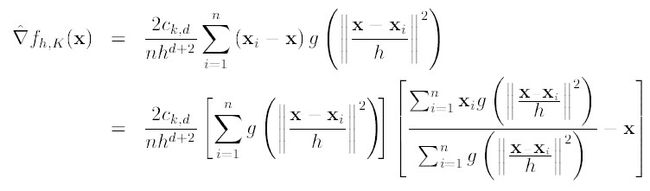
对于上式，如果采用高斯核，那么，可分为三部分，第一项部分为：

第二部分相当于一个meanshift向量的式子：

第三部分是一个系数：2/h² ，那么该式可以表示为：

下面分析上式的构成，其构成比较清晰，如下所示：

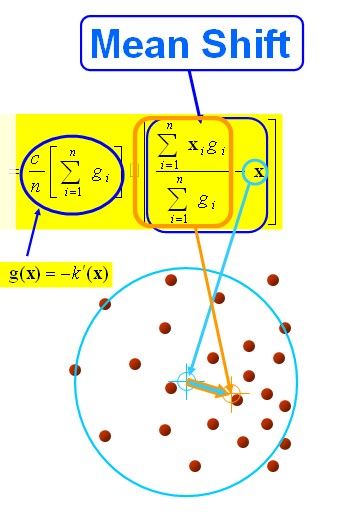
要使整个式子为0，当且仅当m_h,G(x) = 0，可以得出新的圆心坐标：

下面介绍Meanshift算法的计算过程

1、选择空间中点x为圆心，以h为半径，做一个高维球，落在球内的点记为x_i

2、计算m_h,G(x)

3、如果m_h,G(x)<ε，退出程序；如果m_h,G(x)>ε，则利用下式

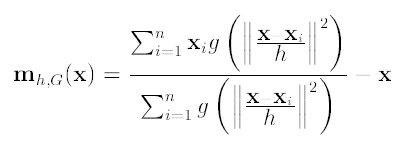
计算出新的圆心坐标（下图），并跳转至步骤1

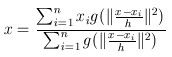
由于在计算的时候加入了与密度相关的权值，使得步长不仅与梯度大小有关，也与该点的密度大小有关，密度大的地方步长小，更精确，密度小的地方，步长大，收敛速度快，在满足条件时，就会收敛到附近的峰值。