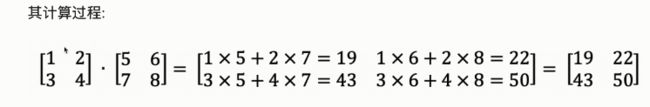Python数据分析 - 机器学习笔记:第一章数据分析 - 1.2.4.矩阵和矢量运算
前言:本文是学习网易微专业的《python全栈工程师》 中的《数据分析 - 机器学习工程师》专题的课程笔记,欢迎学习交流。
一、课程目标
- 掌握矩阵的创建方法
- 掌握矢量运算的基本方法
二、详情解读
2.1.掌握矩阵的创建方法
2.1.1.区分
- 矩阵:矩阵是
numpy库的一种对象 - 矩阵 ≠ \neq = 二维数组
1.创建矩阵:
方法一:
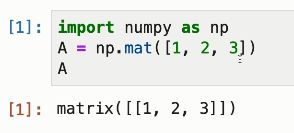
import numpy as np
A = np.mat([1, 2, 3])
A.shape
B = np.mat('1 2 3; 4 5 6; 7 8 9') # 方阵
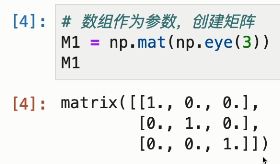
# 数组作为参数,创建矩阵
M1 = np.mat(np.eye(3))
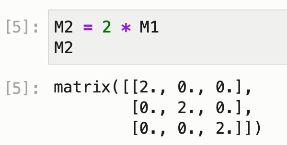
M2 = 2 * M1
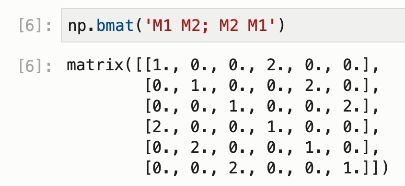
np.bmat('M1 M2; M2 M1')
先初始化两个数组:
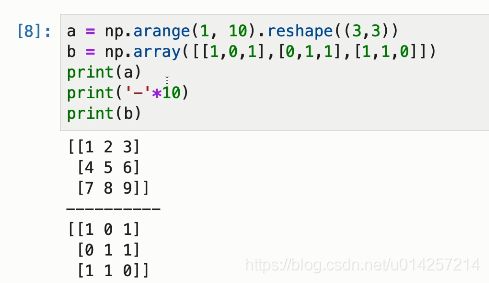
a = np.arange(1, 10).reshape((3, 3))
b = np.array([[1, 0, 1], [0, 1, 1], [1, 1, 0]])
print(a)
print('-'*10)
print(b)
a * b
A = np.mat(a)
B = np.mat(b)
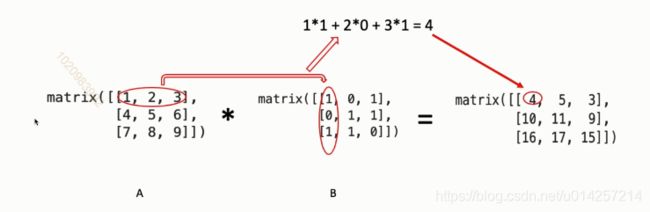
A * B
np.dot(a, b)
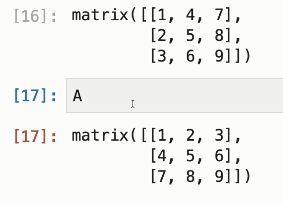
A.T
2.2.矢量运算
2.2.1.标量积
- 标量积(英语:
Scalar Product)是两个矢量相乘的一种方式和结果。 - 也被称为数量积、点积(英语:
Dot Product)、内积(英语:Inner Product)。 - 按照这种方式两个矢量相乘的结果是一个标量。
代数理解:
假设两个矢量 a ⃗ = [ a 1 , a 2 , a 3 , . . . a n ] \vec{a} = [a_1, a_2, a_3, ... a_n] a=[a1,a2,a3,...an] 和 b ⃗ = [ b 1 , b 2 , b 3 , . . . . b n ] \vec{b} = [b_1, b_2, b_3, .... b_n] b=[b1,b2,b3,....bn],它们的点积定义为:
a ⃗ ⋅ b ⃗ = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + . . . + a n b n \vec{a} \cdot \vec{b} = \sum_{i=1}^na_ib_i = a_1b_1 + a_2b_2 + ... + a_nb_n a⋅b=i=1∑naibi=a1b1+a2b2+...+anbn
或者 a ⃗ ⋅ b ⃗ = ∣ a ⃗ b ⃗ T ∣ \vec{a}\cdot\vec{b} = |\vec{a}\vec{b}^T| a⋅b=∣abT∣
其中 b ⃗ T \vec{b}^T bT是向量 b ⃗ \vec{b} b的转置,而 ∣ a ⃗ b ⃗ T ∣ |\vec{a}\vec{b}^T| ∣abT∣是 a ⃗ b ⃗ T \vec{a}\vec{b}^T abT的行列式。
几何理解:
以平面坐标系中的两个矢量为例,两个矢量 a ⃗ \vec{a} a和 b ⃗ \vec{b} b,它们的夹角是 θ \theta θ,则
a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ c o s θ \vec{a}\cdot\vec{b} = |\vec{a}||\vec{b}|cos\theta a⋅b=∣a∣∣b∣cosθ
示例:
计算函数:np.dot()
c = np.array([[1, 2], [3, 4]])
d = np.array([[5, 6], [7, 8]])
np.dot(c, d)
np.inner(c, d)
运行结果:

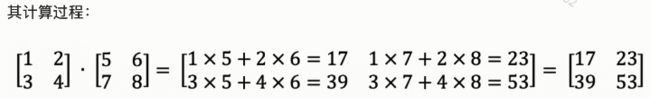
对于二维数组,1轴是最后轴(last axes),np.inner()即是将两个数组1轴上的元素分别对应相乘并求和,并得到最终的数组。
2.2.2.矢量积
- 矢量积(英语:
Vector Product),又可以称为叉积(英语:Cross Product)或外积(英语:Outer Product) - 其运算结果是一个矢量,并且矢量方向与原来两个矢量所构成的平面垂直
代数理解:
我们以三维坐标系中的两个矢量为例,即 a ⃗ = a x i ⃗ + a y j ⃗ + a z k ⃗ \vec{a} = a_x\vec{i} + a_y\vec{j} + a_z\vec{k} a=axi+ayj+azk和 b ⃗ = b x i ⃗ + b y j ⃗ + b z k ⃗ \vec{b} = b_x\vec{i} + b_y\vec{j} + b_z\vec{k} b=bxi+byj+bzk,则:
a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ a x a y a z b x b y b z ∣ = ( a y b z − a z b y ) i ⃗ + ( a z b x − a x b z ) j ⃗ + ( a x b y − a y b x ) k ⃗ \vec{a}\times\vec{b} =\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ a_x & a_y & a_z\\ b_x & b_y & b_z\\ \end{vmatrix} = (a_yb_z - a_zb_y)\vec{i} + (a_zb_x - a_xb_z)\vec{j} + (a_xb_y - a_yb_x)\vec{k} a×b=∣∣∣∣∣∣iaxbxjaybykazbz∣∣∣∣∣∣=(aybz−azby)i+(azbx−axbz)j+(axby−aybx)k
代数理解:
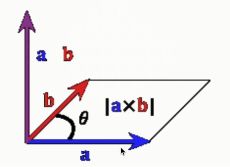
还是以平面坐标系中的两个矢量为例,两个矢量 a ⃗ \vec{a} a和 b ⃗ \vec{b} b,它们的夹角是 θ \theta θ,如果对这两个矢量计算矢量积,最后结果的大小等于这两个矢量为相邻两边的平等四边形的面积,即:
a ⃗ × b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ s i n θ \vec{a}\times\vec{b} = |\vec{a}||\vec{b}|sin\theta a×b=∣a∣∣b∣sinθ
numpy中计算矢量积:np.cross()
v = np.array([1, 2, 3])
b = np.array([9, 8, 7])
np.cross(v, b)
运行结果:
![]()
计算过程:
∣ i j k 1 2 3 9 8 7 ∣ = ( 2 × 7 − 3 × 8 ) i ⃗ + ( 1 × 8 − 2 × 9 ) j ⃗ = − 10 i ⃗ + 20 j ⃗ − 10 k ⃗ \begin{vmatrix} i & j & k \\ 1 & 2 & 3 \\ 9 & 8 & 7\\ \end{vmatrix} = (2 \times 7 - 3 \times 8)\vec{i} + (1\times8 - 2\times 9)\vec{j} = -10\vec{i} + 20\vec{j} - 10\vec{k} ∣∣∣∣∣∣i19j28k37∣∣∣∣∣∣=(2×7−3×8)i+(1×8−2×9)j=−10i+20j−10k
np.cross()的参数不仅仅可以是一维数组(矢量),还可以是多维。
三、课程小结
- 01 矩阵乘法
- 02 标量积、矢量积