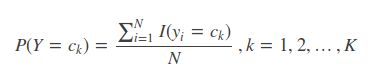让你奶奶轻松搞懂Naive Bayes的理论与实践

stay simple,stay naive

hahaha，今天连文章的第一句话都改了。
不过，我标题党了... ...毕竟你奶奶可能连概率是什么都不知道，而我这里没有基础的教学。之所以取这个名字是因为，你只要顺着我的思路认真读下去，可以清楚地融会贯通Naive Bayes，搞懂它的原理。

朴素贝叶斯（Naive Bayes）是基于贝叶斯定理和特征条件独立假设的分类方法。
换句话说，Naive Bayes的构造基础是贝叶斯定理，基本数学假设是：输入数据在各个维度上的特征被分类的条件概率之间是相互独立的。

本文将从朴素贝叶斯的算法出发，一点一点的剖析算法的原理，分析清楚朴素贝叶斯为什么要这样进行运算。
最后。上手实践。

朴素贝叶斯算法(naive Bayes algorithm)
输入：训练数据 T = {(x₁,y₁),(x₂,y₂),(x₃,y₃),···,(x_N,y_N)}
其中x_i = (x_i⁽¹⁾, x_i⁽²⁾, ..., x_i⁽ⁿ⁾)^T，x_i代表一条实例，这个数据集中每一条实例都由n个维度组成。
x_i^(j)是训练数据中第i个样本的第j维特征。
x_i^(j)∈{a_j1, a_j2, a_j3, a_j4, ..., a_jS}，说明j维可以在a这个集合中取值。
y_i是x_i这个实例对应的类别，有可能是c₁，c₂，c₃，··· ， c_K。
输出：实例x的分类

计算先验概率及条件概率
根据输入的数据x_i = (x_i⁽¹⁾, x_i⁽²⁾, ..., x_i⁽ⁿ⁾)^T计算后验概率。
最大化后验概率，得到x_i对应的类别。

我知道你没看懂。
因为上述算法只是一个引子，请认真阅读下边的内容，我会从头开始分析，讲清楚上边的算法为什么是这样，引导你真正懂得朴素贝叶斯。

注：
= = 经过之前有一篇文章受累不讨好地使用Latex手打公式，最后还出现了下图错误无法加载的情况，这次我决定手写，同学们就凑合看吧。O__O "…

教训

用通俗的话来讲，朴素贝叶斯，就是要学习一个X与Y的联合概率分布，这个联合概率分布就代表了X与某个Y之间的组合的可能性。这个联合概率分布学好了，就意味着朴素贝叶斯这个模型学好了。有了这个联合概率分布，再给一个输入值x，我想，学过概率的人都应该知道怎么计算在x的条件下的条件概率吧。这就是朴素贝叶斯的基本思路，非常简单，具体怎么计算，向下看。

在使用朴素贝叶斯分类时，有给定的输入x, 和训练得到的P(X, Y)，就可以计算得到模型的后验概率分布P(Y = c_k | X = x)，也就是说得到了在X = x的条件下Y = c_k的概率。最大化P(Y = c_k | X = x)，等同于Y = c_k的概率最大时的那个c_k，就是这个模型的输出，就是输入x的类别。最大化后验概率，这是后话。这里就来解释一下这个后验概率。

公式推导

请看上图，公式（1）代表了条件独立性假设，说明X = x⁽ⁿ⁾相互之间是彼此独立的。
公式（2）就是我们所需要的后验概率，是我们要求的在输入x的条件下各种类别的概率，我们需要做的就是计算这个公式。为了让公式（1）可以在公式（2）中发挥作用，我们需要将公式（2）变形，变出含有公式（1）的样子，具体步骤见上图。
然后将公式（1）带入公式（2）。见公式（3），就是我们的目标函数，也就是本节题目所说的后验概率。

好了，后验概率已经出来了。
然后的问题是，我们为什么认为最大化后验概率就可以得到我们想要的结果呢。
来看下图告诉你为什么。
下图中最上边的公式大家应该认识，是0-1损失函数。在预测值和真实值相等的时候，函数为0；预测值和真实值不等的时候，函数为1。
看公式（5），是期望风险函数。接下来将这个风险期望变形。具体情况见下图，由公式（5）到公式（6）的转化。优化一个模型，我们需要最小化他的期望风险函数，也就是最小化公式（6）。具体情况见下图，推导地也很清楚。最后可以发现最小化使用0-1损失函数的风险函数就是最大化后验概率。

知道了为什么要最大化后验概率，后验概率也有了，进入到算法的最后一步，最大化这个后验概率。

看上图，看公式（4）。注意注意注意：在此纠正一下上图中的错误：公式（4）右边的那行字有误，并不是最大化c_k，而是最大化这个后验概率从而得到使这个后验概率最大的c_k。
把公式（3）带入公式（4），观察公式（4）第2行中的分母，他用一个求和符号把每一个c求和，可知P(c₁),P(c₂),...,P(c_k)的和为1。因此分母中的内容其实与c_k无关。因为公式（4）被最大化是用来寻找c_k的值，所以与c_k无关的部分为了简化计算舍去。于是得到最终最大化后验概率的公式。

公式推导

到此为止！公式推导部分结束。你已经跟着我的思路得出了一个朴素贝叶斯的输出的最终公式。

y = argmax_c_kP(Y = c_k) ∏_jP(X^(j) = x^(j) | Y = c_k)

对的，前边说了什么基本理论，什么公式推导，你可以暂时忘掉，因为到了这一步，我们的任务仅仅是计算上边这个公式的值，这个公式的值就是朴素贝叶斯的输出值。

我们要计算什么，相信你此时已经非常了解了。然后，算。
这就来到了文章开头的算法的第一个步骤：

计算先验概率及条件概率

y = argmax_c_kP(Y = c_k) ∏_jP(X^(j) = x^(j) | Y = c_k) 这个公式就是由Y的先验概率和条件概率相乘得到的，所以为了计算这个公式，我们要在这里计算先验概率及条件概率。
这里提供两种方式来估计这两种概率：

极大似然估计
贝叶斯估计

1. 极大似然估计

先验概率P(Y = c~k~) 的极大似然估计

条件概率P(X^(j)^ = x^(j)^ | Y = c~k~) 的极大似然估计

2. 贝叶斯估计

然而用极大似然估计可能会出现所要估计的概率值为0的情况，0就会影响后验概率的计算结果，使分类产生偏差。因此我们在极大似然估计的分子和分母部分分别加上一个小尾巴，防止0的出现。改进之后的估计方法叫做贝叶斯估计。

先验概率P(Y = c~k~) 的贝叶斯估计

条件概率P(X^^(j)^ = x^(j)^ | Y = c~k~) 的贝叶斯估计

根据输入的数据x_i = (x_i⁽¹⁾, x_i⁽²⁾, ..., x_i⁽ⁿ⁾)^T计算P(Y = c_k) ∏_jP(X^(j) = x^(j) | Y = c_k)

上一步骤中已经有了条件概率的计算公式，在这一步骤中根据输入的x通过公式计算出我们需要的条件概率。

最大化后验概率，得到x_i对应的类别

到了这一步，整个朴素贝叶斯的计算就完成了。
理论结合实践，下边一道例题让你对上边所讲的理论部分有更深入的理解。

例题

根据下表中的训练数据来训练一个贝叶斯分类器，来确定输入值x = (2, S)的类别。
下表中X¹，X²为输入值的2个维度，Y为输出值，可以看出是一个分类问题，分为1和-1两类。

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X¹	1	1	1	1	1	2	2	2	2	2	3	3	3	3	3
X²	S	M	M	S	S	S	M	M	L	L	L	M	M	L	L
Y	-1	-1	1	1	-1	-1	-1	1	1	1	1	1	1	1	-1

解

上图的解题过程清晰易懂，模拟了前文讲解的朴素贝叶斯的过程.

到了代码实现的时间。
这次使用的是20类新闻文本作为数据集。

# coding=utf-8
# import 与这个数据集相关的包
from sklearn.datasets import fetch_20newsgroups
# 与鸢尾不同的是，这个数据集无法直接加载，而是需要从网络下载数据，不过基本套路与上一篇的knn差不多
news = fetch_20newsgroups(subset='all')

print len(news.data)
print news.data[0]

展示数据集样例：可以看出有18846条数据，下边的内容为其中的第1条。

18846
From: Mamatha Devineni Ratnam 
Subject: Pens fans reactions
Organization: Post Office, Carnegie Mellon, Pittsburgh, PA
Lines: 12
NNTP-Posting-Host: po4.andrew.cmu.edu

I am sure some bashers of Pens fans are pretty confused about the lack
of any kind of posts about the recent Pens massacre of the Devils. Actually,
I am  bit puzzled too and a bit relieved. However, I am going to put an end
to non-PIttsburghers' relief with a bit of praise for the Pens. Man, they
are killing those Devils worse than I thought. Jagr just showed you why
he is much better than his regular season stats. He is also a lot
fo fun to watch in the playoffs. Bowman should let JAgr have a lot of
fun in the next couple of games since the Pens are going to beat the pulp out of Jersey anyway. I was very disappointed not to see the Islanders lose the final
regular season game.          PENS RULE!!!

然后，还是熟悉的操作，分割测试集和训练集。分割结果就不向上贴了。

from sklearn.cross_validation import train_test_split

X_train, X_test, Y_train, Y_test = train_test_split(news.data, news.target, test_size=0.25, random_state=33)

然后，就是要导入模型开始训练了。
等等，是不是发现了有一些什么不一样？上次的鸢尾数据是什么样的？这次呢？机器认识这次的自然语言吗？
所以在这里需要有一个步骤是将数据中的文本转化为特征向量。

# 文本与特征向量转化的模块
from sklearn.feature_extraction.text import CountVectorizer
# 这里的操作就像上一次的数据标准化
w2v = CountVectorizer()
X_train = w2v.fit_transform(X_train)
X_test = w2v.transform(X_test)

现在就可以导入模型了。

from sklearn.naive_bayes import MultinomialNB

NB = MultinomialNB()
# 训练
NB.fit(X_train, Y_train)
# 测试
predict = NB.predict(X_test)

print NB.score(X_test, Y_test)

0.839770797963

ok,大功告成。
炎炎夏日去喝杯冰饮吧。

参考文献：
统计学方法 | python机器学习及实践

如果你也喜欢机器学习，并且也像我一样在ML之路上努力，请关注我，我会进行不定期更新，总有一些可以帮到你。

文中公式推导为我个人理解，不保证理解完全正确，望指正
部分图片来自网络，部分本人手写
最后，字丑勿怪，但是人帅呀