腾讯移动端三面总结
昨天终于迎来了腾讯的第三轮的技术面,总共三个半小时的轮流轰炸,出来的时候自己已是头晕脑涨,腾讯的面试官也很牛逼,问了很多根本答不上来的问题。
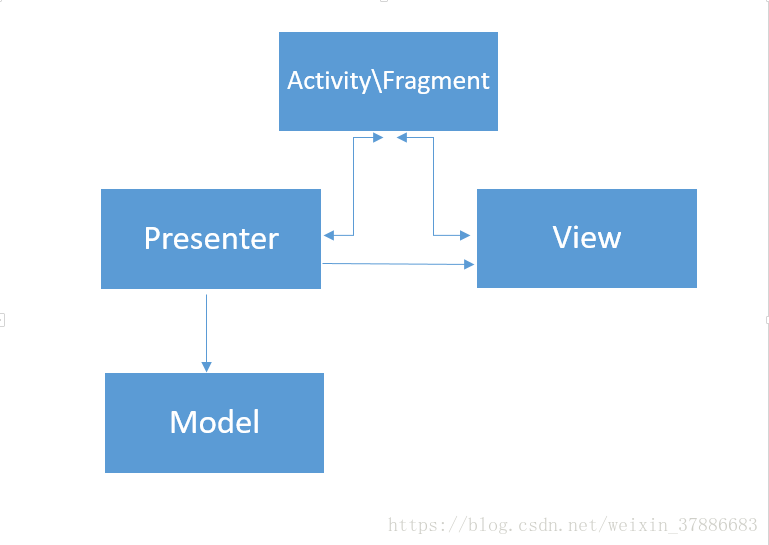
1. 请你画出MVP架构图,并解释一遍它的运作流程。比如网络操作
我的理解是这样的,Activity/Fragment只有IPresenter和IView的接口,它只负责绑定,也就是注入IPresenter对IModel的依赖,IPresenter对IView的依赖。View层负责UI层的显示,因此,不需要在Activity或者Fragment处理UI,它们的代码将变得十分简洁。页面的初始化调用presenter.init()即可。
2. 解释一下页面展示数据获取的数据来源。
我的回答是[Cache][DataBase]Service
fun getListData: Data(){
var data: Data? = null
data = getDataFromCache()
data?.let{return it}
data = getDataFromDataBase()
data?.let{return it}
data = getDataFromService()
data?.let{return it}
}3. 多线程会导致什么问题,应该怎么解决?
这个问题我认为主要是问多线程的缺点,所以我就答了几点缺点。
- 线程也是程序,所以线程需要占用内存,线程越多占用内存也越多
- 多线程需要协调和管理,所以需要CPU时间跟踪线程
- 线程之间对共享资源的访问会相互影响,必须解决竞用共享资源的问题
- 线程太多会导致控制太复杂,最终可能造成很多Bug
4. Android进程的优先级是怎样的?
Android有一个淘汰机制,会根据App的运行状态设置一个进程的优先级(oom_adj),然后根据内存的紧张程度,把那些优先级低(oom_adj值大)的进程kill掉,以保证其他的进程能够有足够的内存使用
粗略的划分如下,优先级从高到低:
- 前台进程。前台进程是目前正在屏幕上显示的进程和一些系统进程,也就是和用户正在交互的进程。
- 可见进程。可见进程指部分程序界面能够被用户看见,却不在前台与用户交互的进程。如弹出Dialog的Activity
- 服务进程。服务进程是通过 startService() 方法启动的进程,但不属于前台进程和可见进程
- 后台进程。后台进程指的是目前对用户不可见的进程。
- 空进程。空进程指的是在这些进程内部,没有任何东西在运行。
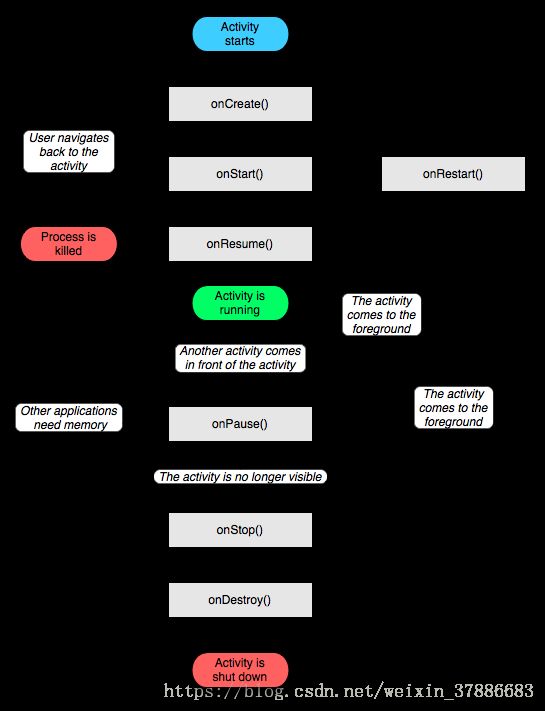
5. 说一下Activity的生命周期
6. onStar和onResume方法的区别是什么?什么时候用onStart,什么时候用onResume.
从上图可以知道,onResume方法的调用次数应该会比onStar方法高。因此也可以从性能的角度出发考虑。
- onStart()是activity界面被显示出来的时候执行的,用户可见,包括有一个activity在他上面,但没有将它完全覆盖,用户可以看到部分activity但不能与它交互
- onResume()是当该activity与用户能进行交互时被执行,用户可以获得activity的焦点,能够与用户交互。
7. 说一下冒泡排序和选择排序的区别?
- 冒泡算法,每次比较如果发现较小(或较大)的元素在后面,就交换两个相邻的元素。
- 选择排序:先不调换位置,先从A[1]开始逐个检查,看哪个数最小就记下该数所在的位置P,等一躺扫描完毕,再把A[P]和A[1]对调,这时A[1]到A[N]中最小的数据就换到了最前面的位置。
选择排序每扫描一遍数组,只需要一次真正的交换,而冒泡可能需要很多次。比较的次数是一样的
8. 冒泡排序最优的时间复杂度?
O(n)。使用一个标记位标记是否发生了交换。
public void bubbleSort(int arr[]) {
boolean didSwap;
for(int i = 0, len = arr.length; i < len - 1; i++) {
didSwap = false;
for(int j = 0; j < len - i - 1; j++) {
if(arr[j + 1] < arr[j]) {
swap(arr, j, j + 1);
didSwap = true;
}
}
if(didSwap == false)
return;
}
9. 一棵没有特定顺序的二叉树,如何存放在文件中?
一开始,我想到了二叉树补全法。如果这个节点为空,则使用特殊字符将这课二叉树补全,变成一颗完全二叉树,再使用数组进行存储,写入文件中。但是面试官提示我这个方法不合理,因为使用了补全操作,对于一颗很不规则的二叉树,将会占用非常大的存储空间,并且修改了二叉树的属性。后面觉得其实不用将二叉树补全,我们只需要在空节点那么标记一次,就能证明这个结点一下已经没有节点了。因此,我们不需要多次重复标记。
面试完后,在网上也看到了一个比较好的方法。大概的思路是:给每个节点按照它在二叉树中的位置给与其一个唯一的编号,那么只要记录每个节点的编号和相关信息,就能够记录一整棵二叉树。
编号方式:用n(x)表示节点x的编号(如下图)
1、如果x是根节点,那么n(x)=1
2、如果x不是根节点,那么x有亲节点p;如果x是p的左子节点,那么n(x)=n(p)*2,否则n(x)=n(p)*2+1
在文件中记录格式:
节点总数
节点1编号 节点1信息
节点2编号 节点2信息.......
10. 手写代码,给一个int的数组,将其移动k位。如array = [1,2,3,4,5], k = 2, 则移动后的array为[4,5,1,2,3].
因为当时只给了15分钟左右的时间,所以我只写到了两种比较简单的解法。也即解法1和解法2.
解法1:记录最后一位,然后将前面n-1位向后移动一位。(注意越界问题)
public void moveArray(int[] array, int k) {
if(k <= 0){
return;
}
int length = array.length;
// 假设移动的位数是k,那么无论是向右还是向左移动k+n*length个位置之后,移动到还是原来的位置
int step = k % length;
int temp = 0;
for(int i = 0; i < step; i++) {
// 这个temp保存的是这个数组的一个元素
temp = array[length - 1];
for(int j = length - 2; j >= 0; j--) {
// 让后一个元素等于前面的元素,相当于后面的元素是被前面的元素覆盖了
array[j+1] = array[j];
}
// 第一个元素在每一个循环结束之后就要把之前的临时变量填充后进去
// 因为临时变量保存的是每一次的最后一个位置的元素
array[0] = temp;
}
}解法2:开辟一个新的数组,截取旧数组。
public int[] moveArray(int[] array, int k) {
if(k <= 0){
return;
}
int length = array.length;
int step = k % length;
int[] newArray = new int[length];
// 重复length次把元素从旧位置移动和到新位置
for(int i = 0; i < length; i++) {
// 求出元素新的位置
// 注意是要取模的
/**
* 加上i=6(就是最后一个元素)
* 移动的位置是3
* 那么 (6+3)%7 = 2
* 索引原来数组的索引为6(最后一个元素)
* 在新数组中的索引为2.
*/
int newPosition = (i + step) % length;
newArray[newPosition] = array[i];
}
return newArray;
}11. 设计QQ传文件功能,并画出模块设计图。
12. 说一下防火墙穿越的实现原理
13. 加密算法和加密原理
14. Https实现原理
15. 手写代码,无限大整数转16进制
17. 讲解一下登陆时密码加密过程
18. 推理题
宴会上,人们都带着白色或者黑色帽子,其中至少有一个人带黑色帽子,每个人都能看到别人帽子的颜色,看不到自己帽子的颜色。假设每个人都足够聪明,如果在熄灯的时候你觉得你自己带了黑色帽子,就鼓掌。
第一次熄灯,没人鼓掌。。。。。。
第二次熄灯,没人鼓掌。。。。。。
第三次熄灯,有人鼓掌。。。。。。
请问有多少个人带了黑色帽子?
本来写了20多个问题,发表的时候网络出问题,没保存草稿。草稿箱只剩下10个问题了。晕死~~~~只贴上记得的问题,不打算继续补充了