NLP(08)_RNN神经网络语言模型

从传统语言模型到神经网络语言模型

我们将学习到如何使用KenLM工具构建语言模型，并使用它完成一个典型的“智能纠错”文本任务。

参考资料:

• Andrej Karpathy的RNN博客
• Language Model: A Survey of the State-of-the-Art Technology

我们从基于n-gram的传统统计语言模型，过渡到典型的前馈神经网络模型和循环神经网络模型。

传统语言模型

从前面的内容，大家可以看到传统的语言模型构建方法是基于统计，比如bigram或者n-gram语言模型，是对n个连续的单词出现概率进行建模。这类模型基于马尔可夫假设，将n个单词出现的概率：$p(w_1,w_2,\dots ,w_n)$ 的估计任务分解为依次估计每个单词出现的条件概率。出于计算和推导便利性的考虑，这个条件不是基于该单词出现之前所有出现的单词，而是前m个单词：

$$p(w_n|w_{n-1},w_{n-2},\cdots ,w_1)\approx p(w_n|w_{n-1},\cdots ,w_{n-m})$$

上述公式表明，传统的语言模型假设我们对于一个单词在某个位置出现概率的估计可以通过计算该单词与前面m个单词同时出现频率相对于前面的m个单词同时出现的频率的比获得。这是朴素贝叶斯的思路。

1. 如果m为0，我们的估计只基于该单词在全部文本中相对于其他所有单词的频率，这个模型就是unigram模型；
2. 如果m为1，那么这个模型就是常见的bigram模型，
3. 如果m为2，那么这个模型就是trigram模型，其计算公式如下：

$$p(w_n|w_{n-1},w_{n-2})=\frac{\text{count}(w_n,w_{n-1},w_{n-2})}{{\sum }_j\text{count}(w_j,w_{n-1},w_{n-2})}$$

传统n-gram模型简单实用，但是数据的稀疏性和泛化能力有很大的问题。

文本稀疏性

因为n-gram模型只能对文本中出现的单词或者单词组进行建模，当新的文本中出现意义相近但是没有在训练文本中出现的单词或者单词组的时候，传统离散模型无法正确计算这些训练样本中未出现的单词的应有概率，他们都会被赋予0概率预测值。这是非常不符合语言规律的事情。

举个例来讲，在一组旅游新闻中，“酒店”和“宾馆”是同义词，可以交替出现，但是假设整个训练集中没有出现过“宾馆”这个单词，那么在传统模型中对于“宾馆”这个词的出现概率会输出接近于0的结果。

但是上述相似例子在实际生活中却是非常比比皆是，由于计算资源与数据的限制，我们经常会发现模型在使用中遇见在整个训练集中从未出现的单词组的情况。为了解决这种矛盾，传统方法是引入一些平滑或者back-off的技巧，整体上，效果并没有预想的好。

泛化能力不佳

除了对未出现的单词本身进行预测非常困难之外，离散模型还依赖于固定单词组合，需要完全的模式匹配，否则也无法正确输出单词组出现的概率。假设新闻中一段话是“食物可口的酒店”，这句话和“餐食美味的宾馆”本身意思相近，一个好的语言模型是应该能够识别出后面这句话与前面那句无论从语法还是语义上都是非常近似，应该有近似的概率分布，但是离散模型是无法达到这个要求的。这就使得此类模型的泛化能力不足。Bengio等人在发布其神经网络语言模型的时候就专门指出了传统离散模型的这个弱点。

此外，对于n-gram模型来说，第一个公式的马尔可夫假设太强。人在对文字进行处理的时候，是能够将很长一段上下文纳入考虑，但是n-gram的离散模型只考虑待预测单词前面的n-1个单词，这个马尔可夫假设与实际情况并不相符，使得第一个公式中两个概率近似的要求其实并不能满足。

离散模型在计算上还存在“维度诅咒”的困难。从上面的公式可以看出，当我们将更多单词组合挑出来之后才能更精准地预测特定单词组出现的概率，但是这种组合的量是非常大的。假设我们的词库有一万个独立单词，对于一个包含4个单词的词组模式，潜在的单词组合多达$10000^4$。这使得突破一定的预测精度非常困难。

神经网络语言模型

传统语言模型的上述几个内在缺陷使得人们开始把目光转向神经网络模型，期望深度学习技术能够自动化地学习代表语法和语义的特征，解决稀疏性问题，并提高泛化能力。我们这里主要介绍两类神经网络模型：前馈神经网络模型（FFLM）和循环神经网络模型（RNNLM）。前者主要设计来解决稀疏性问题，而后者主要设计来解决泛化能力，尤其是对长上下文信息的处理。在实际工作中，基于循环神经网络及其变种的模型已经实现了非常好的效果。

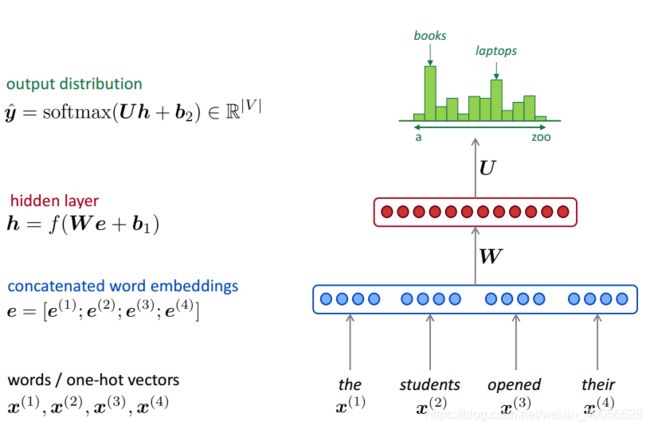
我们前面提到，语言模型的一个主要任务就是要解决给定到当前的上下文的文字信息，如何估计现在每一个单词出现的概率。Bengio等人提出的第一个前馈神经网络模型利用一个三层，包含一个嵌入层、一个全连接层、一个输出层，的全连接神经网络模型来估计给定n-1个上文的情况下，第n个单词出现的概率。其架构如下图所示：

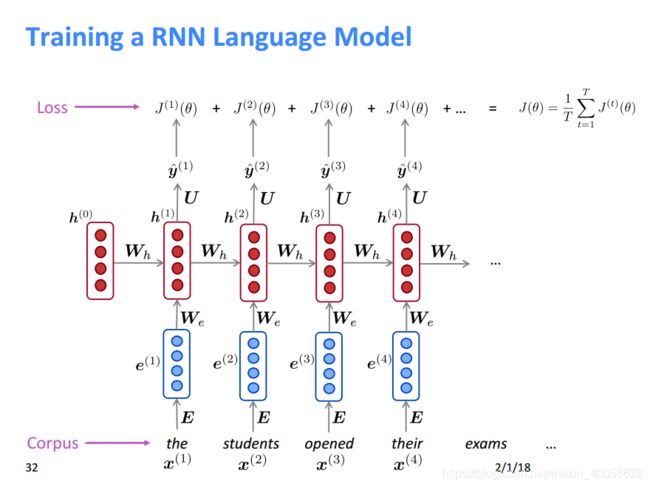
RNN语言模型训练过程

另一类循环神经网络模型不要求固定窗口的数据训练。FFLM假设每个输入都是独立的，但是这个假设并不合理。经常一起出现的单词以后也经常出现的概率会更高，并且当前应该出现的词通常是由前面一段文字决定的，利用这个相关性能提高模型的预测能力。循环神经网络的结构能利用文字的这种上下文序列关系，从而有利于对文字建模。这一点相比FFLM模型更接近人脑对文字的处理模型。比如一个人说："我是中国人，我的母语是___ "。 对于在“__”中需要填写的内容，通过前文的“母语”知道需要是一种语言，通过“中国”知道这个语言需要是“中文”。通过RNNLM能回溯到前两个分句的内容，形成对“母语”，“中国”等上下文的记忆。一个典型的RNNLM模型结构如下图所示。

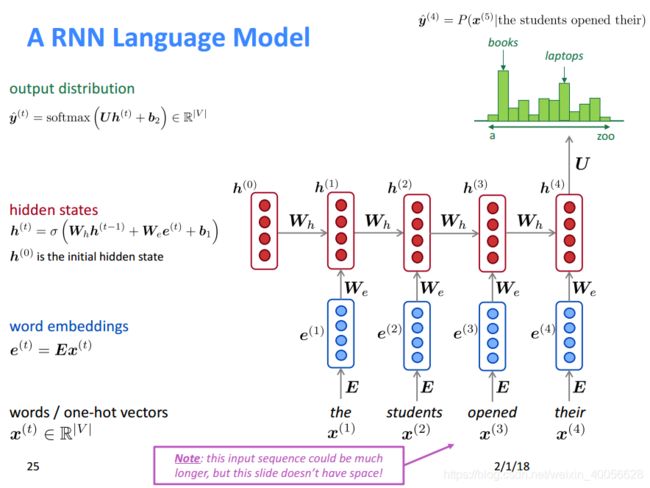
RNN语言模型训练过程

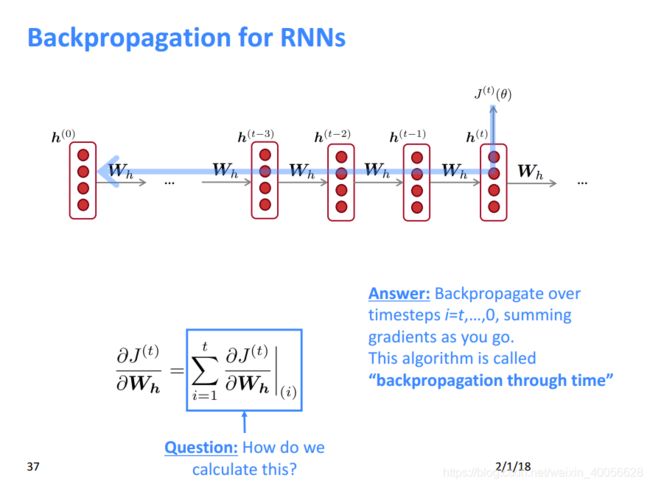
RNN语言模型反向传播

语言模型评估

迷惑度/困惑度/混乱度（perplexity），其基本思想是给测试集的句子赋予较高概率值的语言模型较好,当语言模型训练完之后，测试集中的句子都是正常的句子，那么训练好的模型就是在测试集上的概率越高越好。迷惑度越小，句子概率越大，语言模型越好。

RNN语言模型实现

我们用pytorch来实现一下循环神经网络语言模型。

# 实现参考 https://github.com/pytorch/examples/tree/master/word_language_model
import torch
import torch.nn as nn
import numpy as np
from torch.nn.utils import clip_grad_norm_

class Dictionary(object):
    def __init__(self):
        self.word2idx = {}
        self.idx2word = {}
        self.idx = 0
    
    def add_word(self, word):
        if not word in self.word2idx:
            self.word2idx[word] = self.idx
            self.idx2word[self.idx] = word
            self.idx += 1
    
    def __len__(self):
        return len(self.word2idx)


class Corpus(object):
    def __init__(self):
        self.dictionary = Dictionary()

    def get_data(self, path, batch_size=20):
        # 添加词到字典
        with open(path, 'r') as f:
            tokens = 0
            for line in f:
                words = line.split() + ['']
                tokens += len(words)
                for word in words: 
                    self.dictionary.add_word(word)  
        
        # 对文件做Tokenize
        ids = torch.LongTensor(tokens)
        token = 0
        with open(path, 'r') as f:
            for line in f:
                words = line.split() + ['']
                for word in words:
                    ids[token] = self.dictionary.word2idx[word]
                    token += 1
        num_batches = ids.size(0) // batch_size
        ids = ids[:num_batches*batch_size]
        return ids.view(batch_size, -1)

# 有gpu的情况下使用gpu
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
#device = torch.device('cpu')

# 超参数的设定
embed_size = 128    # 词嵌入的维度
hidden_size = 1024  # LSTM的hidden size
num_layers = 1
num_epochs = 5      # 迭代轮次
num_samples = 1000  # 测试语言模型生成句子时的样本数
batch_size = 20     # 一批样本的数量
seq_length = 30     # 序列长度
learning_rate = 0.002 # 学习率

# 加载数据集
corpus = Corpus()
ids = corpus.get_data('data/train.txt', batch_size)
vocab_size = len(corpus.dictionary)
num_batches = ids.size(1) // seq_length

# RNN语言模型
class RNNLM(nn.Module):
    def __init__(self, vocab_size, embed_size, hidden_size, num_layers):
        super(RNNLM, self).__init__()
        self.embed = nn.Embedding(vocab_size, embed_size)
        self.lstm = nn.LSTM(embed_size, hidden_size, num_layers, batch_first=True)
        self.linear = nn.Linear(hidden_size, vocab_size)
        
    def forward(self, x, h):
        # 词嵌入
        # YOUR CODE HERE
        
        # LSTM前向运算
         # YOUR CODE HERE
        
        # 把结果变更为(batch_size*sequence_length, hidden_size)的维度
         # YOUR CODE HERE
        
        # 全连接
         # YOUR CODE HERE
        return  # YOUR CODE HERE

model = RNNLM(vocab_size, embed_size, hidden_size, num_layers).to(device)

# 损失构建与优化
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

# 反向传播过程“截断”(不复制gradient)
def detach(states):
    return [state.detach() for state in states] 

# 训练模型
for epoch in range(num_epochs):
    # 初始化为0
    # YOUR CODE HERE
    
    for i in range(0, ids.size(1) - seq_length, seq_length):
        # 获取mini batch的输入和输出
        # YOUR CODE HERE
        # YOUR CODE HERE
        
        # 前向运算
        # YOUR CODE HERE
        # YOUR CODE HERE
        # YOUR CODE HERE
        
        # 反向传播与优化
        # YOUR CODE HERE
        # YOUR CODE HERE
        # YOUR CODE HERE
        # YOUR CODE HERE

        step = # YOUR CODE HERE
        if step % 100 == 0:
            print ('全量数据迭代轮次 [{}/{}], Step数[{}/{}], 损失Loss: {:.4f}, 困惑度/Perplexity: {:5.2f}'
                   .format(epoch+1, num_epochs, step, num_batches, loss.item(), np.exp(loss.item())))

# 测试语言模型
with torch.no_grad():
    with open('sample.txt', 'w') as f:
        # 初始化为0
        state = (torch.zeros(num_layers, 1, hidden_size).to(device),
                 torch.zeros(num_layers, 1, hidden_size).to(device))

        # 随机选择一个词作为输入
        prob = torch.ones(vocab_size)
        input = torch.multinomial(prob, num_samples=1).unsqueeze(1).to(device)

        for i in range(num_samples):
            # 从输入词开始，基于语言模型前推计算
            output, state = model(input, state)

            # 做预测
            prob = output.exp()
            word_id = torch.multinomial(prob, num_samples=1).item()

            # 填充预估结果（为下一次预估储备输入数据）
            input.fill_(word_id)

            # 写出输出结果
            word = corpus.dictionary.idx2word[word_id]
            word = '\n' if word == '' else word + ' '
            f.write(word)

            if (i+1) % 100 == 0:
                print('生成了 [{}/{}] 个词，存储到 {}'.format(i+1, num_samples, 'sample.txt'))

# 存储模型的保存点(checkpoints)
torch.save(model.state_dict(), 'model.ckpt')