Levenberg-Marquardt算法与透视变换矩阵优化
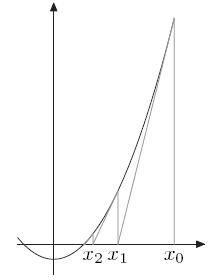
一般来说我们利用牛顿法使用来求f(x)=0的解。求解方法如下：
先对f(x)一阶泰勒展开得
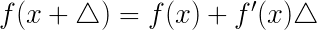
所以我们有
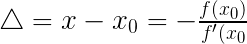，即
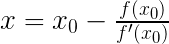
因此也就得到了我们的牛顿迭代公式：
求解最优化问题
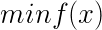
牛顿法首先则是将问题转化为求
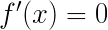
这个方程的根。
一阶展开：
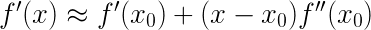
令
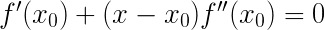
求解得到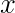
，相比于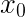
，
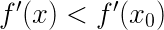
高斯牛顿法
在讲牛顿法的时候，我们举的例子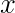是一维的，若如果我们遇到多维的x该如何办呢？这时我们就可以利用雅克比，海赛矩阵之类的来表示高维求导函数了。
比如
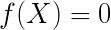,其中![\LARGE X = [x_{0},x_{1},...,x_{n}]](http://img.e-com-net.com/image/info8/02e3ea80ae024579b21cc76be4f05587.gif)
所以我们有雅克比矩阵：
有海赛矩阵：
所以高维牛顿法解最优化问题又可写成：
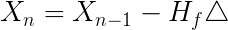
梯度 代替了低维情况中的一阶导
Hessian矩阵代替了二阶导
求逆代替了除法
例：不妨设目标函数为：
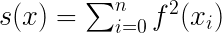
所以梯度向量在方向上的分量：
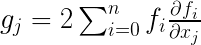
Hessian 矩阵的元素则直接在梯度向量的基础上求导：
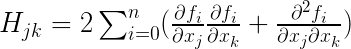
高斯牛顿法的一个小技巧是，将二次偏导省略，于是：
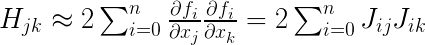
其中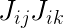
为雅克比矩阵中的第i行j列元素
改写成 矩阵相乘形式：
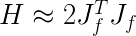
代入牛顿法高维迭代方程的基本形式，得到高斯牛顿法迭代方程：
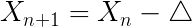,其中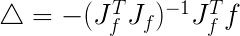
Levenberg-Marquardt算法
引用维基百科的一句话就是：
莱文贝格－马夸特方法（Levenberg–Marquardt algorithm）能提供数非线性最小化（局部最小）的数值解。此算法能借由执行时修改参数达到结合高斯-牛顿算法以及梯度下降法的优点，并对两者之不足作改善（比如高斯-牛顿算法之反矩阵不存在或是初始值离局部极小值太远）
在我看来，就是在高斯牛顿基础上修改了一点。
在高斯牛顿迭代法中，我们已经知道
在莱文贝格－马夸特方法算法中则是
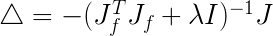
在我看来好像就这点区别。至少我看的维基百科是这样的。
然后Levenberg-Marquardt方法的好处就是在于可以调节:
如果下降太快，使用较小的λ，使之更接近高斯牛顿法
如果下降太慢，使用较大的λ，使之更接近梯度下降法
H矩阵本身已经最优，手动改变了一点测试LM。
close all;
clear all;
clc;
% 返回值 H 是一个3*3的矩阵
% pts1 和 pts2是2*n的坐标矩阵对应特征点的(x,y)坐标
CordReal = load('TestReal.txt');
CordImg = load('TestImg.txt');
pts1 = CordReal(:,1:2)';
pts2 = CordImg(:,1:2)';
n = size(pts1,2);
A = zeros(2*n,9);
A(1:2:2*n,1:2) = pts1';
A(1:2:2*n,3) = 1;
A(2:2:2*n,4:5) = pts1';
A(2:2:2*n,6) = 1;
x1 = pts1(1,:)';
y1 = pts1(2,:)';
x2 = pts2(1,:)';
y2 = pts2(2,:)';
A(1:2:2*n,7) = -x2.*x1;
A(2:2:2*n,7) = -y2.*x1;
A(1:2:2*n,8) = -x2.*y1;
A(2:2:2*n,8) = -y2.*y1;
A(1:2:2*n,9) = -x2;
A(2:2:2*n,9) = -y2;
[evec,D] = eig(A'*A);
H = reshape(evec(:,1),[3,3])';
H = H/H(end); % make H(3,3) = 1
TestReal = load('TestReal.txt');
TestImg = load('TestImg.txt');
N = size(TestReal,1);
TestRealQici = [TestReal(:,1:2),ones(N,1)];
TestImgQici = [TestImg(:,1:2),ones(N,1)];
Result = zeros(N,3);
ImgInvH = zeros(N,3);
for i=1:N
Result(i,1)=((H(1,1)+0.01)*x1(i)+H(1,2)*y1(i)+H(1,3))./(H(3,1)*x1(i)+H(3,2)*y1(i)+H(3,3));
Result(i,2)=(H(2,1)*x1(i)+H(2,2)*y1(i)+H(2,3))./(H(3,1)*x1(i)+H(3,2)*y1(i)+H(3,3));
% Result(i,:)=H*TestRealQici(i,:)';
% ImgInvH(i,:)=H\TestImgQici(i,:)';
end
D = TestImg(:,1:2)-Result(:,1:2);
xlswrite('Result.xls',[TestImgQici Result])
%%
width = round(max(TestReal(:,1)))+50;
height = round(max(TestReal(:,2)))+50;
RealGen = 255*ones(height,width);
imshow(RealGen);
hold on;
plot(TestReal(:,1),TestReal(:,2),'k+');%黑十字
hold on;
plot(ImgInvH(:,1),ImgInvH(:,2),'r.');%红点
%___________
figure();
width = round(max(TestImg(:,1)))+30;
height = round(max(TestImg(:,2)))+30;
ImgGen = 255*ones(height,width);
imshow(ImgGen);
hold on;
plot(TestImg(:,1),TestImg(:,2),'k+');%黑十字
%___________
hold on;
plot(Result(:,1),Result(:,2),'R.');%红点
%%
%H的LM优化
% % 计算函数f的雅克比矩阵，是解析式
% syms h1 h2 h3 h4 h5 h6 h7 h8 h9 xi yi xo yo real;
% % f=(xout-(h1*xin+h2*yin+h3)./(h7*xin+h8*yin+h9)).^2+(yout-(h4*xin+h5*yin+h6)./(h7*xin+h8*yin+h9)).^2; %自己定义误差函数为各点的误差和
% f1=(h1*xi+h2*yi+h3)./(h7*yi+h8*yi+h9);
% f2=(h4*xi+h5*yi+h6)./(h7*yi+h8*yi+h9);
% Jsym = jacobian([f1;f2],[h1 h2 h3 h4 h5 h6 h7 h8 h9])
% 拟合用数据为x1,y1,x2,y2。
% 2. LM算法
% 以近似解H作为迭代初始值
h1_0 = H(1,1);
h2_0 = H(1,2);
h3_0 = H(1,3);
h4_0 = H(2,1);
h5_0 = H(2,2);
h6_0 = H(2,3);
h7_0 = H(3,1);
h8_0 = H(3,2);
h9_0 = H(3,3);
% 数据个数
Ndata=length(x1);
% 参数维数
Nparams=9;
% 迭代最大次数
n_iters=50;
% LM算法的阻尼系数初值
lamda=0.01;
lamda1=0.0001;
% step1: 变量赋值
updateJ=1;
h1_est = h1_0+0.01;
h2_est = h2_0;
h3_est = h3_0;
h4_est = h4_0;
h5_est = h5_0;
h6_est = h6_0;
h7_est = h7_0;
h8_est = h8_0;
h9_est = h9_0;
x_Cord_est = x2;
y_Cord_est = y2;
% step2: 迭代
% step2: 迭代
it = 1; % 迭代计数
id = 1; % 有效结果计数
repeat = 1; % 若误差未减小的情况连续出现次数
while repeat < 10 % 连续出现10次
if updateJ==1
% 根据当前估计值，计算雅克比矩阵
J=zeros(2,Nparams);
Jit = zeros(2*length(x1),Nparams);
DeltaF = zeros(Nparams,2 );
Fh0 =0;
for i=1:length(x1)
Jit(i,:)=[x1(i)./(h7_est*x1(i)+h8_est*y1(i)+h9_est),y1(i)./(h7_est*x1(i)+h8_est*y1(i)+h9_est),1./(h7_est*x1(i)+h8_est*y1(i)+h9_est),0,0,0,(-x1(i)*(h1_est*x1(i)+h2_est*y1(i)+h3_est))./((h7_est*x1(i)+h8_est*y1(i)+h9_est)^2),(-y1(i)*(h1_est*x1(i)+h2_est*y1(i)+h3_est))./((h7_est*x1(i)+h8_est*y1(i)+h9_est)^2),(-(h1_est*x1(i)+h2_est*y1(i)+h3_est))./((h7_est*x1(i)+h8_est*y1(i)+h9_est)^2)];
Jit(i+1,:)=[0,0,0,x1(i)./(h7_est*x1(i)+h8_est*y1(i)+h9_est),y1(i)./(h7_est*x1(i)+h8_est*y1(i)+h9_est),1./(h7_est*x1(i)+h8_est*y1(i)+h9_est),-(x1(i)*(h4_est*x1(i)+h5_est*y1(i)+h6_est))./((h7_est*x1(i)+h8_est*y1(i)+h9_est)^2),(-y1(i)*(h4_est*x1(i)+h5_est*y1(i)+h6_est))./((h7_est*x1(i)+h8_est*y1(i)+h9_est)^2),(-(h4_est*x1(i)+h5_est*y1(i)+h6_est))./((h7_est*x1(i)+h8_est*y1(i)+h9_est)^2)];
end
f1_est = (h1_est*x1+h2_est*y1+h3_est)./(h7_est*x1+h8_est*y1+h9_est);
f2_est = (h4_est*x1+h5_est*y1+h6_est)./(h7_est*x1+h8_est*y1+h9_est);
dx = x_Cord_est- f1_est;
dy = y_Cord_est- f2_est;
d = cat(1,dx,dy);
Hess=Jit'*Jit;
if repeat==1
e=dot(d,d);
end
end
H_lm=Hess+(lamda*eye(Nparams,Nparams));
% 计算步长dp，并根据步长计算新的可能的参数估计值
if(rank(H_lm) == 9)
break;
end
dp=(H_lm)\(Jit'*d(:));
h1_lm=h1_est+dp(1);
h2_lm=h2_est+dp(2);
h3_lm=h3_est+dp(3);
h4_lm=h4_est+dp(4);
h5_lm=h5_est+dp(5);
h6_lm=h6_est+dp(6);
h7_lm=h7_est+dp(7);
h8_lm=h8_est+dp(8);
h9_lm=h9_est+dp(9);
f1_est_lm = (h1_lm*x1+h2_lm*y1+h3_lm)./(h7_lm*x1+h8_lm*y1+h9_lm);
f2_est_lm = (h4_lm*x1+h5_lm*y1+h6_lm)./(h7_lm*x1+h8_lm*y1+h9_lm);
dx_lm = x_Cord_est- f1_est_lm ;
dy_lm = y_Cord_est- f2_est_lm;
d_lm = cat(1,dx_lm ,dy_lm );
e_lm=dot(d_lm,d_lm);
if e_lm
优化后结果