【Week 14 作业】A - Q老师与石头剪刀布（必做）、B - Q老师与十字叉（必做）、C - Q老师的考验（必做）、D - Q老师染砖（选做）、E - Q老师度假（选做）

A - Q老师与石头剪刀布（必做）

题意：

每一个大人曾经都是一个小孩，Q老师 也一样。

为了回忆童年，Q老师 和 Monika 玩起了石头剪刀布的游戏，游戏一共 n 轮。无所不知的 Q老师 知道每一轮 Monika 的出招，然而作为限制， Q老师 在这 n 轮游戏中必须恰好出 a 次石头，b 次布和 c 次剪刀。

如果 Q老师 赢了 Monika n/2(上取整) 次，那么 Q老师就赢得了这场游戏，否则 Q老师 就输啦！

Q老师非常想赢，他想知道能否可以赢得这场游戏，如果可以的话，Q老师希望你能告诉他一种可以赢的出招顺序，任意一种都可以。

Input

第一行一个整数 t(1 ≤ t ≤ 100)表示测试数据组数。然后接下来的 t 组数据，每一组都有三个整数：

第一行一个整数 n(1 ≤ n ≤ 100)
第二行包含三个整数 a, b, c(0 ≤ a, b, c ≤ n)。保证 a+b+c=n
第三行包含一个长度为 n 的字符串 s，字符串 s 由且仅由 ‘R’, ‘P’, ‘S’ 这三个字母组成。第 i 个字母 s[i] 表示 Monika 在第 i 轮的出招。字母 ‘R’ 表示石头，字母 ‘P’ 表示布，字母 ‘S’ 表示剪刀

Output

对于每组数据：

如果 Q老师 不能赢，则在第一行输出 “NO”(不含引号)
否则在第一行输出 “YES”(不含引号)，在第二行输出 Q老师 的出招序列 t。要求 t 的长度为 n 且仅由 ‘R’, ‘P’, ‘S’ 这三个字母构成。t 中需要正好包含 a 个 ‘R’，b 个 ‘P’ 和 c 个 ‘S’
“YES”/"NO"是大小写不敏感的，但是 ‘R’, ‘P’, ‘S’ 是大小写敏感的。

Sample Input

2
3
1 1 1
RPS
3
3 0 0
RPS

Sample Output

YES
PSR
NO

思路做法：

统计对手的出招，计算最多可能的胜场数量，若没有超过一半，输出NO结束，否则，统计己方出招，将多出来的赢不了的出招匀到其他地方，按顺序打印即可。

总结:

遇到类似题目不要嫌麻烦，即便代码可能很多，但是考虑了所有情况还是很简单的。

代码:

#include 
#include 
#include 
#include 
using namespace std;
map<char, int> zh, cnt;
char seq[120];
int main(){
	int t; scanf("%d", &t);
	while(t--){
		zh.clear();
		int n; scanf("%d", &n);
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		getchar();
		for(int i = 0; i < n; ++i){
			scanf("%c", &seq[i]);
			zh[seq[i]]++;
		}
		int ans = 0;
		int _a = 0, _b = 0, _c = 0;
//		printf("a=%d, b=%d, c=%d, aa=%d, bb=%d, cc=%d\n", a, b, c, zh['R'], zh['P'], zh['S']);
		if(a <= zh['S']){
			ans += a;
		}else{
			ans += zh['S']; _a = a - zh['S'];
		}
		if(b <= zh['R']){
			ans += b;
		}else{
			ans += zh['R']; _b = b - zh['R'];
		}
		if(c <= zh['P']){
			ans += c;
		}else{
			ans += zh['P']; _c = c - zh['P'];
		}
		if(n%2==1 && ans<=n/2 || n%2==0 && ans<n/2) printf("NO\n");
		else{
			printf("YES\n");  // 能赢 
			for(int i = 0; i < n; ++i){
				if(seq[i] == 'R'){
					if(b > 0){
						b--; printf("P");
					}else{
						if(_a > 0){
							_a--; printf("R");
						}else if(_c > 0){
							_c--; printf("S");
						}
					}
				}
				if(seq[i] == 'P'){
					if(c > 0){
						c--; printf("S");
					}else{
						if(_a > 0){
							_a--; printf("R");
						}else if(_b > 0){
							_b--; printf("P");
						}
					}
				}
				if(seq[i] == 'S'){
					if(a > 0){
						a--; printf("R");
					}else{
						if(_b > 0){
							_b--; printf("P");
						}else if(_c  > 0){
							_c--; printf("S");
						}
					}
				}
			}
			printf("\n");
		}
	}
	return 0;
}

B - Q老师与十字叉（必做）

题意：

Q老师 得到一张 n 行 m 列的网格图，上面每一个格子要么是白色的要么是黑色的。

Q老师认为失去了 十字叉 的网格图莫得灵魂. 一个十字叉可以用一个数对 x 和 y 来表示, 其中 1 ≤ x ≤ n 并且 1 ≤ y ≤ m, 满足在第 x 行中的所有格子以及在第 y 列的 所有格子都是黑色的

例如下面这5个网格图里都包含十字叉

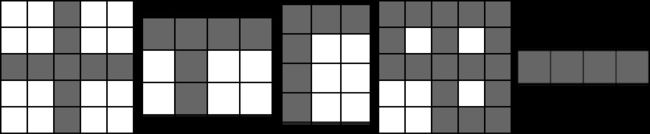
第四个图有四个十字叉，分别在 (1, 3), (1, 5), (3, 3) 和 (3, 5).
下面的图里没有十字叉

Q老师 得到了一桶黑颜料，他想为这个网格图注入灵魂。 Q老师 每分钟可以选择一个白色的格子并且把它涂黑。现在他想知道要完成这个工作，最少需要几分钟？

Input

第一行包含一个整数 q (1 ≤ q ≤ 5 * 10^4) — 表示测试组数

对于每组数据：
第一行有两个整数 n 和 m (1 ≤ n, m ≤ 5 * 10^4, n * m ≤ 4 * 10^5) — 表示网格图的行数和列数

接下来的 n 行中每一行包含 m 个字符 — ‘.’ 表示这个格子是白色的， ‘*’ 表示这个格子是黑色的

保证 q 组数据中 n 的总和不超过 5 * 10^4， n*m 的总和不超过 4 * 10^5

Output

答案输出 q 行, 第 i 行包含一个整数 — 表示第 i 组数据的答案

Sample Input

9
5 5
..*..
..*..
*****
..*..
..*..
3 4
****
.*..
.*..
4 3
***
*..
*..
*..
5 5
*****
*.*.*
*****
..*.*
..***
1 4
****
5 5
.....
..*..
.***.
..*..
.....
5 3
...
.*.
.*.
***
.*.
3 3
.*.
*.*
.*.
4 4
*.**
....
*.**
*.**

Sample Output

0
0
0
0
0
4
1
1
2

思路做法：

输入整个字符数组时，记录每行和每列的黑格数量。输入完再遍历一遍，计算最小的cost。注意一点：每行和每列的黑格数量可能存在重复的记录，更新答案时要判断一下。
当cost为0时代表存在十字架，可以break提前退出。

总结:

一开始没做出来是因为高估了复杂度，以为数据最大是4e5*5e4,而不能用遍历的方法，但是又想不出其他方法。
开辟二维数组时开的太大，可以改成一维数组，空间消耗会大幅降低，而代码基本不变。

代码:

#include 
const int N = 4e5+20;
const int M = 5e4+20;
char gezi[N];
int hang[M], lie[M];
int main(){
	int q; scanf("%d", &q);
	while(q--){
		int n, m; scanf("%d%d", &n, &m);
		for(int i = 1; i <= n; ++i) hang[i] = 0;
		for(int j = 1; j <= m; ++j) lie[j] = 0;
		for(int i = 1; i <= n; ++i){
			getchar();
			for(int j = 1; j <= m; ++j){
				scanf("%c", &gezi[i*m+j]);
				if(gezi[i*m+j] == '*'){
					hang[i]++; lie[j]++;
				}
			}
		}
		int ans = 1e9;
		for(int i = 1; i <= n; ++i){
			for(int j = 1; j <= m; ++j){
				int cost = m-hang[i]+n-lie[j];
				if(gezi[i*m+j] == '.') cost--;
				if(cost < ans) ans = cost;
				if(cost == 0) break;
			}
		}
		printf("%d\n", ans);
	}
	return 0;
}

C - Q老师的考验（必做）

题意：

Q老师 对数列有一种非同一般的热爱，尤其是优美的斐波那契数列。

这一天，Q老师 为了增强大家对于斐波那契数列的理解，决定在斐波那契的基础上创建一个新的数列 f(x) 来考一考大家。数列 f(x) 定义如下：

当 x < 10 时，f(x) = x；
当 x ≥ 10 时，f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10)，ai 只能为 0 或 1。

Q老师 将给定 a0～a9，以及两个正整数 k m，询问 f(k) % m 的数值大小。

聪明的你能通过 Q老师 的考验吗？

Input

输出文件包含多组测试用例，每组测试用例格式如下：

第一行给定两个正整数 k m。（k < 2e9, m < 1e5）

第二行给定十个整数，分别表示 a0～a9。

Output

对于每一组测试用例输出一行，表示 f(k) % m 的数值大小。

Sample Input

10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0

Sample Output

45
104

思路做法：

O(n)的复杂度会超时，因此采用矩阵快速幂。
将给出的新斐波那契数列转化成矩阵乘向量的形式，然后就可以应用矩阵快速幂，以O(logn)的复杂度计算出最终矩阵，再和初始条件向量相乘即可。

总结:

类似的题目都可以尝试将原式转化成矩阵形式应用矩阵快速幂来优化复杂度。

代码:

#include 
/*
f(x)=x  x<10
f(x)      a0 a1 a2 a3 a4 a5 a6 a7 a8 a9  f(x-1)
f(x-1)     1  0  0  0  0  0  0  0  0  0  f(x-2)

       =

f(x-9)     0  0  0  0  0  0  0  0  1  0  f(x-10)
*/
struct Matrix{
	int b[15][15];
	Matrix(){}
	Matrix(int *c){
		for(int i = 0; i < 10; ++i){
			b[0][i] = c[i];
		}
		for(int i = 1; i < 10; ++i){
			for(int j = 0; j < 10; ++j){
				if(i-1 == j) b[i][j] = 1;
				else b[i][j] = 0;
			}
		}
	}
	Matrix operator*(const Matrix& m){
		Matrix mat;
		for(int i = 0; i < 10; ++i){
			for(int j = 0; j < 10; ++j){
				mat.b[i][j] = 0;
				for(int k = 0; k < 10; ++k){
					mat.b[i][j] += (b[i][k]*m.b[k][j]);
				}
			}
		}
		return mat;
	}
	Matrix operator%(int m){
		for(int i = 0; i < 10; ++i){
			for(int j = 0; j < 10; ++j){
				b[i][j] %= m;
			}
		}
		return *this;
	}
	void output(){
		for(int i = 0; i < 10; ++i){
			for(int j = 0; j < 10; ++j){
				printf("%d ", b[i][j]);
			}
			printf("\n");
		}
	}
};
Matrix quick_pow(Matrix m, int x, int mod){
	Matrix mat;
	for(int i = 0; i < 10; ++i){
		for(int j = 0; j < 10; ++j){
			if(i == j) mat.b[i][j] = 1;
			else mat.b[i][j] = 0;
		}
	}
	while(x){
		if(x & 1) mat = mat * m % mod;
		m = m * m % mod;
		x >>= 1;
	}
	return mat;
}
int a[15];
int main(){
	int k, m;
	while(~scanf("%d%d", &k, &m)){
		for(int i = 0; i < 10; ++i) scanf("%d", &a[i]);
		Matrix mat(a);
//		mat.output();
		if(k < 10) printf("%d\n", k % m);
		else{
			Matrix d = quick_pow(mat, k-9, m);
//			d.output();
			int ans = 0;
			for(int i = 0; i < 10; ++i){
				ans += d.b[0][i]*(9-i);
			}
			printf("%d\n", ans % m);
		}
	}
	return 0;
}

D - Q老师染砖（选做）

题意：

衣食无忧的 Q老师 有一天突发奇想，想要去感受一下劳动人民的艰苦生活。

具体工作是这样的，有 N 块砖排成一排染色，每一块砖需要涂上红、蓝、绿、黄这 4 种颜色中的其中 1 种。且当这 N 块砖中红色和绿色的块数均为偶数时，染色效果最佳。

为了使工作效率更高，Q老师 想要知道一共有多少种方案可以使染色效果最佳，你能帮帮他吗？

Input

第一行为 T，代表数据组数。(1 ≤ T ≤ 100)

接下来 T 行每行包括一个数字 N，代表有 N 块砖。(1 ≤ N ≤ 1e9)

Output

输出满足条件的方案数，答案模 10007。

Sample Input

2
1
2

Sample Output

2
6

思路做法：

动态规划问题，定义单独的1个状态不够，要定义3个a，b，c，分别代表红绿均偶数、红绿均奇数、红绿一奇一偶的情况下使染色效果最佳的方案数。接着找转移方程，即
$a[i]=2\ast a[i-1]+c[i-1]$
$b[i]=2\ast b[i-1]+c[i-1]$
$c[i]=2\ast a[i-1]+2\ast b[i-1]+2\ast c[i-1]$
如果循环转移的话复杂度会超，因此将3个状态转移方程转化成矩阵乘向量形式，用矩阵快速幂优化。

总结:

题目是一个动态规划问题，只不过要用矩阵快速幂优化复杂度。

代码:

#include 
/*
DP: a[i]红绿均偶数  b[i]红绿均奇数  c[i]红绿一奇一偶
a[i]  2*a[i-1]+c[i-1]            2 0 1    a[i-1] a[1] = 2
b[i]  2*b[i-1]+c[i-1]            0 2 1    b[i-1] b[1] = 0
c[i]  2*a[i-1]+2*b[i-1]+2*c[i-1] 2 2 2    c[i-1] c[1] = 2
*/
const int sz = 3;
struct Matrix{
	int b[sz+2][sz+2];
	Matrix(){
		b[0][0] = 2; b[0][1] = 0; b[0][2] = 1;
		b[1][0] = 0; b[1][1] = 2; b[1][2] = 1;
		b[2][0] = 2; b[2][1] = 2; b[2][2] = 2;
	}
	Matrix operator*(const Matrix& m){
		Matrix mat;
		for(int i = 0; i < sz; ++i){
			for(int j = 0; j < sz; ++j){
				mat.b[i][j] = 0;
				for(int k = 0; k < sz; ++k){
					mat.b[i][j] += (b[i][k]*m.b[k][j]);
				}
			}
		}
		return mat;
	}
	Matrix operator%(int m){
		for(int i = 0; i < sz; ++i){
			for(int j = 0; j < sz; ++j){
				b[i][j] %= m;
			}
		}
		return *this;
	}
	void output(){
		for(int i = 0; i < sz; ++i){
			for(int j = 0; j < sz; ++j){
				printf("%d ", b[i][j]);
			}
			printf("\n");
		}
	}
};
Matrix quick_pow(Matrix m, int x, int mod){
	Matrix mat;
	for(int i = 0; i < sz; ++i){
		for(int j = 0; j < sz; ++j){
			if(i == j) mat.b[i][j] = 1;
			else mat.b[i][j] = 0;
		}
	}
	while(x){
		if(x & 1) mat = mat * m % mod;
		m = m * m % mod;
		x >>= 1;
	}
	return mat;
}
int main(){
	int t; scanf("%d", &t);
	while(t--){
		int n; scanf("%d", &n);
		int mod = 10007;
		Matrix m;
		if(n == 1) printf("%d\n", 2 % mod);
		else{
			Matrix mat = quick_pow(m, n-1, mod);
			int ans = mat.b[0][0]*2%mod+mat.b[0][2]*2%mod;
			printf("%d\n", ans % mod);
		}
	}
	return 0;
}

E - Q老师度假（选做）

题意：

忙碌了一个学期的 Q老师 决定奖励自己 N 天假期。

假期中不同的穿衣方式会有不同的快乐值。

已知 Q老师 一共有 M 件衬衫，且如果昨天穿的是衬衫 A，今天穿的是衬衫 B，则 Q老师 今天可以获得 f[A][B] 快乐值。

在 N 天假期结束后，Q老师 最多可以获得多少快乐值？

Input

输入文件包含多组测试样例，每组测试样例格式描述如下：

第一行给出两个整数 N M，分别代表假期长度与 Q老师 的衬衫总数。（2 ≤ N ≤ 100000, 1 ≤ M ≤ 100）

接下来 M 行，每行给出 M 个整数，其中第 i 行的第 j 个整数，表示 f[i][j]。（1 ≤ f[i][j] ≤ 1000000）

测试样例组数不会超过 10。

Output

每组测试样例输出一行，表示 Q老师 可以获得的最大快乐值。

Sample Input

3 2
0 1
1 0
4 3
1 2 3
1 2 3
1 2 3

Sample Output

2
9

思路做法：

动态规划问题，定义状态$dp[i][j]$为第i天穿第j件衣服可以得到的最大总快乐值。可以遍历每件衣服，即
$dp[i][j]=max(dp[i-1][k]+f[k][j])$
用矩阵快速幂优化复杂度，这里的矩阵相乘需要修改一下，将乘法换为加法，将加法换为取最大值，由于符合结合律，因此可以这样修改。dp数组初始化为f数组中每一列的最大值。另外矩阵快速幂也要修改，初始矩阵不再是单位矩阵。

总结:

答案可能溢出int，将所有值的类型都改成long long即可
dp数组没必要开很多个，因为用矩阵快速幂可以直接求得最终矩阵，因此开2个dp数组即可。

代码:

#include 
#include 
using namespace std;
#define ll long long
/*
DP:dp[i][j]  max(dp[i-1][k]+f[k][j])  N*M*M  1e9
dp[2][i] = max(f[k][i])
dp[i][1]  f[1][1]  f[2][1]     f[M][1]   dp[i-1][1]


dp[i][M]  f[1][M]  f[2][M]     f[M][M]   dp[i-1][M]
*/
const int M = 1e2+20;
const int N = 1e5+20;
ll f[M][M], dp2[M], dpn[M];
int n, m;
struct Matrix{
	ll a[M][M];
	Matrix(){
		for(int i = 1; i <= m; ++i){
			for(int j = 1; j <= m; ++j){
				a[i][j] = f[j][i];
			}
		}	
	}
	Matrix operator*(const Matrix& mat){
		Matrix ans;
		for(int i = 1; i <= m; ++i){
			for(int j = 1; j <= m; ++j){
				ans.a[i][j] = 0;
				for(int k = 1; k <= m; ++k){
					ans.a[i][j] = max(ans.a[i][j], a[i][k]+mat.a[k][j]);
				}
			}
		}
		return ans;
	}
	void output(){
		for(int i = 1; i <= m; ++i){
			for(int j = 1; j <= m; ++j){
				printf("%lld ", a[i][j]);
			}
			printf("\n");
		}
	}
};
Matrix quick_pow(Matrix mat, int x){
	Matrix ans;
	bool f = 1;
	while(x){
		if(x & 1){
			if(f){
				ans = mat; f = 0;
			}
			else ans = ans * mat;
		}
		mat = mat * mat;
		x >>= 1;
	}
	return ans;
}
int main(){
	while(~scanf("%d%d", &n, &m)){
		for(int i = 1; i <= m; ++i)
			for(int j = 1; j <= m; ++j)
				scanf("%lld", &f[i][j]);
		for(int j = 1; j <= m; ++j){
			dp2[j] = 0;
			for(int i = 1; i <= m; ++i){
				if(f[j][i] > dp2[j]) dp2[j] = f[j][i];
			}
		}
		Matrix mat;
		ll ans = 0;
		if(n == 2){
			for(int i = 1; i <= m; ++i){
				if(dp2[i] > ans) ans = dp2[i];
			}
			printf("%lld\n", ans);
		}else{
			Matrix b = quick_pow(mat, n-2);
//			b.output();
			for(int i = 1; i <= m; ++i){
				dpn[i] = 0;
				for(int j = 1; j <= m; ++j){
					dpn[i] = max(dpn[i], b.a[j][i]+dp2[j]);
				}
			}
			for(int i = 1; i <= m; ++i){
				ans = max(ans, dpn[i]);
			}
			printf("%lld\n", ans);
		}
	}
	return 0;
}