【CNN基础】局部响应归一化、gated convolution和gated deconv

〇、 参考文献

1. 论文来源：
   Yu J, Lin Z, Yang J, et al. Free-form image inpainting with gated convolution[J]. arXiv preprint arXiv:1806.03589, 2018. DeepFillv2-code
   Jo Y, Park J. SC-FEGAN: Face Editing Generative Adversarial Network with User’s Sketch and Color[J]. arXiv preprint arXiv:1902.06838, 2019. SC-FEGAN-code
2. 相关博客：
   论文阅读之《Image Inpainting for Irregular Holes Using Partial Convolutions》

---

一、gated conv的引入

1. gated conv 解决什么问题？

the proposed gated convolution solves the issue of vanilla convolution that treats all input pixels as valid ones, generalizes partial convolution by providing a learnable dynamic feature selection mechanism for each channel at each spatial location across all layers.

1. vanilla convolution(普通卷积)认为所有通道的输入像素都是有效的，但gated convolution可以通过对每个channel应用参数可学的特征选择机制，将所有层响应空间位置的像素融合到一起，达到对partial convolution(部分卷积)进行泛化的目的。
2. 针对规则的矩形mask设计出来的GANs无法处理free-form masks，已经有文章论证了vanilla convolution无法解决free-form image inpainting任务。Iizuka et al.2017、Yu et al. 2018

---

2. vanilla conv 为什么无效？

对于free-form image inpainting任务，vanilla conv是无效

       ~~~~~~       首先来看vanilla conv的公式：$$O_{y,x}=\sum _{i=-k_h^{{}^{\prime }}}^{k_h^{{}^{\prime }}}\sum _{i=-k_w^{{}^{\prime }}}^{k_w^{{}^{\prime }}}{W}_{k_h^{{}^{\prime }}+i,k_w^{{}^{\prime }}+j}\cdot I_{y+i,x+j}$$        ~~~~~~       对于输入图像I的每个通道的坐标点位置$I_{x,y}$，都会有相同形态的滤波器（这里指kernel size，非每个滤波器本身的系数）对其进行vanilla conv操作。这对于classificaton和object detection任务是有意义的，因为每一个输入像素对于通过滑窗方式提取local feature都是有效的，即: vanilla conv对每个输入像素使用相同形态但系数不同的滤波器，可以有效地提取出图像的local feature。
       ~~~~~~        然而，对于image inpainting任务，input feature由valid pixels outside holes、invalid pixels in the masked regions（这些像素通常指在shallow layers才有，因为随着层数变深，invalid pixel会逐渐变成valid pixel）或synthesized pixels in the masked regions (deep layers)组成，这会使训练产生ambiguity，导致测试阶段产生visual artifacts，比如color discrepancy，blurriness，obvious edge responses。

---

3. partial conv如何解决ambiguity？

partial conv的mask-update应该是以滑窗为单元，更新策略应该类似于腐蚀操作，随着层数增加，mask的黑色条纹应该会越来越细，图3的示意图可以印证这个观点。更多细节就需要阅读源码。

       ~~~~~~       为了让卷积只依赖于valid pixel，partial conv提出了masking和re-normalization策略，partial conv的公式如下：$$O_{y,x}=\{\begin{array}{cc}\sum \sum W\cdot \left(I\odot \frac{M}{sum\left(M\right))}\right)& ifsum\left(M\right)>0\\ 0& otherwise\end{array}$$
       ~~~~~~       其中M是对应的binary mask，每次经过partial conv，mask-update遵循以下策略：$$m_{y,x}^{{}^{\prime }}=\{\begin{array}{cc}1& ifsum\left(M\right)>0\\ 0& otherwise\end{array}$$
       ~~~~~~       partial conv的确提升了inpainting任务在irregular masks上的表现，但仍有以下几点缺陷：

1. 它只是启发式地将所有空间像素分成valid和invalid两种。不论有多少个像素被前一层的滤波器覆盖，下一层的mask都会被设置为Ones(即1 valid pixel和9 valid pixels对于更新当前mask是无差别的)
2. 它对于额外的用户输入不兼容。例如user-guided image inmpainting system可以允许用户在mask内部画一些素描作为条件属性，这些素描像素点究竟是valid，还是invalid呢？下一层的mask又该如何更新才好呢？
   
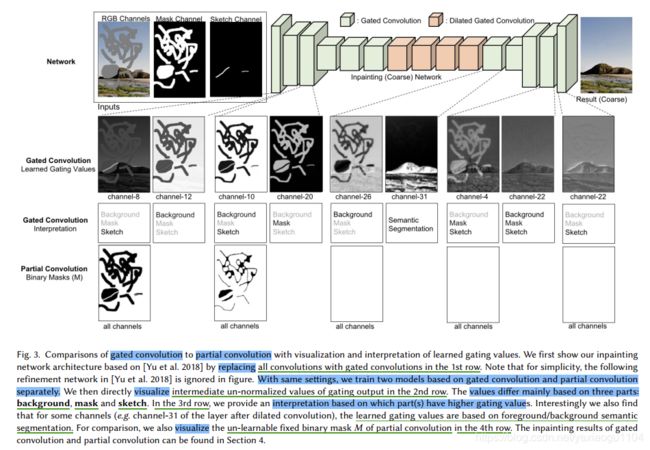
3. 随着层的加深，invalid pixels（mask中的黑色部分）会逐渐消失，mask的所有像素值会慢慢地都变成1，如图3: row-4所示。而gated conv的研究表明，如果让网络自己去学习最佳的mask，网络会给mask的每个空间位置学习到soft mask value（图3: row-2）。即partial conv不如gated conv合理的。
4. 每一层的所有channel都共享同一个mask，限制了网络的flexibility。
   

---

4. 什么是gated conv

partial conv可以被认为是hard-gating single-channel un-learnable layer再跟input feature map逐像素点乘。

       ~~~~~~       gated conv抛弃通过固定规则进行更新的hard mask，而是从数据中自动学习soft mask，公式如下：$$Gatin{g}_{y,x}=\sum \sum W_g\cdot I$$$$Featur{e}_{y,x}=\sum \sum W_f\cdot I$$$$O_{y,x}=\varphi \left(Featur{e}_{y,x}\right)\odot \sigma \left(Gatin{g}_{y,x}\right)$$
       ~~~~~~       其中，$\sigma$表示对0～1的output gating values使用sigmoid激活函数，$\varphi$可以是任意激活函数（ReLU or LeakyReLU）

       ~~~~~~       gated conv使得网络可以针对每个channel和每个空间位置，学习一种动态特征选择机制。有趣的是，图3: row-3的intermediate gating value可视化表明，网络不仅可以根据background、mask和sketch，也可以根据一些通道的semantic segmentation来选择feature maps。甚至在更深的层，gated conv可以在不同的channel对masked regions进行highlight ，也可以sketch必要的information，来获得更好的inpainting结果。

---

二、效果展示

客观指标：mean L1 loss, mean L2 loss, mean TV loss
主观效果

1. DeepFillv2主观效果

• 观察眉毛部分，partial conv可以恢复出皮肤的纹理和颜色，但是黑色线条对应的眉毛却没恢复出来，根据之前“partial conv的mask-update类似于腐蚀操作”的分析，mask当中的黑色线条会越来越细，最终全部变成白色，眉毛还没恢复出来，mask就已经失效了。
• gated conv则可以拟合并恢复出mask中的黑色线条对应的眉毛，这说明soft mask起了作用。
  

---

三、代码实现

实现参考：SC-FEGAN

1. Local response normalization（局部响应归一化）

1. 局部响应归一化，由于做了平滑处理，可以增加泛化能力，公式如下
   $$b_{x,y}^i=a_{x,y}^i/\left(bias+\alpha \sum _{j=\max (0,i-n/2)}^{\min (N-1,i+n/2)}{(a_{x,y}^i)}^2\right)$$
   其中i代表在第几个feature map，(x,y)代表所在feature map位置
2. tensorflow有内置函数tf.nn.lrn，参数输入与解释如下

"""Local Response Normalization.

  The 4-D `input` tensor is treated as a 3-D array of 1-D vectors (along the last
  dimension), and each vector is normalized independently.  Within a given vector,
  each component is divided by the weighted, squared sum of inputs within
  `depth_radius`.  In detail,

      sqr_sum[a, b, c, d] =
          sum(input[a, b, c, d - depth_radius : d + depth_radius + 1] ** 2)
      output = input / (bias + alpha * sqr_sum) ** beta
  a is batch size. d is channel.

2. gated convolution

       ~~~~~~       公式如下
$$y(\mathbf{X})=(\mathbf{X}\ast \mathbf{W}+\mathbf{b})\otimes \sigma (\mathbf{X}\ast \mathbf{V}+\mathbf{c})$$
       ~~~~~~       其中 W，V为两个不同的卷积核
       ~~~~~~       tensorflow实现方法如下

def gate_conv(x_in, cnum, ksize, stride=1, rate=1, name='conv',
              padding='SAME', activation='leaky_relu', use_lrn=True, training=True):
    assert padding in ['SYMMETRIC', 'SAME', 'REFELECT']
    if padding == 'SYMMETRIC' or padding == 'REFELECT':
        p = int(rate * (ksize - 1) / 2)
        x = tf.pad(x_in, [[0, 0], [p, p], [p, p], [0, 0]], mode=padding)
        padding = 'VALID'
    x = tf.layers.conv2d(
        x_in, cnum, ksize, stride, dilation_rate=rate,
        activation=None, padding=padding, name=name)
    if use_lrn:
        x = tf.nn.lrn(x, bias=0.00005)
    if activation == 'leaky_relu':
        x = tf.nn.leaky_relu(x)

    g = tf.layers.conv2d(
        x_in, cnum, ksize, stride, dilation_rate=rate,
        activation=tf.nn.sigmoid, padding=padding, name=name + '_g')

    x = tf.multiply(x, g)
    return x, g

3. gated deconvolution

def gate_deconv(input_, output_shape, k_h=5, k_w=5, d_h=2, d_w=2, stddev=0.02,
       name="deconv", training=True):
    with tf.variable_scope(name):
        # filter : [height, width, output_channels, in_channels]
        w = tf.get_variable('w', [k_h, k_w, output_shape[-1], input_.get_shape()[-1]],
                  initializer=tf.random_normal_initializer(stddev=stddev))

        deconv = tf.nn.conv2d_transpose(input_, w, output_shape=output_shape,
                    strides=[1, d_h, d_w, 1])

        biases = tf.get_variable('biases1', [output_shape[-1]], initializer=tf.constant_initializer(0.0))
        deconv = tf.reshape(tf.nn.bias_add(deconv, biases), deconv.get_shape())
        deconv = tf.nn.leaky_relu(deconv)

        g = tf.nn.conv2d_transpose(input_, w, output_shape=output_shape,
                    strides=[1, d_h, d_w, 1])
        b = tf.get_variable('biases2', [output_shape[-1]], initializer=tf.constant_initializer(0.0))
        g = tf.reshape(tf.nn.bias_add(g, b), deconv.get_shape())
        g = tf.nn.sigmoid(deconv)

        deconv = tf.multiply(g,deconv)

        return deconv, g