本文不允许任何形式的转载!
阅读提示
本系列文章不适合以下人群阅读,如果你无意点开此文,请对号入座,避免浪费你宝贵的时间。
- 想要学习利用游戏引擎开发游戏的朋友。本文不会涉及任何第三方游戏引擎。
- 不具备面向对象编程经验的朋友。本文的语言主要是Javascript(ECMA 2016),如果你不具备JS编程经验倒也无妨,但没有面向对象程序语言经验就不好办了。
- 想要直接下载实例代码的朋友。抱歉,我都用嘴说,基本上没有示例代码。
上期作业
如何用moveTo,lineTo,beginPath和closePath去实现arc接口呢?其实不难,只要我们能计算出弧形上的点的位置,然后一个一个连接他们就好了,代码如下:
function arc(x, y, r, startAngel, endAngel) {
if (startAngel == endAngel) return; // 如果弧度是没变化的,画尼玛
let plusRadian = 0.01; // 我们固定一个增量为0.01
if (startAngel > endAngel) { // 如果弧度递减绘制点的,那plusRadian为负数
plusRadian *= -1;
}
let startPoint = getPointOnArc(x, y, r, startAngel);
ctx.moveTo(startPoint.x, startPoint.y);
for (let radian = startAngel + plusRadian; condition(radian); radian += plusRadian) {
let nextPoint = getPointOnArc(x, y, r, radian);
ctx.lineTo(nextPoint.x, nextPoint.y);
// 如果增量转了一圈,就退出没必要再绘制了
if (Math.abs(radian) >= 2 * Math.PI) {
break;
}
}
function getPointOnArc(x, y, r, radian) {
let x1 = x + r * Math.cos(radian);
let y1 = y + r * Math.sin(radian);
return {x: x1, y: y1}
}
function condition(radian) {
if (plusRadian > 0) {
return radian < endAngel;
}
if (plusRadian < 0) {
return radian > endAngel;
}
}
}
这样写出来是可以实现的,但是需要的点都是固定的,设想一下,一个半径只有1的圆,我们真的不需要这么多个点来围城一个弧形,几个就够了;反之如果半径非常大,那仅仅增加0.01个弧度是无法绘制出一个弧线的,所以增量不能固定,需要配合半径进行计算,如下图所示:
那上面那个程序的plusRadian就可以改成:
let plusRadian = Math.asin(0.5 / r)*2; // 这次我们将这个增量通过半径算出来
这样一来,就算完成了arc方法了(如果有bug自行修改)。那真就完成了么?不是的,我们在本文最后再说一下这个问题。
Context状态
所谓状态就好像我们画画的时候所用的笔以及纸的不同状态,例如,我要画一个太阳,起初拿了一根红色笔画出太阳的圆圈,然后我换成了黄色的笔来涂画圆形内部,那么我可以认为目前我画了这个太阳用到了两种不同状态的笔:红色很黄色。
展开来想,笔的状态不仅仅是颜色的不同,还有笔芯的粗细啦等等。
而什么是纸的状态呢。我们画画的时候,经常是手压住纸,手是要在纸上来回找位置绘制,但也有时会把纸挪动一下位置便于我们画图,例如我要在刚才的太阳下面画一座小山,那我会在画好太阳后把纸往上移动,我的手就懒得挪动太远去画那座山了。
在CanvasRenderingContext2D中(下面统称ctx),有一种东西叫做状态,就是来实现刚才我说的那些,比如画笔颜色,可以用strokeStyle和fillStyle进行设置,笔芯的粗细可以用lineWidth来设置,移动纸张可以用translate来设置,等等。
现在来说说ctx里的状态有哪些。如果我们按照刚才所说的,把ctx的常用状态看成笔和纸,大致可以分成:
画笔状态:
颜色 : fillStyle, strokeStyle
透明度 :globalAlpha
线条宽度:lineWidth
.....
坐标变换状态:移动位置:translate
旋转:rotate
缩放:scale
画笔状态很好理解,上一节就用到过,我们现在举个例子,快速搞清楚上面说的位置变化状态。
Context的translate
现在我要画一组图形,是两个宽高为50像素正方形的方块,方块2的左上角在方块1的中心,代码可以这么写:
let ctx = main.getContext('2d');
ctx.fillStyle = 'black';
drawRect(0,0,50,50); // 左上角坐标在0,0处,宽高为50的正方形
// 左上角坐标在上个正方的中心,也就是(25,25)的一个正方形
drawRect(25,25,50,50);
function drawRect(x, y, width, height) {
ctx.beginPath();
ctx.rect(x, y, width, height);
ctx.closePath();
ctx.fill()
}
上面这个段代码,我们可以想象成:用笔在0,0点画了一个正方形,然后我拿起笔移动到这个正方形的中心位置再画一个正方形。如果我手不动,而是纸动呢,结合上面所提到的ctx的translate方法,代码改为:
let ctx = main.getContext('2d');
ctx.fillStyle = 'black';
drawRect(0,0,50,50); // 在左上角(0,0)绘制一个50x50的正方形
ctx.translate(25,25); // 变换绘制坐标(移动纸张)
drawRect(0,0,50,50); // 在新的坐标系的(0,0)绘制一个50x50的正方形
function drawRect(x, y, width, height) {
ctx.beginPath();
ctx.rect(x, y, width, height);
ctx.closePath();
ctx.fill()
}
这两段代码得到的结果是一样的,但是理解起来就不一样了。第一段代码是我们在不同的坐标点绘制正方形,而第二段代码我们绘制的正方形左上角坐标都是(0,0),只是在绘制第二个的时候,ctx的坐标系发生了变化,就好像我在画画,刚画好一个正方形,然后我把纸挪动了,但是我的手并没有动,继续在刚才绘制正方形的地方再画一个。 通常来讲,计算机二维图形的坐标系是以左上角作为原点,x轴往右递增,y轴往下递增。ctx的坐标系也是如此,在一开始,ctx的坐标系也是以canvas的左上角作为原点的,一旦我们调用了ctx.translate方法,就能更改这个坐标系的原点(想象一下我们挪动纸张画画的情景)。
Context的rotate
这个很重要,希望能认真看
先看代码:
let ctx = main.getContext('2d');
ctx.fillStyle = 'black';
ctx.rotate(45*Math.PI/180); // 旋转45度
drawRect(0,0,50,50);
function drawRect(x, y, width, height) {
ctx.beginPath();
ctx.rect(x, y, width, height);
ctx.closePath();
ctx.fill()
}
我们在绘制刚才第一个方块的之前调用了rotate方法,那得到的结果是这样的:
我们看到,整个方块发生了旋转,但因为我们的canvas大小原因只显示了一半。
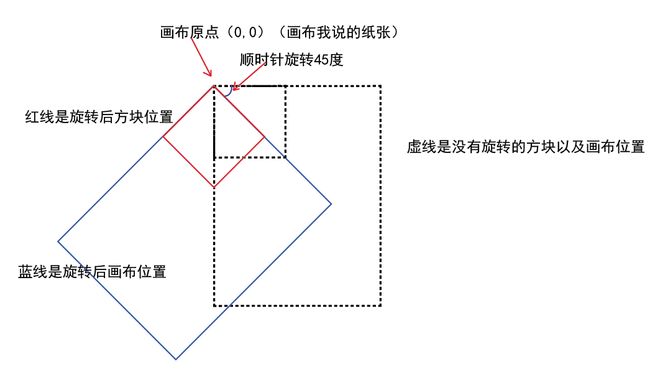
我们知道,旋转一个物体是需要有几个前提,一个是该物体要基于哪个点进行旋转,二是旋转的弧度以及方向,上述的这次旋转是以哪个点转的呢?旋转方向又是什么?我们画个图就能理解了。
ctx里,所有旋转都是基于当前画布的原点,我们上述代码中,rotate 45度,就是基于画布的原点旋转的,而且该原点并没有发生变化,依旧是【0,0】。
而旋转方向的规则是这样的:以x轴往右作为方向,如果旋转角度是大于0的,则顺时针旋转;如果旋转角度小于0,则逆时针旋转。
旋转方向还好理解,也好更改,那旋转点怎么改呢?就是我们上一小节提到的translate(退回去看看)。例如,我们在旋转之前将原点改到(25,25)会怎样呢
let ctx = main.getContext('2d');
ctx.fillStyle = 'black';
ctx.translate(25,25);
ctx.rotate(45*Math.PI/180);
drawRect(0,0,50,50);
function drawRect(x, y, width, height) {
ctx.beginPath();
ctx.rect(x, y, width, height);
ctx.closePath();
ctx.fill()
}
我们可以看到,这个方块旋转还是那样旋转的,只是位置改了,如图所示:
好了,现在知道怎么改旋转原点和怎么进行旋转了,那我们考虑一下这个case: 我想让方块基于它的中心点旋转45度,怎么办。先看代码:
let ctx = main.getContext('2d');
ctx.fillStyle = 'black';
ctx.translate(25,25);
ctx.rotate(45*Math.PI/180);
ctx.translate(-25,-25);
drawRect(0,0,50,50);
function drawRect(x, y, width, height) {
ctx.beginPath();
ctx.rect(x, y, width, height);
ctx.closePath();
ctx.fill()
}
可以看到,ctx的位置变化是这样的:
ctx.translate(25,25);
ctx.rotate(45*Math.PI/180);
ctx.translate(-25,-25);
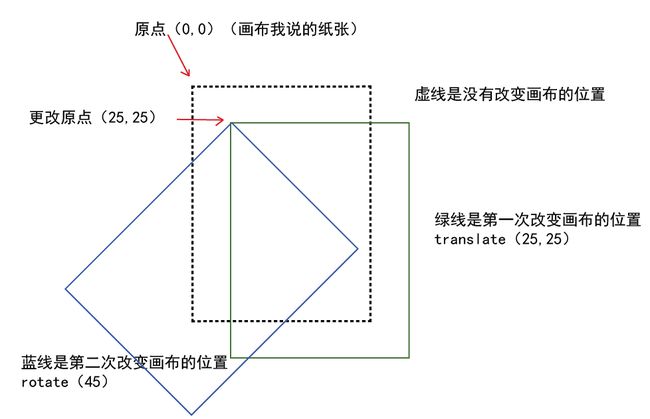
我在纸上画画,看看画布(纸张)的位置到底在发生什么变化:
ctx.translate(25,25);
接着:
ctx.rotate(45*Math.PI/180);
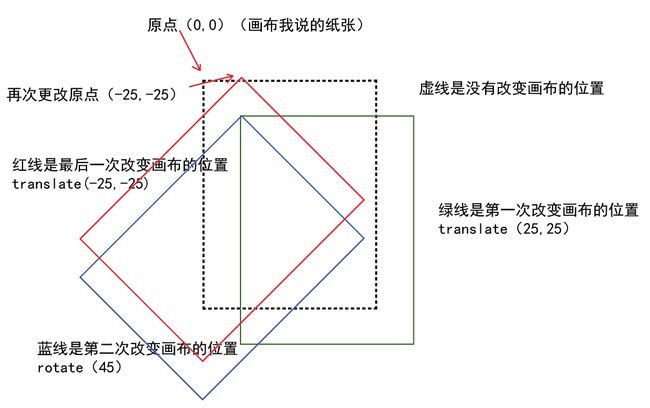
最后,我们调用了
ctx.translate(-25,-25);
红色框就是进行了三次变换后的画布的最后位置,那我们在上面要是画刚才的那个方块
drawRect(0,0,50,50);
那这个方块就正好是基于(25,25)点进行了一次旋转。
如果遇到ctx的位置变换,实在不明白就在脑子里想象出一张画布,然后每次变换后想一下它所在的位置,就好像我们的纸一样,我们在不停摆弄着它以便于我们绘制。
Context的scale
scale(缩放)是最好理解的,无非就是将坐标系拉伸或者缩小嘛。跟旋转一样的,缩放也是基于原点的哦。
比如:
let ctx = main.getContext('2d');
ctx.fillStyle = 'red';
ctx.globalAlpha = 0.5;
drawRect(0,0,50,50);
ctx.scale(1.5,1.5);
ctx.fillStyle = 'black';
drawRect(0,0,50,50);
function drawRect(x, y, width, height) {
ctx.beginPath();
ctx.rect(x, y, width, height);
ctx.closePath();
ctx.fill()
}
不用看结果,想都能想出来,有两个左上角坐标是0,0的方块,第二个比第一个大1.5倍,因为我们把坐标系放大了1.5倍。我这里用到了globalAlpha,让绘制的图形透明,这样好辨认
scale无非就是让坐标系进行缩放嘛,对不对。但是,一定要注意!一定要注意!一定要注意!scale并不是单纯的拉伸了长宽,而是让坐标系(看清楚是坐标系)整体发生了伸缩变化。啥意思啊,就是说如果我调用一次scale(2,2), 不是单纯理解为画布被放大了2倍,连坐标都放大了两倍(这么说有点不妥,但是好理解)。
上面那个case我们的方块坐标都是0,0,看不出来什么不一样,但如果我们把坐标改成50,50后会成这样:
let ctx = main.getContext('2d');
ctx.fillStyle = 'red';
ctx.globalAlpha = 0.5;
drawRect(50,50,50,50);
ctx.scale(1.5,1.5);
ctx.fillStyle = 'black';
drawRect(50,50,50,50);
function drawRect(x, y, width, height) {
ctx.beginPath();
ctx.rect(x, y, width, height);
ctx.closePath();
ctx.fill()
}
看到了吗,黑色方块的坐标并没有和红色方块的重合,就是因为整个坐标系都被放大了,在放大后的(50,50)和在放大之前的(50,50)并不一样。可以这么理解,原坐标也被放大了2倍,现在的50,50相当于以前的100,100
我先讲这么多,在后续会有更详细的说明。
Context的状态栈
状态这个东西不可能一直就这样变化下去,有时候我们只想局部发生变化,比如我画了一个黑色的方块,接着我想画一个旋转了45度的红色方块,最后我想在第一次绘制的黑色方块旁100像素位置再画一个黑色方块。
如果根据我们上面的代码,就这么写:
let ctx = main.getContext('2d');
ctx.fillStyle = 'black';
drawRect(50,50,50,50);
ctx.fillStyle = 'red';
ctx.rotate(45*Math.PI/180); // 顺时针旋转45
drawRect(50,50,50,50);
ctx.rotate(-45*Math.PI/180); // 逆时针旋转45,即回到刚才黑色方块的状态
ctx.fillStyle = 'black';
ctx.translate(100,0);
drawRect(50,50,50,50);
function drawRect(x, y, width, height) {
ctx.beginPath();
ctx.rect(x, y, width, height);
ctx.closePath();
ctx.fill()
}
看,在画完第二次后,为了让画布回到当初的状态,我不得不反向旋转一次。很sb吧。
ctx提供了两个方法,一个叫save,一个叫restore,save是保存当前状态,restore是恢复之前状态。
啥意思,就是说,我一旦调用save,那当前ctx的所有状态都会被保存起来,我可以任意修改,当我调用restore的话,就会把刚才保存的状态恢复。
这个是不是就是一个栈?我们模拟一下save和resotre,是这样的:
function save(){
stateStack.push(currentState.clone());
}
function restore(){
currentState = stateStack.pop();
}
get currentState(){
return stateStack[stateStack.length - 1]
}
一旦调用save,那ctx就会把当前状态克隆出来,压到栈中;那我们在绘制后续图形的时候,当前的状态随你怎么改都无所谓,反正被保存起来了,当我们调用restore,那当前的状态就恢复成了之前保存的状态。
所以,我刚才那段sb代码可以改成这样:
let ctx = main.getContext('2d');
ctx.fillStyle = 'black';
drawRect(50,50,50,50);
ctx.save();// 保存当前的状态
ctx.fillStyle = 'red';
ctx.rotate(45*Math.PI/180); // 顺时针旋转45
drawRect(50,50,50,50);
ctx.restore(); // 恢复之前状态(就是调用save前的状态)
ctx.translate(100,0);
drawRect(50,50,50,50);
切记,save和restore一般都是成对出现了,比如
ctx.save()
。。。// 做一些绘制操作
ctx.save();
。。。// 做另一些绘制操作
ctx.restore();
ctx.restore();
。。。// 再做一些操作
这样的话就不会造成一些莫名其妙的错误发生,你可以认为save和resotre相当于一段代码的{和},在括号内做你的操作,随便改状态,一旦出了括号,括号内你做的更改都没了。
状态栈很简单,知道Stack是什么就好理解它,我就不废话了。
小结
说到context的状态,实际上我主要还是讲了坐标变换而已,毕竟这个比起修改颜色啊,透明度要难一点,如果我把这些坐标变换的过程改到矩阵计算来说的话,就要更容易理解,我会在后期讲到webgl的时候再提及坐标的矩阵变换。
作业
上面我有个case:让某个方块根据它的中心点进行旋转,我也给出了代码,这个是有现实意义的,我们在移动端的旋转某图片的时候都是按照其中心旋转的。 那么,我要让某个方块根据它的中心进行伸缩呢?代码该怎么写?